【步态识别】MvGGAN 基于多视角步态生成对抗网络 算法学习《Multi-View Gait Image Generation for Cross-View Gait Recognition》

1. 论文&代码源

《Multi-View Gait Image Generation for Cross-View Gait Recognition》
论文地址：https://ieeexplore.ieee.org/document/9349211/
代码下载地址： 作者未提供源代码？

2. 论文亮点

在现实中难以在各种不同视角下捕捉步态数据，跨视角的步态识别是根据已知试图的步态数据识别未知视图下的步态数据。
跨视角的步态识别方法主要有两种：视角转换模型（VTM）和视角不变特征提取。
视角转换模型（View Transformation Model）的基础是奇异值分解（SVD），相关内容参见知识补充部分。

1. 不同视角下的步态图像由单一生成器自动生成。可以利用不同受试者和不同数据集共同提取步态特征，还可以使单一生成器学习到不同受试者和数据集更丰富的步态信息，增加假样本的多样性。
2. 对真假步态样本进行基于投影最大平均差异（MMD）的域对齐，减少假样本生成过程产生的域转移带来的影响。
3. 添加相同或不同数据集生成的假样本扩展数据集，提高步态分类模型的泛化能力。
   

3. 多视角的生成对抗网络

3.1 网络生成历程

当生成器接受图像作为输入时，生成器可以将输入图像转移到目标图像定义的域中，实现域的转移任务。给定成对的样本，域的转移任务可以通过监督学习的方式实现（如pix2pix方法）。
（问题1）但步态图像是离散的，不同视角下很难实现无偏差对齐，因此基于非配对的无监督GANs更加适用。
在某一视角下，$\mathbf{U}\to \mathbf{V}$需构建$G_A,D_A$；$\mathbf{V}\to \mathbf{U}$需构建$G_B,D_B$，假设有$k$个视角，则需要训练$k(k-1)$次。
这里不太明白
（问题2）当数据量较少时，难以训练多个GANs，从而容易出现过拟合现象，所以作者提出了训练一个以目标视图标签为条件的条件GAN来控制生成步态图像的视图的单一生成器G，实现多视角映射，MvGGAN具体工作原理如下：
（引出此方法）
$$\{\begin{array}{l}给定输入图像序列X=\{x_1,x_2,...,x_N\}，目标视角标签c\\ 由G(X,v)\to Y得到输出图像序列Y=\{y_1,y_2,...,y_N\}\\ 判别器预测输出图像视角和身份的真假\end{array}$$
$MvGGAN$类似$StarGAN$，区别在于：

StarGAN	MvGGAN
将图像从一个域转换到另一个域，不需要保留身份信息	生成更多的多域多样的假样本，需要保留身份信息作为训练数据

3.2 网络结构

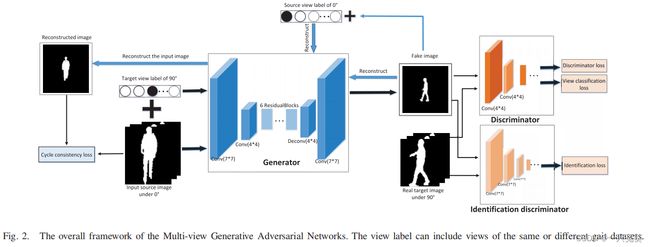
上图中的角度仅是示意作用。生成器共有2个初始输入量：原始步态图像（$0°$）、目标步态角度（$90°$），这两个输入量将输出一组角度为$90°$的假图像（Fake image）；还有2个过程输入量：原始步态角度（$0°$）、假图像（$90°$），这两个输入量将输出一组角度为$0°$重建图像（Reconstructed image）（假中假）。
角度均为$90°$的真假图像输入判别器（Discriminator）和识别判别器（Identification discriminator），分别计算判别损失、视角分类损失和判别损失。

3.3 损失函数

3.3.1 判别器损失（Discriminator Loss）

我们需要判断生成器输出图像的真假概率，判别器尝试去区分出假的图像，生成器则去尽力“欺骗”判别器，这样在判别器上的对抗损失函数如下：
$$L_{adv}={\mathbb{E}}_X[\log D(X)]+{\mathbb{E}}_{X,v_t}[\log (1-D(G(X,v_t)))](1)$$
其中，$G(X,v_t)$表示输入图像序列$X$基于视角$v_t$在生成器中进行生成。

3.3.2 视角分类损失（View Classification Loss）

为了生成特定视角$v_t$下的步态图像，需要通过视角分类网络将生成的步态样本归入相应的视角$v_t$中。假设有$k$个视角，在判别器$D$上增加一个具有$k$个输出节点的分类器实现视角的分类。视角分类网络表示为$D_{view}$，首先需要对$D_{view}$进行优化，将真实的步态图像作为输入，相应的真实的视角标签作为输出，优化过程的损失函数如下：
$$L_{view}^{real}={\mathbb{E}}_{X,v_t}[\log D_{view}(v_t|X)]$$
其中，$D_{view}(v_t|X)$表示输入图像$X$属于视角$v_t$的可能性（概率值）。这个损失是负值？
此网络还用于将$G$生成的假图像正确地分类到目标视角$v_t$中，因此$G$需要最小化以下损失函数：
$$\begin{gathered} L_{view}^{fake}={\mathbb{E}}_{X,v_t}[-\log D_{view}(v_t|Y)] \\ ={\mathbb{E}}_{X,v_t}[-\log D_{view}(v_t|G(X,v_t))](2) \end{gathered}$$

3.3.3 循环一致性损失（Cycle Consistency Loss）

前面两种损失的衡量目的是为了生成看起来更为真实且属于目标视角的步态图像，但是除了视角变化外，还可能存在其他方面的变化（如：着装、携带物等），这样会使得生成结果变得难以控制。为了保留输入步态样本的其他步态信息，同时只改变视角单一元素，此处引入循环一致性损失函数，以尽可能地保留视角变化之外的步态信息。
$$L_{rec}={\mathbb{E}}_{X,v,v_t}[||X-G(G(X,v_t),v)|{|}_1](3)$$
其中，生成器$G$被使用了两次，一次是$G(X,v_t)$生成视角$v_t$下的（假）步态图像，另一次是$G(G(X,v_t),v)$重建视角$v$下的原始输入序列。

3.3.4 识别损失（Identification Loss）

重建损失试图保留输入序列中每一个步态图像的结构信息以及视角信息，但是这种损失的构建是将每一个步态图像分别进行处理的，并没有考虑不同图像帧之间的关系。实际情况是，步态是一连串帧组成的动态信息，逐帧计算损失可能会导致主体识别失误。因此需要设计一个识别判别器$D_{id}$。识别判别器将原始步态数据序列和生成器输出的步态图像序列作为一个训练数据对，并产生该数据对是否来自同一个人的概率，如果来自同一主体，则输出为$1$，否则输出$0$，损失函数如下：
$$L_{id}={\mathbb{E}}_X[\log D_{id}(X)]+v{\mathbb{E}}_{X,v_t}[\log (1-D_{id}(G(X,v_t)))](4)$$
为了充分利用动静态的步态信息，文章设计了基于$LB$网络的识别判别器结构。

3.3.5 完整目标损失函数（Full Objective）

结合以上4个损失函数，可以得到最终的目标损失函数：
$$L(G,D)=L_{adv}+{\lambda }_{view}{L}_{view}^{real}+{\lambda }_{view}{L}_{view}^{fake}+{\lambda }_{rec}{L}_{rec}+{\lambda }_{id}{L}_{id}(5)$$
其中，$G$试图最小化这个目标损失，而$D$则试图将其最大化，$\lambda$是超参数（机器学习模型里面的框架参数），用于控制不同损失函数在优化过程中的重要性（权重占比）。

3.4 其他细节分析

3.4.1 跨数据集的多视角生成

通过控制视角标签向量$v_t$来控制生成步态图像的目标视角，如果$v_t$由来自包括$k_1$个视角的数据集$A$组成，那么就可以在$k_1$个视角下生成步态样本。此外，将包括$k_2$个视角的数据集$B$与$v_t$结合起来，那么$MvGGAN$就可以在$k_1+k_2$个视角下生成步态样本。通过这种方式，数据集$A$和数据集$B$都将包括$k_1+k_2$个视角，两个数据集都被扩展到包含更多的样本。
为了实现上述文字所描述的目标，作者依据$StarGAN$方法，定义了一个统一的标签向量$\tilde{v}$：
$$\tilde{v}=[v_1,...,v_n,m](6)$$
其中，$v_i$表示的是数据集中第$i$个向量标签，$m$是一个$n$维的独热向量，如果$m$的第$i$个元素是$1$，说明生成的步态图像的目标视角是第$i$个。

3.4.2 多数据集训练

在步态识别中，除了视角差异，着装和携带物也是两个十分重要的影响因素，因此作者假设同一个着装条件或相同携带物的步态样本作为同一个“域”，前面提到$k$代表数据集中有$k$个视角标签，整体是一个$k$维的独热向量。现在需要将代表着装或携带物属性的标签与$k$进行串联，形成一个统一的标签向量$u$，有$u=[k,d]$，其中$d$代表着装或携带物条件的独热向量。
在现实生活中，着装和携带物的变化是多种多样的，从而应当对应不同的域，但是实验过程中难以实现，所以作者仅针对CASIA-B数据集涉及的两种典型着装（夏装和大衣），以及两种典型携带物（双肩包和单肩包）进行实验。
在实验过程中，将“nm”、“bg”和“cl”类型视为三个域。

3.4.3 真假步态图像之间数据集的适应性

由于作者使用的是单一生成器来生成不同行走条件下（甚至不同数据集）的假步态图像，理论上，真假步态图像之间应该存在分布差异，因此，作者使用t-SNE方法将真假步态图像的分布进行可视化操作，如下图所示：

标签0-4为假步态图像，5-9为真步态图像。左图中的假步态图像涵盖了来自CASIA-B和OU-MVLP数据集的22个不同的视角，真步态图像仅涵盖来自CASIA-B的11个不同的视角；右图仅显示在90°视角下的真假步态图像，不难看出二者在分布上存在明显的差异。
为了解决上述问题，作者引入域对齐方法，学习一个特征映射函数$F(\cdot )$以减少真假步态图像的分布差异。真步态特征集合为${\mathcal{D}}_r=\{{\mathbf{x}}_{r_i},y_{r_i}{\}}_{i=1}^n$，假步态特征集合为${\mathcal{D}}_f=\{{\mathbf{x}}_{f_j},y_{f_j}{\}}_{j=n+1}^{n+m}$，以及标签空间${\mathcal{Y}}_r={\mathcal{Y}}_f$。不同数据集之间的分布差异由边际分布（P）主导，同一数据集的样本分布差异由条件分布（Q）主导，考虑这两方面因素，作者提出：
$$D_F({\mathcal{D}}_r,{\mathcal{D}}_f)=(1-\eta )D_F(P_r,P_f)+\eta \sum _{c=1}^C{D}_F^{(c)}(Q_r,Q_f)(7)$$
其中，$\eta$是平衡边际分布和条件分布的自适应因子；$c\in 1,...,C$表示步态图像主体的ID，$D_F(P_r,P_f)$为边际分布排列，$D_F^{(c)}(Q_r,Q_f)$是ID为$c$的条件分布排列。
真假步态图像之间的分布差异可以通过最大平均值差异（Maximum Mean Discrepancy, MMD） 来进行计算，具体计算公式为：
$$\begin{gathered} D_F({\mathcal{D}}_r,{\mathcal{D}}_f)=(1-\eta )||\mathbb{E}[F({\mathbf{x}}_r)]-\mathbb{E}[F({\mathbf{x}}_f)]|{|}_{{\mathcal{H}}_K}^2 \\ +\eta \sum _{c=1}^C||\mathbb{E}[F({\mathbf{x}}_r^{(c)})]-\mathbb{E}[F({\mathbf{x}}_f^{(c)})]|{|}_{{\mathcal{H}}_K}^2(8) \end{gathered}$$
其中，$\mathbb{E}[\cdot ]$是嵌入特征的均值；${\mathcal{H}}_K$表示的是再生核希伯尔特空间（Reproducing Kernel Hilbert Space, RKHS），基于表示定理（Representer Theorem），公式$(8)$可以表示为
$$D_F({\mathcal{D}}_r,{\mathcal{D}}_f)=\text{tr}({\mathbf{F}}^T\mathbf{M}\mathbf{F})(9)$$
其中，$\mathcal{F}\in {\mathbb{R}}^{(n+m)\times d}$是每个样本的特征向量连接成的特征矩阵，在特征矩阵中每一行代表真假样本$\mathbf{x}$的特征向量$F(\mathbf{x})$，$d$是特征向量$F(\mathbf{x})$的维度。
MMD的矩阵$\mathbf{M}=(1-\eta ){\mathbf{M}}_0+\eta {\sum }_{c=1}^C{\mathbf{M}}_c(10)$用于计算矩阵$\mathbf{F}$中步态特征的分布差异（distribution divergence），公式$(10)$中各元素的计算式如下：
$$({\mathbf{M}}_0{)}_{ij}=\{\begin{array}{ll}\frac{1}{n^2},& {\mathbf{x}}_i,{\mathbf{x}}_j\in {\mathcal{D}}_r\\ \frac{1}{m^2},& {\mathbf{x}}_i,{\mathbf{x}}_j\in {\mathcal{D}}_j\\ -\frac{1}{mn},& \text{others}\end{array}(11)$$
$$({\mathbf{M}}_c{)}_{ij}=\{\begin{array}{ll}\frac{1}{n_c^2},& {\mathbf{x}}_i,{\mathbf{x}}_j\in {\mathcal{D}}_r^{(c)}\\ \frac{1}{m_c^2},& {\mathbf{x}}_i,{\mathbf{x}}_j\in {\mathcal{D}}_j^{(c)}\\ -\frac{1}{m_c{n}_c},& {\mathbf{x}}_i\in D_r^{(c)},{\mathbf{x}}_j\in {\mathcal{D}}_f^{(c)}or{\mathbf{x}}_i\in D_f^{(c)},{\mathbf{x}}_j\in {\mathcal{D}}_r^{(c)}\\ 0,& \text{others}\end{array}(12)$$
其中$n_c$，$m_c$分别表示受试者$c$的真假样本数量。实验中，对于同一数据集生成的假步态样本，设置$\eta =0.8$，跨数据集生成的假步态样本，设置$\eta =0.2$。

为了减少真假样本的分布差异，映射函数$F$在训练过程中需要最小化公式$(7)$中的目标函数。在本文中，映射函数$F$被构建为一个多层全连接网络——输入的步态特征可以从步态分类网络的任何一层提取。作者将中间层的节点数设为为1024，原因是：域对齐网络的目的是减少真假步态图像之间的分布差异，也就是说，我们只要求真假图像的整体分布一致，单幅图像的合并特征不受约束，实验发现中间层1024个节点数足以实现分布对齐。更多的节点数会增加计算成本和过拟合风险，并且不会带来性能的提高。对齐后的步态特征被输入到步态分类网络的下一层，完成训练或测试。

3.5 实验实施

3.5.1 网络结构

生成器参考StarGAN模型，判别器使用PatchGAN模型，判别损失采用【A comprehensive study on cross-view gait based human identification with deep CNN】文章中的LB网络。

3.5.2 训练过程

在损失函数${\mathcal{L}}_{adv}$中采用Wasserstein GAN（WGAN），来稳定对抗性训练过程。
超参数设置${\lambda }_{view}=1$，${\lambda }_{rec}=10$，${\lambda }_{id}=5$，使用Adam优化生成器和判别器。batch size为$16$，判别器每更新五次，生成器更新一次。学习率初值为$0.0001$，epoch值为$50$，学习率会随着迭代线性衰减到$0$。

4. 实验结果

5. 总结

在本文中，作者基于多视角步态生成对抗网络（MvGGAN），在不同的步态数据集下生成不同视角的假步态样本。MvGGAN包括一个生成器和一个判别器，前者在几种行走条件下生成假步态样本，后者实现了对抗性训练并保留了人的身份信息。通过向原始步态数据集添加生成的假步态样本，并在真实样本和假样本之间进行域对齐操作，使得基于深度学习的步态分类网络的性能可以得到明显改善。

本文证明了通过向原始步态数据集添加假样本，来提高跨视角步态识别性能是切实可行的，同时也证明了在一个数据集的不同视角或其他行走条件下为另一个数据集生成假样本同样可行。跨数据集的步态图像生成相当重要，因为它可以使步态分类网络在尽可能多的行走条件下学习步态信息，并提高现实场景中（含有大量未登记的步态样本）步态识别的性能。

0. 知识补充

0.1 奇异值分解（SVD）

奇异值分解(Singular Value Decomposition)是在机器学习领域广泛应用的算法，不仅可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域，是很多机器学习算法实现的基础。

特征值和特征向量
$$Aw=\lambda w$$
其中，$A$是$n\times n$维的矩阵，$w$是一个$n$维向量（特征向量），$\lambda$是与特征向量$w$相对应的特征值。
特征值和特征向量求出后，可以将矩阵$A$进行特征分解：
$$A=W\Sigma W^{-1}$$
其中，$W$是由$n$个特征向量$w_1,w_2,...,w_n$组成的$n\times n$维矩阵，$\Sigma$是由特征向量$w_i$对应的特征值${\lambda }_i$在主对角线上组成的对角阵。
若$A$不是$n\times n$维的方阵，而是行列数不相同的$m\times n$维矩阵，那么就需要进行奇异值分解。

SVD
$$A=U\Sigma V^T$$
其中，$U\in {\mathbf{R}}^{m\times m}$，$\Sigma \in {\mathbf{R}}^{m\times n}$，$V\in {\mathbf{R}}^{n\times n}$，$\Sigma$除主对角线上的元素以外均为$0$，主对角线上的元素即为奇异值，$U$和$V$均为正定矩阵（酉矩阵），满足$U^{T}U=I,V^{T}V=I$。
对矩阵的转置$A^T$和矩阵$A$做乘法，得到一个$n\times n$维的方阵，对这一方阵进行特征分解，得到特征值和特征向量满足下式：
$$(A^{T}A)v_i=\lambda v_i$$
其中，由特征向量$v_i$组成的矩阵$V$就是奇异值分解公式中的$V$；同理，
$$(A{A}^T)u_i=\lambda u_i$$
一般将矩阵$U$成为左奇异向量。
接下来求解$\Sigma$矩阵。
$$\begin{gathered} A=U\Sigma V^T\to AV=U\Sigma V^{T}V=U\Sigma \\ \to A{v}_i=u_i{\sigma }_i \\ \to {\sigma }_i=\frac{A{v}_i}{u_i} \end{gathered}$$
经过以上推导，就可以求出各个奇异值${\sigma }_i$，从而求出$\Sigma$矩阵。
此外，还有一种求解$\Sigma$矩阵的方法，就是从前面定义$(A^{T}A)$的特征矩阵是$V$，$(A{A}^T)$的特征矩阵是$U$，这一点入手。以$V$矩阵为例：
$$\begin{gathered} A=U\Sigma V^T \\ \to A^T=(U\Sigma V^T{)}^T=V\Sigma U^T \\ \to A^{T}A=(V\Sigma U^T)(U\Sigma V^T)=V{\Sigma }^2{V}^T \end{gathered}$$
上面的推导过程说明$A^{T}A$的特征向量组成的矩阵就是$V$，而且特征值矩阵是奇异值矩阵的平方，即
$${\sigma }_i={\sqrt{\lambda }}_i$$

0.2 生成对抗网络（GAN）

0.2.1 基本概念

生成对抗网络（Generate Adversarial Networks）是一种生成模型，主要由判别器和生成器两部分构成。
判别器（discriminator）： 数学表示为$y=f(x)$或条件概率分布$p(y|x)$。当输入训练集图片为$x$时，判别器输出分类标签$y$，学习的是输入图片$x$与输出标签$y$的映射关系。
生成器（generator）： 数学表示为概率分布$p(x)$。没有约束条件的生成器是一种无监督模型，将给定的简单先验分布$\pi (z)$（通常是高斯分布）映射为训练集图片的像素概率分布$p(x)$，即输出一张服从$p(x)$分布的具有训练集特征的图片。

0.2.2 其他生成网络

1. 自回归模型（AutoRegressive model, AR）
2. 变分自编码器（Variational AutoEncoder, VAE）
3. 基于流的生成模型（Flow-based generator model）

0.2.3 损失函数

$$L=\min \max V(D,G)={\mathbf{E}}_{x\sim p_{data}(x)}[logD(x)]+{\mathbf{E}}_{Z\sim p_z(x)}[log(1-D(z))]$$
逐层来看
$V(D,G)$是生成（假）样本和真实样本的差异；
$\max V(D,G)$生成器固定，最大化交叉熵损失，更新判别器；
$\min \max V(D,G)$生成器在最大化交叉熵损失的前提下，最小化这个损失。

0.2.4 训练流程

先训练判别器
将训练集数据（training set）打上真标签，生成器生成的假图片（fake image）打上假标签，二者组成batch送入判别器进行训练。计算loss时，使判别器对training set判别趋近于真，fake image趋近于假，此过程只更新判别器参数。
再训练生成器
将高斯分布噪声$z$（random noise）送入生成器，将生成器生成的fake image打上真标签送入判别器，计算loss时，使判别器对fake image判别趋近于真，此过程只更新生成器参数。

0.3 t-SNE

t-SNE的主要用途是可视化和探索高维数据。 它由Laurens van der Maatens和Geoffrey Hinton在JMLR第九卷(2008年)中开发并出版。 t-SNE的主要目标是将多维数据集转换为低维数据集。 相对于其他的降维算法，对于数据可视化而言t-SNE的效果最好。 如果我们将t-SNE应用于n维数据，它将智能地将n维数据映射到3d甚至2d数据，并且原始数据的相对相似性非常好。与PCA一样，t-SNE不是线性降维技术，它遵循非线性，这是它可以捕获高维数据的复杂流形结构的主要原因。

参考博客：

生成对抗网络GAN损失函数loss的简单理解

GAN的Loss的比较研究（1）——传统GAN的Loss的理解1

奇异值分解

奇异值分解（SVD）原理与在降维中的应用

矩阵的奇异值与特征值有什么相似之处与区别之处

t-SNE：可视化效果最好的降维算法