核磁共振重建算法综述
自己整理的一些核磁共振重建综述文章,仅供参考,不发表~
文章目录
- 摘要
- 一、引言
- 二、核磁共振成像原理
-
- 2.1.核磁共振成像过程
- 2.2.K空间
- 2.3.核磁共振数据采集过程
- 三 核磁共振重建方法
-
- 3.1.部分傅里叶重建方法
- 3.2.并行重建方法
-
- 3.2.1 常用的并行重建方法
- 3.2.2 同时多层重建方法
- 3.2.3 三维并行成像
- 3.3.压缩感知重建方法
-
- 3.3.1 压缩感知原理
- 3.3.2 压缩感知重建过程
- 3.4.基于深度学习的MRI重建方法
-
- 3.4.1 基于数据驱动的深度学习重建方法
- 3.4.1 基于物理原理的深度学习重建方法
- 四、总结
- 参考文献
摘要
摘要:当前,核磁共振成像在临床上应用十分广泛,而核磁共振重建方法在核磁共振成像过程中至关重要。本报告将首先简要介绍了核磁共振成像原理;然后,从时间维度和技术维度重点介绍四大类核磁共振重建方法的发展之路,包括部分傅立叶重建方法、并行成像重建方法、压缩感知重建方法和基于深度学习的重建方法。具体地,对于部分傅里叶重建方法,本报告将涉及零填充、共轭对称、Homodyne等多个方法;对于并行成像方法,本报告将涉及SENSE、GRAPPA和SPIRiT等临床实践中最常用的重建技术;对于压缩感知重建方,本报告介绍压缩感知重建的原理以及在核磁共振重建中的应用;对于深度学习重建方法,本报告主要介绍了基于数据驱动的端到端的深度学习重建方法和基于核磁物理成像原理的深度学习重建这两大类方法。最后指出在深度学习背景下当前核磁共振重建的研究热点和未来发展趋势。
关键词:深度学习、核磁共振重建方法、MRI、并行成像、压缩感知、部分傅里叶
一、引言
核磁共振成像(MRI)具有无辐射、高分辨率、多对比度等优点,广泛应用于医学成像,已经成为一种重要的临床医学检查手段,为临床影像诊断提供了非常有价值的信息。
但是与其他的成像方法相比,MRI需要较长的扫描时间。MRI信号的空间定位是导致扫描时间长的主要原因之一。每个脉冲序列需要多次经历射频激发、梯度编码和数据采集这几个步骤才能生成图像。获取一副MRI图像所需的时间最少需要数百毫秒,如快速梯度回波或回波平面成像(EPI)等,有的序列成像甚至需要几分钟,如自旋回波和扩散加权序列[1]。而且,MRI扫描时间过长,成像缓慢,会给患者带来不适。此外,患者的器官运动,如呼吸、吞咽和自然心跳,会导致图像模糊和对比度失真,无法满足实时动态高精度成像的要求,影响MRI的进一步推广与发展。
本报告主要总结了MRI重建的关键进展和发展历程,因为图像重建方法可用于减少扫描时间,从而提高空间分辨率和成像质量,同时也可以减少患者的不适。目前,MRI重建主要包括四大类,部分傅立叶重建方法、并行成像重建方法、压缩感知重建方法和基于深度学习的重建方法。
本报告将首先简要介绍核磁共振成像原理,主要包括核磁共振成像的基本概念、K空间的概念、核磁共振数据的采集的原理。然后回顾核磁共振重建方法的发展历程并依次介绍MRI重建的四大类,先介绍了最早的核磁共振的重建方法即部分傅里叶重建重建方法,部分傅里叶重建算法主要介绍了零填充、共轭对称、Homodyne等,部分傅里叶变换的算法过程比较缓慢,重建效果不太好,伪影比较严重,图像质量一般,在临床的应用极少。然后,重点介绍了并行成像方法,并行成像方法是目前在临床应用中最广泛的重建方法。并行成像技术主要分为两类,一类是在图像域来分离混叠的伪影,主要代表算法是SENSE和PILS等;另外一类是在K空间解混叠,然后在通过反傅里叶变换到图像域,这类并行成像的代表算法是SAMSH等。SPIRiT及其扩展算法也是常用的典型的并行成像方法。本文将主要SENSE、GRAPPA和SPIRiT方法,因为它们是在临床实践中最常用的重建技术。然后,介绍了一些同时多层重建方法和三维的并行成像方法。接着,介绍了压缩感知的基本原理,和基于压缩感知的重建方法,以及一些和并行成像结合的压缩感知重建方法。最后介绍了基于深度学习的重建方法,主要包括两类:基于数据驱动的端到端的深度学习重建方法和基于核磁物理成像原理的深度学习重建方法。基于数据驱动的端到端的深度学习重建方法中主要介绍了基于卷积神经网络CNN和深度级联网络的重建方法,基于核磁物理成像原理的深度学习重建方法主要介绍了基于变分网络和基于物理方法的无监督重建方法。
最后,总结了核磁共振重建方法最新的进展,并指出在深度学习背景下核磁共振重建的研究热点和未来发展趋势。
二、核磁共振成像原理
在磁共振成像中,我们会首先利用射频脉冲RF激发成像区域,利用梯度场的产生及切换来进行每个质子的空间定位,再利用采集信号系统来采集磁共振信号,最后使用傅里叶变换及后处理等重建系统来重建图像。
2.1.核磁共振成像过程
核磁共振基本仪器的简化图如图1所示,仪器周围是线圈,包括主线圈B0、梯度线圈和射频场线圈,梯度线圈由x,y和z三个线圈组成,图中只显示了两个。该系统的主要硬件是一个大磁铁,提供稳定、均匀的场B0,范围通常在0.1-3.0 T。对于临床使用,磁铁必须有一个足够大的孔,以允许人体躯干进入。目前使用的磁体有三种:永磁体、阻性磁体(空芯或铁芯)和超导磁体。它们在成本、重量、场强、稳定性、均匀性和边缘场等方面各有优缺点。最受欢迎的磁体类型是超导磁体,主要是因为它具有优良的均匀性、稳定性和较高的场强。然而,超导磁体需要低温(液氦),价格更贵,并且会产生可以延伸很长的距离的边缘场,这使得磁体的选择更具挑战性。
主线圈用来产生一个强大的静磁场,射频线圈用来发射射频(RF)信号并接收从被检测者发出的用于成像的射频信号,梯度线圈中的三个线圈分别用来控制频率编码信息、相位编码信息和断层选择信息。最后将采集到射频信号送入数据处理系统,信号经过数据处理后形成一幅对我们有用的核磁共振图像。

图1 MRI基本仪器的简化图
核磁共振是一种在稳定磁场中处于自旋状态的氢原子在遇到交变磁场时发生的现象[2]。当被检测者处于MRI设备中时,人体中的氢原子会在主磁体产生的磁场中旋转。当RF线圈发出频率为Larmor的交变电磁场时,它处于自旋状态。氢原子被激发,氢原子核吸收一定的能量而共振。受激的氢原子围绕主磁体的磁场产生进动。当射频脉冲停止时,激发的氢原子核逐渐释放吸收的能量,其相位和能级恢复到激发前的状态。这个恢复过程称为弛豫过程,回到原来的平衡状态需要的时间称为弛豫时间。在此过程中,通过调节梯度线圈对人体的射频信号进行频率和相位编码,并由射频线圈记录。
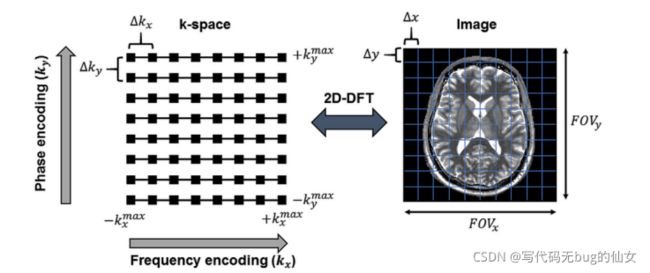
2.2.K空间
磁共振图像的采样不同于其他医学图像的采样,其他医学图像在像素域采样,而它的原始数据是在图像的频域内进行采样,即在K空间采集数据。由这些梯度磁场产生的原始MRI数据形成了一个空间频率矩阵,这个矩阵被称为K空间,对K空间可以用二维离散傅里叶来生成MRI图像。K空间的概念对于研究磁共振MRI重建问题至关重要,为后续图像重建算法打下理论基础。在介绍K空间之前,我们先介绍一下MR信号的的信号方程式,来描述MR图像形成的基本原理。设m(x, y)为我们需要重构的图像,m(x, y)是一个复值图像

根据以上,我们可以知道,核磁共振成像的目标便是重构m(x, y),以及将|m(x, y)|显示出来。设x,y线圈的梯度分别为Gx,Gy,则核磁共振设备采集到的信号的方程[11]为

由信号方程可以知道,K空间是带有空间位置信息编码的磁共振数据,也是图像的傅里叶空间。想要重建原图像m(x, y),只需要将原始K空间的采样点进行逆傅里叶转换,即将具有不同频率编码信息和相位编码信息的核磁共振信号的能量聚焦到相应的位置,就可以得到我们看到的核磁共振图像。
2.3.核磁共振数据采集过程
如图2所示,所需的空间分辨率和视野(FOV)决定了应获得多少K空间数据,相邻k个空间线之间的间距与FOV成反比:
要在一个方向增加FOV,在k空间采样的间距必须减小。奈奎斯特采样定理指出,FOV应该大于成像的对象的大小,以避免混叠。如果不满足此条件,高频信号将错误地显示为低频率信号。由于频率信息用于确定空间位置,因此会将FOV外部的对象的图像的叠加在FOV内部对象的图像的信号上,产生混叠伪影。
空间分辨率与原点到k空间最大距离(kmax)成反比:

通常,k空间的数据是在笛卡尔网格上采样得到的,每一次重复时间(TR)采集一条相位编码(ky)线。总采集时间(TA)由TR、采集的相位编码线数(Ny)和信号平均数(NA)确定
![]()
从上述方程可以知道,有两种减少总扫描时间的方法。首先,可以缩短TR。然而,TR影响图像对比度,并受到用于成像的脉冲序列类型的限制。另一个方法是减少采集的相位编码线数(Ny),对K空间进行欠采样,图3是不同的K空间轨迹及其相关的混叠伪影的例子。采集的k空间数据用实线表示,而缺失的数据用虚线表示,(a)全采样的笛卡尔数据会产生一个完整的FOV图像。(b)加速度因子为R=3的均匀笛卡尔k空间会导致相干混叠伪影。© 可变密度采样,在k空间中心附近采集更多数据,成像伪影更分散。(d)径向欠采样每隔固定角度径向采样一次,生成了漫射条纹伪影。(e)螺旋k空间采样,产生不相干的旋转伪影。
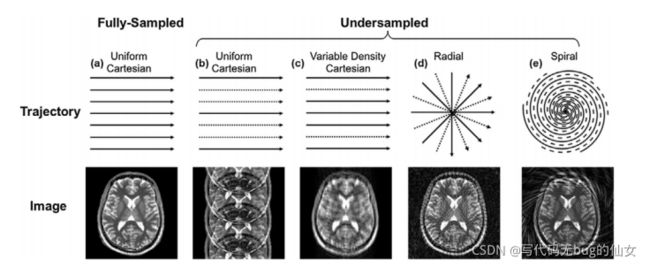
核磁共振扫描采集的数据是K空间数据,也就是频域数据,通过傅里叶变换可以得到图像域数据。重建就是把k空间数据转换为图像域数据的过程。各种MRI重建方法的目标是利用欠采样的K空间数据重建出高质量的MRI图像。目前已经产生了许多不同的重建方法,它们基本原理相似,将在下文中将一一叙述。
三 核磁共振重建方法
3.1.部分傅里叶重建方法
部分傅里叶成像算法是最早的基于K空间的信号采集方法,它利用K空间的共轭对称性,采集 50% 以上的数据,再利用各种算法对未采集的数据进行填补,从而大量缩短扫描时间。部分傅里叶重建算法主要包括零填充、共轭对称、Homodyne等[3],各种算法的目的都是实现相位校正。这是由于在 MRI设备中,采样时的运动、共振频率偏移、硬件延迟、涡流、磁场非均匀性等原因会造成数据的非完全对称,共轭对称的数据会引入相位错误。这些重建算法在数据的非均匀性增加的时候,越发显现其重要性。
零填充是最简单的重建方法,即对K空间未采集的数据采用0来填充,再进行傅里叶变换;共轭填充利用厄米(hermitian)对称性,共轭填充K空间未采集的数据,即对一定层面S(-kx,-ky)=S*(kx,ky);Homodyne算法填充将数据分为对称部分和非对称部分分别进行处理,并进行相位矫正。对称部分为相位变化的低频部分,非对称部分为相位变化的高频部分。
部分傅里叶变换的算法过程比较缓慢,重建效果不太好,伪影比较严重,图像质量一般,在临床的应用极少。
3.2.并行重建方法
并行成像方法是目前在核磁共振扫描仪中应用最广泛的重建方法。并行成像利用一组射频接收线圈阵列的空间信息来代替常规需要梯度磁场才能提供的信息,即利用在空间位置上,相控阵线圈灵敏度的差异进行空间编码,代替一部分梯度编码,从而减少K空间数据采集,来减少成像时间[2]。并行成像的目标是消除由于k空间中的相位编码线采样不足而导致的混叠伪影。
3.2.1 常用的并行重建方法
并行成像技术主要分为两类,一类是在图像域来分离混叠的伪影,主要代表算法是SENSE(1999年)[4],PILS(2000年)[5]等;另外一类是在K空间解混叠,然后在通过反傅里叶变换到图像域,这类并行成像的代表算法是SAMSH(1997年)[6],AUTO-SMASH(1998年)[7],VD-AUTO-SMASH(2001年)[8]和GRAPPA(2002年)[9]。SPIRiT(2010)[10]及其扩展算法ESPIRiT (2014年)[11]和l1-SPIRiT (2012年)[12]也是常用的典型的并行成像方法。接下来将简介SENSE、GRAPPA和SPIRiT方法,因为它们是在临床实践中最常用的重建技术。
(1) SENSE重建方法
灵敏度编码(sensitivity encoding, SENSE)是一种技术图像域的重建方法,SENSE方法采用多个接收线圈用于信号采集,允许对K空间欠采样。欠采样的过程中会丢失一些空间编码信息,所以SENSE重建时,利用各个线圈的空间灵敏度对丢失的信息进行恢复,将混叠的图像进行展开,得到没有伪影的图像。SENSE重建可以减少K空间采集线数,缩短扫描时间。但是由于欠采样导致图像信噪比降低;而且SENSE重建需要估计线圈敏感度信息,重建过程比较麻烦;且线圈敏感度信息很难准确估计,其误差会导致重建图像伪影。
(2) GRAPPA重建方法
GRAPPA技术(Generalized autocalibrating partially parallel acquisitions )是一种基于 K空间的重建算法,它以满足奈奎斯特采样定律要求的频率采集K空间中心数据作为自动校正数据(Auto-Calibration Signal, ACS),利用多通道K空间相邻的点线性相关性进行每个通道的K空间欠采样的填充,得到每个通道的全K空间,最后通过通道融合(SOS or ACC)得到最终的无卷褶图像。
(3) SPIRiT重建方法
SPIRiT技术(iterative self-consistent parallel imaging reconstruction from arbitrary k-space)结合了SENSE和GRAPPA的特征。和GRAPPA一样,SPIRiT利用相邻的k空间数据之间的相关性来恢复丢失的信息。但是和SENSE一样,重建被构造为一个逆问题。无论原始的采样轨迹如何,SPIRiT的输出都是一个笛卡尔K空间。SPIRiT重建通常用零填充和欠采样的K空间进行初始化,并作为一个优化问题进行迭代求解。在每次迭代中,算法转向最小化和平衡两个项之间的误差:校准一致性和数据一致性。
3.2.2 同时多层重建方法
前一部分已经描述了减少生成二维图像所需的相位编码数的一些并行成像方法。这些方法充分利用了扫描平面内的线圈灵敏度信息。然而,并行成像也可以用来分离有混叠切片,达到在获取一个切片的时间内成像几个切片的目的。这些同时的多切片技术利用了在切片编码方向上的线圈灵敏度的差异,但依然基于上述方法中相同的并行成像原理。
SMS(Simultaneous multi-slice imaging)[13]技术使用多频带射频脉冲[92,93]同时激发几个切片。类似于加速度因子,同时获得的切片数称为多带因子(MB)。多波段脉冲由一对以不同频带为中心的射频波形组成。复合脉冲采用切片选择梯度,以激发多个频带,从而激发多个切片。需要注意不能超过射频放大器的特定吸收率(SAR)限制或电压限制。当将SMS与自旋回波等高能脉冲序列相结合时,SAR值是值得关注的一个问题。
3.2.3 三维并行成像
前面讨论的许多技术已经被推广到加速三维的并行成像中。多层的MRI成像和三维MRI成像有一些区别。在多层成像中,采集的一层由是一个的二维的切片,只有一个方向被相位编码,每一个切片都用一个二维DFT进行重建。可以按顺序、或者以交错的方式来同时使用SMS技术获取多个切片。而在三维成像中激发厚厚的组织。使用二维空间编码梯度在两个方向进行空间编码,用三维DFT来重建图像。
(1) 三维的SENSE和GRAPPA重建方法
2D SENSE[14]使用线圈敏感度信息在三维体积中展开混叠的像素(它被称为2D SENSE,因为两个相位编码方向都可以被欠采样);三维的GRAPPA被称为2D GRAPPA[15],它使用了一个三维的GRAPPA核,单个线圈中的一个目标点由周围三维邻域中所有线圈的源点的加权和组成,校准数据是作为一个靠近K空间中心的相邻的三维块获得的;SPIRiT和其他相关的并行成像方法也已经推广到三维成像中了。
(2) 2D CAIPIRINHA重建方法
在三维扫描中,沿两个相位编码方向分别进行欠采样可以实现高加速度因子,可以充分利用整个体积内线圈灵敏度的差异。2D CAIPIRINHA(2006年)[16]通过将k空间从标准矩形网格转移到剪切网格上,这种位移改变了混叠模式,使得并行成像重建算法更稳定。2D CAIPIRINHA是三维MRI的MS-CAIPIRINHA的扩展。
(3) WAVE-CAIPIRINHA重建方法
大多数三维并行成像技术只利用线圈两个相位编码方向的线圈灵敏度变化,忽略了读出方向的线圈灵敏度变化。而WAVE-CAIPIRINHA(2015年)[17]可以充分利用三个方向线圈灵敏度的差异。数据用二维CAIPIRINHA采样模式获取,使partitions方向的伪影信号彼此进行位移。此外,在信号读出过程中,还应用了沿y和z的正弦梯度,轨迹呈螺旋桨状。由于应用了CAIPIRINHA采样,以及多个螺旋桨状的轨迹在三维K空间中交错,可以在三个方向分散混叠伪影。
在本节中总结了并行成像的一些经典方法和最新进展,并行成像是一种使用多个接收器线圈来加速MRI磁共振扫描的重建方法。在本节中详细介绍了三种在临床上使用最广泛的重建算法SENSE,GRAPPA和SPIRiT。这些技术可以扩展到3D的MRI成像。此外,在同时在多切片成像中可以利用线圈灵敏度信息来分散伪影。
3.3.压缩感知重建方法
3.3.1 压缩感知原理
在经典信号处理领域,奈奎斯特采样定理一直占据主导地位。奈奎斯特采样定理指出,要把原始信号从采样信号中完整地重构出来,采样频率必须高于信号中最高频率的两倍。这意味着准确地恢复原始信号需要大量的样本数据,这对信号的前端采集系统和后端处理系统都是一个巨大的挑战。因此,在奈奎斯特定理的框架下,如何设计一个同时保证时空分辨率的硬件系统和处理算法一直是信号处理学科的难题。因此,人们首先想到的是数据压缩,因为自然图像和信号在一些变换域具有稀疏性。根据图像的稀疏性,我们采集的信息是冗余的。因此,如何提取信号的有用成分,忽略采集过程中的冗余信息,是近年来信息处理领域的研究热点。
压缩感知(CS)是LUSTIG等人[18]在信息理论和近似理论的文献中的一般背景下提出的。该理论克服了奈奎斯特定理的限制,它在信息论、图像处理、地球科学、光学、微波成像、模式识别、无线通信、等领域受到高度关注。压缩感知理论表明,如果信号在某一个正交空间具有稀疏性(即可压缩性),那么可以设计一个与稀疏变换不相关的测量矩阵,将完备数据投影到测量矩阵上得到欠采样数据,然后通过合适的重建模型和重建算法从非完备的数据集中以高概率精确的重建该信号。一般情况下,MRI图像在一定的变换域(如空间有限差分、小波变换域等)具有稀疏表示,满足压缩感知图像重构的稀疏性要求。而且,利用压缩感知理论可以大大减少傅里叶变换域中的采样数据,从而减少扫描时间,降低对硬件的要求,减少扫描过程中患者的不适。因此压缩感知一经提出,便用来做MRI重建。
3.3.2 压缩感知重建过程
压缩感知算法(Compressed Sensing,CS)方法以远低于奈奎斯特采样定律的采样频率对K空间进行随机欠采样,利用MRI图像在变换域中的稀疏性,通过非线性重建算法消除图像中的非相干伪影,恢复欠采样的K空间数据得到重建图像。图4是压缩感知重建算法的过程。

图4 压缩感知重建算法的过程
在图4中,![]() 是稀疏变换,
是稀疏变换,![]() 是稀疏变换的逆过程,稀疏变换是将图像数据向量映射到稀疏向量的运算符;F代表全采样k空间数据的傅里叶变换,F是全采样k空间数据的傅里叶变换的逆过程,傅里叶变换是将重建图像数据向量映射到k空间向量的运算符。Fu代表欠采样k空间数据的傅里叶变换,Fu是其逆过程。并行成像和 CS 技术都能通过减少K空间采集数据加速成像速度,目前已有一些将两种方法相结合以进一步实现更快的扫描时间的方法。这些方法在重建过程中采用分步重建的方式进行重建,先进行CS重建再进行并行重建或者先进行并行重建再进行 CS 重建,如 CS-SENSE[19]、CS-GRAPPA[20]等。
是稀疏变换的逆过程,稀疏变换是将图像数据向量映射到稀疏向量的运算符;F代表全采样k空间数据的傅里叶变换,F是全采样k空间数据的傅里叶变换的逆过程,傅里叶变换是将重建图像数据向量映射到k空间向量的运算符。Fu代表欠采样k空间数据的傅里叶变换,Fu是其逆过程。并行成像和 CS 技术都能通过减少K空间采集数据加速成像速度,目前已有一些将两种方法相结合以进一步实现更快的扫描时间的方法。这些方法在重建过程中采用分步重建的方式进行重建,先进行CS重建再进行并行重建或者先进行并行重建再进行 CS 重建,如 CS-SENSE[19]、CS-GRAPPA[20]等。
3.4.基于深度学习的MRI重建方法
在3.1到3.3节中,已经介绍了传统的基于部分傅里叶MRI重建方法、并行重建方法和压缩感知重建方法。部分傅里叶MRI重建方法,重建质量一般,一般不用于临床使用。并行成像利用了接收线圈之间的冗余,是临床上最常用的方法。压缩感知是利用基于线性稀疏变换的图像的可压缩性,进行规则化重建的另一种方法。但是在很高的加速度下,并行成像会遭受噪声放大的影响,而压缩感知重建可能会导致残留伪影。而且,压缩感知重建计算复杂,并且需要对正则化参数进行经验上的微调,调参困难,重建速度过慢。
而深度学习是是20世纪80 年代以来人工智能领域研究热点之一。它可以模拟人脑,自动从大量的数据中学习特征表达,实现高度的非线性映射,主要应用于数据建模、预测估计、生物医学等领域,并成功解决了现代计算机无法解决的许多问题。表现出良好的信息并行处理能力、自学能力和推理能力[21]。
Wang等人(2016)[22]首次提出将深度学习引入到快速核磁共振重建方法中,引发了业内学者的关注,从此基于深度学习的MRI重建发展迅速,涌现了一批优秀基于深度学习的MRI重建方法。
从此深度学习引起了人们对高质量加速MRI的兴趣,基于深度学习的重建方法避免的手动调参的困难,并且在临床使用中可以大量缩短扫描时间和重建时间,具有较高的临床使用价值。目前,基于深度学习的MRI重建算法可以大致分为两类,基于数据驱动的端到端的深度学习重建方法和和基于核磁物理成像原理的深度学习重建方法。
3.4.1 基于数据驱动的深度学习重建方法
在基于数据驱动的端到端的深度学习重建方法中,学习了欠采样k空间到完整k空间或者图像的映射,或者学习有伪影的图像到无伪像的映射。这类深度学习方法一般需要大量的高质量的MRI数据来当训练样本和参考图像,来提取MRI数据中的特征进行参数调整和学习。目前常用于MRI重建的网络结构有卷积神经网络(CNN)(2016)[22],U-net网络(2018)[23],Deep Residual(Resent)网络(2018)[24],生成对抗网络( Generative Adversarial Neural Networks,GAN)(2019)[25],深度级联卷积神经网络(Cascade net)[26]等。在此基础上,各种改进的网络不断出现[27-29]。由于篇幅有限,本文主要介绍两种经典的基于数据驱动的深度学习的重建方法。
(1)基于卷积神经网络的重建方法
Wang等人(2016)[22]该方法提出了一种离线卷积神经网络来学习零填充图像到全采样MRI图像之间的端到端映射。图5是基于卷积神经网络的重建方法的过程,离线训练过程中,输入全采样K空间数据,零填充(Zero-filled Images)MR图像为全采样的K数据的直接逆变换,逆变换的结果是含有伪影的质量较差的MRI图像,Ground truth是重建出来的无伪影的MRI图像,其中C表示端到端映射函数。网络训练完成后,学习了一个卷积神经网络。在在线成像阶段,输入欠采样的傅立叶数据到训练好的网络模型中,恢复出准确的高质量的MRI重建图像。

图5 基于卷积神经网络的重建方法的过程
结果表明,该方法的简单重建模型生成的图像非常接近原始图像,没有明显的细节和结构丢失。它表明所提出的网络能够恢复在零填充MR图像中丢弃的细节和精细结构。该网络的训练大约需要三天,但在相同的GPU配置下,每个在线MRI重建所花费的时间不到1秒。而且该网络不仅能够恢复MRI图像的细节和精细结构,而且能够与任何在线重建算法兼容,提高成像的效率。该网络还可以与在线CS-MRI方法结合使用,以实现更高效的成像。
(2)基于深度级联卷积神经网络的重建方法
Schlemper等人(2018)受深度学习最新进展的启发,提出了一个深度学习重建框架,该框架使用卷积神经网络(CNN)的深层级联从欠采样数据中重建二维心脏磁共振(MR)图像的动态序列,以加快数据采集过程,如图6所示。

图6 基于深度级联卷积神经网络的重建方法流程图
结果表明,当每个2D图像帧独立重建时,在重建误差和重建方面,所提出的方法均优于最新的2D压缩感知方法和基于字典学习的MR图像重建。并且算法结合卷积和不同图像帧之间进行参数共享方法,充分利用了动态图像序列中的空间相关性。而且重建速度非常快,每个完整的动态序列都可以在不到10 s的时间内重建,对于2D情况,每个图像帧都可以在23 ms内重建,从而实现了实时应用。
3.4.1 基于物理原理的深度学习重建方法
在基于物理原理的深度学习重建方法中,将传统的重建方法与深度学习相结合,需要考虑到线圈灵敏度和欠采样模式的前向编码算子的知识通过对优化算法进行网络化,从而学习重建模型的最优参数,而不是单纯只学习K空间到图像域或者图像域之间的映射,从而可以增加模型的泛化能力,减少训练数据量。这类方法越来越受到重视,其中典型的方法包括变分网络(2018)(Variational network,VN)[30],基于模型的深度学习(Model-Based Deep Learning)[31],交替方向乘子法(Deep ADMM-Net)[32],近似梯度下降方法(Neural proximal gradient descent)[33],以及一些其他的方法[34-36]。
本文列举两个有代表性的基于物理原理的深度学习重建方法。
(1)基于变分网络的重建方法
Hammernik等人(2018)提出了变分网络(Variational network,VN),该网络先学习该重建过程的逆变换的关键参数,而不是针对每个新数据集解决一个逆问题来为每个新数据集计算一个合适的原始数据和图像之间的变换,以便将模型应用于所有数据集,从而获得加速且高质量的MR图像重建。
在变分网络(VN)方法中,使用测得的原始数据作为输入。线圈灵敏度图是从完全采样的k空间中心预先计算得到的。通过应用伴随算符A*,可从欠采样的k空间数据中计算出零填充解。测得的原始数据和灵敏度图,以及零填充初始化信息被馈送到VN中。灵敏度图用于运算符A和A *中,该运算符执行灵敏度加权的图像组合,还可以执行其他处理步骤,例如消除过采样。而在VN的每次迭代中都需要原始数据和运算符A和A *数据项的梯度,正则化的梯度仅应用于图像域。
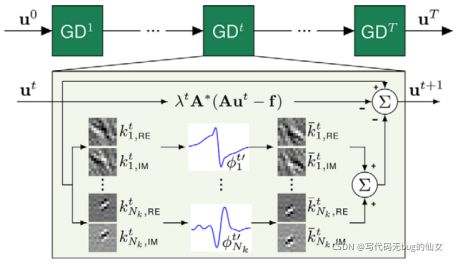
图7 VN网络结构图(Hammernik等人(2018))
在图7的VN方法中,VN由T梯度下降步骤组成。为了获得重构图像,将欠采样的k空间数据,线圈灵敏度图和零填充解输入到VN。在处理复数图像时,我们为实平面和复平面学习了单独的滤波器核Kit,以及学习了非线性激活函数Φit’和数据项权重λt。
训练后,参数θ是固定的,可以通过VN网络前向传播k空间数据来有效地重建测试集的k空间数据。训练过程如图8所示。
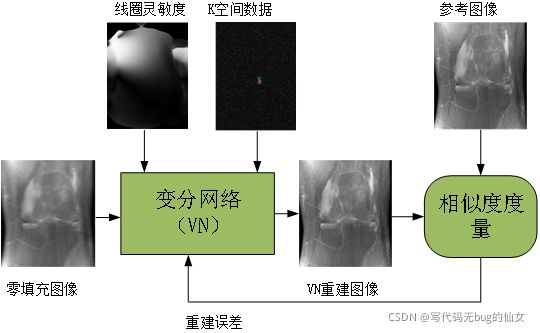
图8 VN网络训练过程图(Hammernik等人(2018))
收集到的磁共振扫描数据即全采样k空间数据作为输入,线圈灵敏度图是从完全采样的k空间中心预先计算得到的,测得的原始数据和灵敏度图,被馈送到变分网络中。训练数据和测试数据都是经过相同的欠采样方法进行处理,得到欠采样数据和线圈灵敏度图。训练数据在经过变分网络训练完成之后,从而学习到重建过程的逆变换的关键参数,即训练好了所需要的参数模型,最后将该模型应用到线上重建部分对测试数据进行重建测试。
(2)基于物理方法的自监督重建网络
Yaman等人(2018)提出了一种基于数据的欠采样自监督学习的网络(SSDU),用于基于物理学的深度学习(DL)重建。该网络将可用的观测数据分为两组,其中一组用于展开网络中的数据一致性单元,另一组用于定义训练损失,网络结构如图9所示。并使用公开的fastMRI膝关节数据集,与监督学习方法、传统的压缩感知和并行成像方法进行了比较。

图8 基于物理方法的自监督重建过程(Yaman等(2018))
结果表明所提出的自监督方法在没有全采样K空间数据的情况下,能够达到与监督非常接近的学习效果,可以重建出类似于监督学习的MRI图像。而且该方法在定量指标上明显优于传统的压缩感知和并行成像重建方法。
四、总结
本报告主要简要介绍了核磁共振成像原理,然后介绍四大类核磁共振重建方法的发展之路,包括部分傅立叶重建方法、并行成像重建方法、压缩感知重建方法和基于深度学习的重建方法。对于部分傅里叶重建方法,本报告主要介绍了零填充、共轭对称、Homodyne等多个方法;对于并行成像方法,本报告主要介绍了SENSE、GRAPPA和SPIRiT等临床实践中最常用的重建技术,以及同时多层重建方法和三维的并行成像技术;对于压缩感知重建方方法,本报告主要介绍了压缩感知重建的原理以及在核磁共振重建中的应用;对于深度学习重建方法,本报告主要介绍了基于数据驱动的端到端的深度学习重建方法和基于核磁物理成像原理的深度学习重建这两大类方法,并介绍了几个经典的深度学习重建方法。基于数据驱动的端到端的深度学习重建方法中主要介绍了基于卷积神经网络CNN和深度级联网络的重建方法,基于核磁物理成像原理的深度学习重建方法主要介绍了基于变分网络和基于物理方法的无监督重建方法。
部分傅立叶重建方法、并行成像重建方法、压缩感知重建方法都属于传统的核磁共振重建方法,这些方法提出的比较早,而并行成像方法已经在临床上使用多年,已经成为临床上最常用的重建方法。但是传统的重建方法也存在着一些问题,例如加速倍数低、算法迭代时间长、复杂度高、参数选择困难等。而深度学习可以自动从大量数据中学习特征表达,实现高度的非线性映射。自从深度学习在核磁共振重建中应用以来,基于深度学习的重建方法发展迅速,涌现了一大批优秀的深度学习重建方法。
随着深度学习在核磁共振重建领域的深入研究和应用,也面临这一些问题。例如,医学图像数据很难获得,一般都是小样本的数据,而深度学习训练需要大量的训练数据。以下几个方法可以用来缓解这一问题,1)基于物理驱动的深度学习重建方法,该方法将传统的重建方法与深度学习相结合,从而学习重建模型的最优参数,而不是单纯只学习K空间到图像域或者图像域之间的映射,从而可以增加模型的泛化能力,减少训练数据量。2)数据增强,在训练之前对数据进行数据增强来扩充数据集,以增加模型的泛化能力和降低模型复杂度。3)迁移学习,迁移已有的深度学习模型到新的重建任务中。此外,医学图像的标注也是一个严重制约深度学习在核磁共振重建中发展的一个重大因素,所以无监督学习的研究和发展显得格外重要。另外,可解释性在核磁共振重建中也十分重要,如何提升深度学习在核磁共振重建中的可解释性是一直以来的难点,需要在这方面继续进行研究。
虽然,近几年深度学习在核磁共振重建方法的研究中一直都是热点研究问题,但临床上使用最广泛的还是传统的并行成像方法。深度学习的重建方法在临床应用方面还有待进一步研究,以实现深度学习重建方法在核磁共振扫描仪产品上的广泛落地应用。
参考文献
1.Jesse Hamilton,Dominique Franson,Nicole Seiberlich. Recent advances in parallel imaging for MRI[J]. Progress in Nuclear Magnetic Resonance Spectroscopy,2017,101.
2.核磁共振成像学.俎栋林-北京:高等教育出版社,2004.1.IBSN 7-04-012966-3
3.何汶静,陈晓文,朱高杰,罗海.磁共振图像处理中部分傅里叶重建算法的比较[J].重庆医学,2016,45(20):2804-2806+2809.
4.Klaas, P, Pruessmann, et al. SENSE: Sensitivity encoding for fast MRI[J]. Magnetic Resonance in Medicine, 1999.
5.Blaimer M,Breuer F,Mueller M,et a1.SMASH,SENSE,PILS,GRAPPA:How to Choose the Optimal Method[J] Topics in Imaging,2004,15(4):223
6.Sodickson D K,Manning W J.Simultaneous Acquisition of Spatial Harmonics(SMASH):Fast Imaging with Radiofrequency Coil Arrays[J].Magnetic Resonance in Medicine,1997,38(4):591—603.
7.akob P M,Griswold M A,Edelman R R,et a1.AUTO-SMASH:A Self—Calibrating Technique for SMASH Imaging [J].Magnetic Resonance Materials in Physics,Biology and Medicine,1998,7(1):42—54.
8.Heidemann R M,Griswold M A,Haase A,et a1.VD-AUTO—SMASH Imaging[J].Magnetic Resonance in Medicine, 2001,45(6):1066—1074.
9.M.A. Griswold, P.M. Jakob, R.M. Heidemann, M. Nittka, V. Jellus, J. Wang, B. Kiefer, A. Haase, Generalized autocalibrating partially parallel acquisitions (GRAPPA), Magnet Reson Med, 47 (2002), 1202-1210. doi:10.1002/mrm.10171
10.M. Lustig, J.M. Pauly, SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space, Magn. Reson. Med. 64 (2010) 457–471.
11.M. Murphy, M. Alley, J. Demmel, K. Keutzer, S. Vasanawala, M. Lustig, Fast l1- SPIRiT compressed sensing parallel imaging MRI: scalable parallel implementation and clinically feasible runtime, IEEE Trans. Med. Imag. 31 (2012) 1250–1262.
12.M. Uecker, P. Lai, M.J. Murphy, P. Virtue, M. Elad, J.M. Pauly, S.S. Vasanawala, M. Lustig, ESPIRiT - an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA, Magn. Reson. Med. 71 (2014) 990–1001.
13.M. Barth, F. Breuer, P.J. Koopmans, D.G. Norris, B.A. Poser, Simultaneous multislice (SMS) imaging techniques, Magn. Reson. Med. 75 (2016) 63–81.
14.M. Weiger, K.P. Pruessmann, P. Boesiger, 2D SENSE for faster 3D MRI, Magn. Reson. Mater. Phys. Biol. Med. 14 (2002) 10–19.
15.M. Blaimer, F.A. Breuer, M. Mueller, N. Seiberlich, D. Ebel, R.M. Heidemann, M. A. Griswold, P.M. Jakob, 2D-GRAPPA-operator for faster 3D parallel MRI, Magn. Reson. Med. 56 (2006) 1359–1364.
16.F.A. Breuer, M. Blaimer, M.F. Mueller, N. Seiberlich, R.M. Heidemann, M.A. Griswold, P.M. Jakob, Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA), Magn. Reson. Med. 55 (2006) 549–556.
17.B. Bilgic, B.A. Gagoski, S.F. Cauley, A.P. Fan, J.R. Polimeni, P.E. Grant, L.L. Wald, K. Setsompop, Wave-CAIPI for highly accelerated 3D imaging, Magn. Reson. Med. 73 (2015) 2152–2162.
18.LUSTIG M, DONOHO D, PAULY JM. Sparse MRI: The application of compressed sensing for rapid MR imaging.[J]. Magnetic resonance in medicine: official journal of the Society of Magnetic Resonance in Medicine,2007,6(6).
19.LIANG D, LIU B, WANG J, et al. Accelerating SENSE using compressed sensing[J]. Magn Reson Med, 2009, 62(6): 1574-1584.
20.HUANG Li-jie, SONG Yang, ZHAO Xian-ce, XIE Hai-bin, WU Dong-mei, YANG Guang. A New Combination Scheme of GRAPPA and Compressed Sensing for Accelerated Magnetic Resonance Imaging[J]. Chinese Journal of Magnetic Resonance, 2018, 35(1): 31-39.
21.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature 2015 may;521(7553):436–444. http://dx.doi.org/10.1038/ nature14539.
22. Wang S , Su Z , Ying L , et al. Accelerating magnetic resonance imaging via deep learning[C]// 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI 2016). IEEE, 2016.
23.Jure Zbontar, Florian Knoll, Anuroop Sriram, et al. fastMRI: An Open Dataset and Benchmarks for Accelerated MRI.[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2018, abs/1811.08839
24.Lee D, Yoo J, Tak S, Ye JC. Deep Residual Learning for Accelerated MRI Using Magnitude and Phase Networks. IEEE Trans Biomed Eng 2018;65(9):1985-1995.
25.Mardani M, Gong E, Cheng JY, Vasanawala SS, Zaharchuk G, Xing L, Pauly JM. Deep Generative Adversarial Neural Networks for Compressive Sensing MRI. IEEE Trans Med Imaging 2019;38(1):167-179.
26.Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2018;37(2):491-503.
27.Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain transform manifold learning. Nature 2018;555(7697):487-492.
28.Liang D, Cheng J, Ke Z, Ying L. Deep MRI Reconstruction: Unrolled Optimization Algorithms Meet Neural Networks. arXiv preprint arXiv:1907.11711; 2019.
29.Akcakaya M, Moeller S, Weingartner S, Ugurbil K. Scan-specific robust artificial-neuralnetworks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging. Magn Reson Med 2019;81(1):439-453.
30.Hammernik et al., Learning a variational network for reconstruction of accelerated MRI data, Magnetic Resonance in Medicine, 79(6), pp. 3055-3071, 2018.
31.Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans Med Imaging 2019;38(2):394-405.
32.Yang Y, Sun J, Li H, Xu Z. Deep ADMM-Net for compressive sensing MRI. Advances in neural information processing systems; 2016. p 10-18.
33.Mardani M, Sun Q, Donoho D, Papyan V, Monajemi H, Vasanawala S, Pauly J. Neural proximal gradient descent for compressive imaging. Advances in Neural Information Processing Systems; 2018. p 9573-9583.
34.Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2019;38(1):280-290.
35.Gregor K, LeCun Y. Learning fast approximations of sparse coding. International Conference on International Conference on Machine Learning; 2010. p 399-406.
36.Yaman B , Hosseini S , Moeller S , et al. Self-Supervised Learning of Physics-Based Reconstruction Neural Networks without Fully-Sampled Reference Data[J]. Magnetic Resonance in Medicine.