统计学习方法——概述

统计学习方法之概述

---

1.统计学习的特点

(1)统计学习以计算机及网络为平台，是建立在计算机及网络上的;

(2) 统计学习以数据为研究对象，是数据驱动的学科

(3) 统计学习的目的是对数据进行预测与分析;

(4) 统计学习以方法为中心，统计学习方法构建模型井应用模型进行预测与分析;

(5) 统计学习是概率论、统计学、信息论、计算理论、最优化理论及计算机科学等多个领域的交叉学科，并且在发展中逐步形成独自的理论体系与方法论

2.统计学习的步骤

(1)得到一个有限的训练、数据集合；

这一步的目的就是获取数据集，很多时候的数据集其实是我们通过爬虫的技术自己进行爬取得到的，但也有一些通用的数据集，比如说图像识别里面的voc数据集还有coco数据集等等的一些。

(2)) 确定包含所有可能的模型的假设空间，即学习模型的集合;

通俗点讲就是检索所有相关的的模型

(3) 确定模型选择的准则，即学习的策略;

找出最合适你想使用的一种算法的模型，其目的是提高准确率等一些参数

(4) 实现求解最优模型的算法，即学习的算法；

学习预测，通俗讲就是让你的模型通过你的数据集进行学习

(5) 通过学习方法选择最优模型；

通过对学习的效率的对比，选择出最合理的模型，以及调好相关的参数

(6)利用学习的最优模型对新数据进行预测或分析。

把学习好的模型进行应用的实战，实现最后的预测工作，其实在上面的步骤里还可以加入验证集，其目的就是检验你算法模型学习能力的强弱，来对它进行的考核考验

3.监督学习

（1）监督学习

监督学习是指从标注数据中学习预测模型的机器学习问题。通俗一点讲就是你的数据集里包含了部分输出的预测结果，然后你给新的条件让它在进行一些预测工作，比如说就是红色的，硬的，香的苹果我给定它可以被当作是一个好苹果，这里面的红色的，硬的，香的就可以作为数据的特征，不同的特征叫做不同的维度，被当作好苹果就可以当作是一个标签，也可以当作是已知的预测结果，比如说再让你预测一个别的特征的苹果是否是好苹果，这就是一个典型的监督学习的例子，它与无监督最大的区别就是是否包含标签。
再解释几个专业的名词：输入空间，输出空间，特征空间，其实简单理解就是将输入与输出所有可能取值的集合分别称为输入空间与输出空间，他在形式上其实多样性的，包含任意的属性东西，可以是有限的集合也可以是整个欧式集合。特征空间就是特征向量组成的集合，以及对于维度的定义在前面几句话里都解释清楚了，不做过多的阐述。
在监督学习中，输入输出变量用大写字母表示，习惯上输入变量写作X输出变量写为Y。输入输出变量的取值用小写字母x表示，输入变量的取值用小写字母y表示，变量可以是标量或向量，都用相同类型字母表示。

(2) 联合概率分布

联合概率P(X ，Y)，不做过多的解释，可以理解为函数关系，可以把输入理解为x，输出理解为y。

(3) 条件概率

也很好理解，P(X|Y)，简单来讲就是在y的条件下x发生的概率，他和联合分布还是有区别的，注意理解。

3.统计学习三要素

(1)模 型(假 设 空 间 ）

在监督学习过程中，模型就是所要学习的条件概率分布或决策函数。模型的假设空间 (hypothesis space) 包含所有可能的条件概率分布或决策函数。例如，假设决策函数是输入变量的线性函数，那么模型的假设空间就是所有这些线性函数构成的函数集合。假设空间中的模型一般有无穷多个。
决策函数构成的函数集合形成的假设空间表示为：

条件概率构成的函数假设空间

(2) 策略

有了模型的假设空间，统计学习接着需要考虑的是按照什么样的准则学习或选择最优的模型 统计学习的目标在于从假设空间中选取最优模型。
首先引入损失函数与风险函数的概念。损失函数度量模型预测一次的好坏，风险函数度量平均意义下模型预测的好坏。
损失函数其实就是说告诉你预测错了，然后通过不同的计算方法计算出你和正确结果之间的偏差是多少。损失值越少模型就越好。

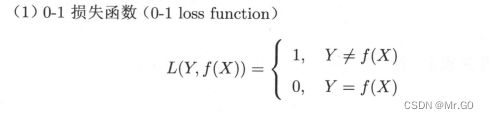
0-1损失函数就是告诉你对的就是对的，你只能知道你的是否是正确或者错误，但是无法评判你和正确之间的差距是多少，后面的几个算法就是通过平方，绝对值等计算出你们之间的差距是多少。



经验风险又称为或经验损，它是关于训练数据集的平均损失，换句话说就是知道了上面的单个计算损失的方法，要计算整个数据集的损失所使用中的一种求和平均的方法吧，记作如下：

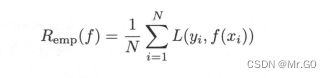
期望损失
这是理论上模型 f(X) 关于联合分布 P(X， Y) 的平均意义下的损失，称为风险函或期望损失 ，记作如下：

期望风险是模型关于联合分布的期望损失，经验风险是模型关于训练样本集的平均损失。
由于现实中训练样本数目有限，甚至很小，所以用经验风险估计期望风险常常并不理想，要对经验风险进行一定的矫正。这就关系到监督学习的两个基本策略，经验风险最小化和结构风险最小化。
经验风险最小化：就是说把训练集中的每一个样本都给跑一遍，每一个样本都进行计算

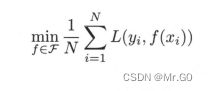
结构风险最小化：就是加了一个正则项，也就是一个复杂度，模型越复杂，那一项就越大。为了防止模型的训练过度拟合

(3) 算法

算法是指学习模型的具体计算方法。统计学习基于训练数据集，根据学习策略，从假设空间中选择最优模型，最后需要考虑用什么样的计算方法求解最优模型。这时，统计学习问题归结为最优化问题，统计学习的算法成为求解最优化问题的算法。如果最优化问题有显式的解析解，这个最优化问题就比较简单。但通常解析解不存在，这就需要用数值计算的方法求解。如何保证找到全局最优解，并使求解的过程非常高效，就成为一个重要问题。统计学习可以利用己有的最优化算法，有时也需要开发独自的最优化算法。

4.模型评估与模型选择

样本训练完毕，你怎么能确定哪个模型是比较好的，就引入了训练误差和测试误差的概念

(1)训练误差和测试误差

简单来说就是在测试样本的时候我拿训练集里的东西拿来测试，看你学了多少东西，举个例子就是说，学校的期末考试，期末考的东西就是原封不动的学习了的东西，你的考试成绩就是训练误差的结果。
同理，测试误差就是单独划分一个作为测试集来考核模型的学习能力，类比与学校的期末考试全部换全新的相关考题，不会和你学习了的一模一样来检验你的学习结果。公式如下图

在引入一个概念叫做验证集，所谓验证集就是为了解决在测试集测试的时候恰恰测试的那几个样本就是该模型学习后最擅长或者最不擅长的造成结果的偏大或者偏低，举个例子来说就是期末考试出的新题恰好就是你最拿手的或者最不拿手的，很显然这根本不可能反映出你的真实水平，那么为了防止这种情况的发生，就引入了验证集，在验证集里结果最好的模型再拿来做测试误差。

(2) 拟合问题

如果一味追求提高对训练数据的预测能力，所选模型的复杂度则往往会比真模型更高。这种现象称为过拟合 过拟合是指学习时选择的模型所包含的参数过多，以至出现这模型对己知数据预测得很好，但对未知数据预测得很差的现象。
简单理解就是说为了干某件事而让他刻意学习这件事，那么这个模型对于除了学习的相关特征的预测能力有很强的把控，对于其它的肯定会逊色的多，这就是典型的过拟合问题。
判断过拟合最直接的方式就是看它在未知的测试集里预测能力的把控和已知的训练集预测把控的差距，如果差距较为明显很显然就是存在过拟合的状态，因为好的学习肯定不仅仅包含学习训练集的数据，还要对测试集的数据有良好的处理能力。

5.正则化与交叉验证

（1）正则化

减少模型的过复杂的问题，前面有具体的讲述的，在这不做过多的赘述。

（2）交叉验证

数据集被划分为三类分别是：
训练集：用来训练模型，就是说为了让模型进行学习而引入的数据，理解为自学习的东西那部分数据；
测试集：用与模型的选择，就是说通过测试集的数据结果来选择一个适合当前使用的一个模型进行预测学习；
验证集：是为了检验模型和预测能力和学习能力，是对模型最直接的评估的一组数据。
在学习到的不同复杂度的模型中，选择对验证集有最小预测误差的模型。但是，在许多实际应用中数据是不充足的。为了选择好的模型，可以采用交叉验证方法。交叉验证的基本想法是重复地使用数据，把给定的数据进行切分，将切分的数据集组合为训练集与测试集，在此基础上反复地进行训练、测试以及模型选择。
简单交叉验证：首先随机地将己给数据分为两部分， 一部分作为训练集，另一部分作为测试集，然后用训练集在各种条件下(例如，不同的参数个数)训练模型，从而得到不同的模型，在测试集上评价各个模型的测试误差，选出测试误差最小的模型。
S交叉验证：:首先随机地将已给数据切分为 互不相交、大小相同的子集 ，然后利用 S-1个子集的数据训练模型，利用余下的子集测试模型 ，将这过程对可能的S 种选择重复进行;最后选出次评测中平均测试误差最小的模型。其实还是很好理解的，就是划分子集，选择一个作为训练模型，把剩下的拿来一遍遍的测试，然后选择出最好的模型。
留一交叉验证：不写概念定义了，直白点讲就是把上面S里的子集划分化为每个里面只有一个数据的情况进行处理，很显然这种情况就是对于数据过少的情况而定的。

6.泛化能力

(1)泛化误差

所谓的泛化能力指的就是模型对结果的预测能力，很常见的就是引入了测试集来评判这种能力，很显然是存在弊端的，因为测试集是有限的，得到的结果也不一定就是准确的，具体带来的误差可以参照我前面提到过的，所以说就是引入了泛化误差试图从理论上对预测能力的分析，实际上泛化误差其实就是前面提到的期望风险。前面也是有提到的，这里就不多解释了。

(2)泛化误差上界

就是字面意思，直接说明该模型的预测能力上限是多少，看你是否可以接受，就是这样的 一个意思。

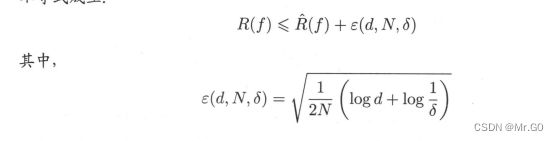
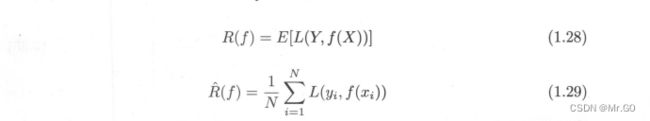
先讲1.28这个公式，公式里的L其实就是loss函数的缩写，简单理解就是，假如说你有二十个数据对它进行预测，把预测结果和真实结果都一样的记作0（也就是所谓的预测正确），把预测的和真实的不一样的记作1，每一个数据都有一个0或者1与之对应，这样所形成的一个loss函数，就是1.28。然后把每一组形成的0或者1相加起来在除以总样本数就形成了1.29这个公式。其实这两个公式的理解还是很好理解的。
所以说回到上图的不等式，就说明我的泛化误差其实是小于期望误差加上一个数的，这就是泛化误差的上界。实际的应用中你可以计算后面的数据的大小来确定你是否可以接受这个模型带来的误差。这个证明应用不常见，就不讲解了。
泛化误差的缺点很显然就是规定的有限个集合，就因为这个有限个的限限制导致这个公式使用是很不好用的。

3.生存模型与判别模型

(1)生成方法

具体讲就是先算出联合概率在计算出x的概率，然后在计算出条件概率，举个例子就是你要想知道某一个人的名字，你可以通过了解他的父母亲来直接得知他的名字。典型的生成模型有朴素贝叶斯法和隐马尔可夫模型。

(2)判别方法

判别方法由数据直接学习决策函数 f(X) 或者条件概率分布 P(YIX) 作为预测得出的，举个例子就是计算出他叫张三的概率是多少，计算出他叫李四的概率是多大，然后再通过概率确定谁是谁。 判别方法关心的是对给定的输入应该预测什么样的输出，典型的判别模型包括 :k 近邻法、感知机、决策树、逻辑斯谛回归模型、最大烟模型、支持向量机、提升方法和条件随机场等。

7.监督学习的应用

(1)分类问题

在学习过程中，根据己知的训练数据集利用有效的学习方法学习 个分类，在分类过程中，利用学习的分类器对新的输入实例进行分类。

精确率
召回率

Fl 值是精确率和召回率的调和均值

(2)标注问题

标注问题的输入是个观测序列，输出是个标记序列或状态序列。标注问题的目标在于学
习一个模型，使它能够对观测序列给出标记序列作为预测。比如说通过输入进去的几句话，来确定输入的语气等等，比如，“妹妹乖，不哭，哥哥抱抱”通过标志里面的乖，不哭，抱抱等就可以预测出实际的场景情况等。

(3)回归问题

回归用于预测输入变量(自变量)和输出变量(因变量)之间的关系，特别是当输入变量的值发生变化时，输出变量的值随之发生的变化。理解为一种函数一一对应的一种关系。