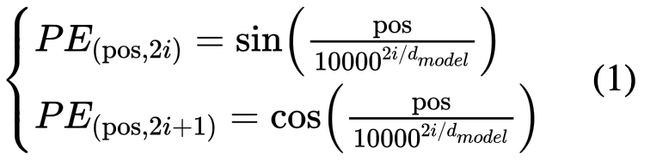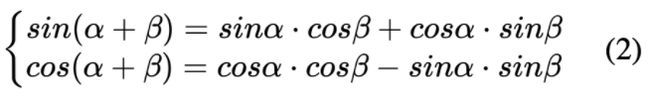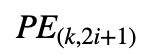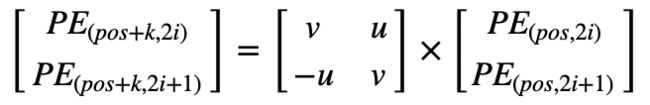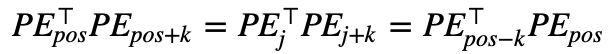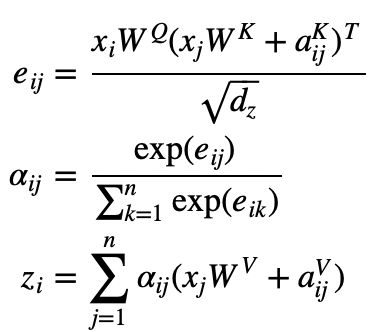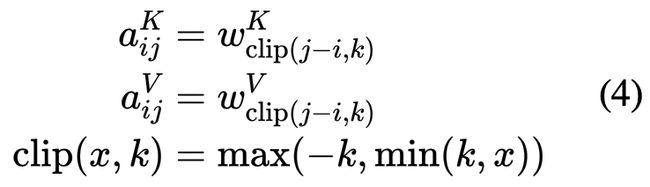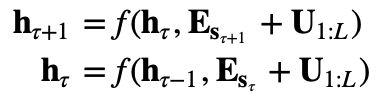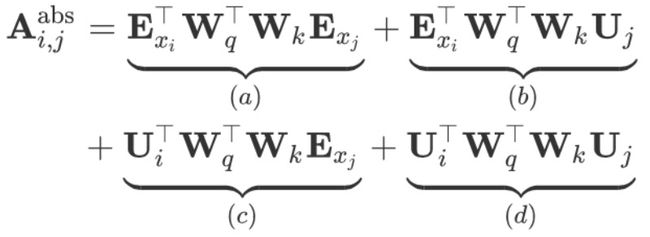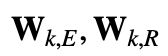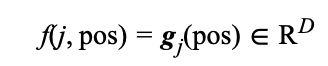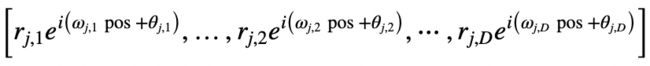【工大SCIR笔记】浅谈Transformer模型中的位置表示
作者:哈工大SCIR 徐啸
0. 何为位置信息
首先简单谈一下位置信息。一般将位置信息简单分为绝对位置信息和相对位置信息,并且前者对句子语义的影响不大,更为重要的是后者。
以情感分析 (Sentiment Analysis) 为例:
I like that you don’t have a lot of money.
[Positive]I don’t like you because you have a lot of money.
[Negative]
don’t 与 like 的相对位置不同(包括相对距离不同和方向不同),决定了这两句话的情感取向是一正一负的,可见单词的相对位置对语义有关键性影响。不过,在传统词袋(Bag-Of-Words, BOW)模型中,这两句话得到的句子表征却是一致的。
再以命名实体识别 (Named Entity Recognition, NER) 为例[4]:
图1 命名实体识别示例
一般而言,在 Inc. 之前的单词为ORG ,而在 in 之后为 TIME 或 LOC 。但是同为 Louis Vuitton ,与 Inc. 相距较远的为PER,指的是创立者这一实体,而相距较近的为ORG,指的是组织(公司)这一实体。可见,单词之间的相对位置在 NER 任务中是十分重要(敏感)的。
需要注意的是,相对位置是具有方向性的,即 Inc. 与 in 的相对距离为 -1,1854 与 in 的相对距离为 1
那么,如何对位置信息进行表示呢?
下文结合 Transformer 的位置表示、RPR、Transformer-XL 以及 Complex Embeddings,试解释位置信息的表示问题。
1. Transformer 的位置表示
原始 Transformer[1] 中使用 Positional Encoding 生成固定的位置表示。
其中,pos 指的是 token 的位置。设句子长度为L,那么![]() 。i 是
。i 是![]() 维词向量的某一维,例如
维词向量的某一维,例如![]() 时,
时,![]() 。因此,借助上述正余弦公式,我们可以为每个位置生成
。因此,借助上述正余弦公式,我们可以为每个位置生成![]() 维的位置向量。
维的位置向量。
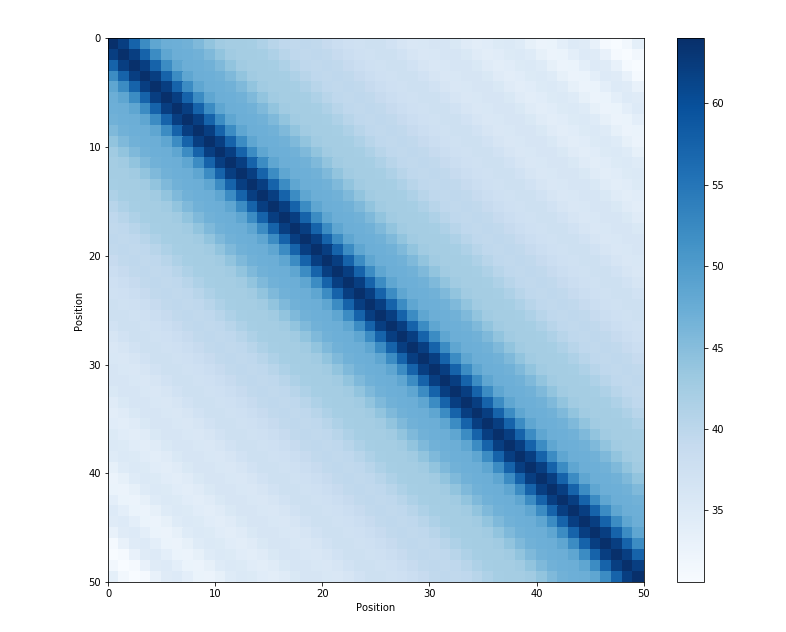
图2以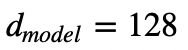 为例,横坐标为位置表示的维数
为例,横坐标为位置表示的维数![]() ,纵坐标为位置 pos 。不难发现,当维数逐渐从 0 变为 127,周期相应的从 2π 变为 2π*10000,不同位置之间的差异性变得越来越模糊。
,纵坐标为位置 pos 。不难发现,当维数逐渐从 0 变为 127,周期相应的从 2π 变为 2π*10000,不同位置之间的差异性变得越来越模糊。
图2 正弦位置编码可视化[10]
为什么会选择如上公式呢?作者表示:
We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k,
can be represented as a linear function of
已知三角函数公式如下:
结合公式 (1) (2) 可得
u, v 可得下式:
因此,可以将 可以表示为
可以表示为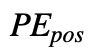 的线性表示。作者希望借助上述绝对位置的编码公式,让模型能够学习到相对位置信息。
的线性表示。作者希望借助上述绝对位置的编码公式,让模型能够学习到相对位置信息。
接着我们来看,两个不同位置的位置嵌入之间的点积。推导可得,其点积虽然能够反映相对距离,但它缺乏方向性,并且这种特性(相对距离)会被原始 Transformer 的注意力机制破坏[4]:
基于公式(1) ,pos 位置的位置嵌入可以表示为:
其中,d 表示位置嵌入的维度,![]() 表示由 i 决定的常量
表示由 i 决定的常量 ,由
,由![]() 可推得:
可推得:
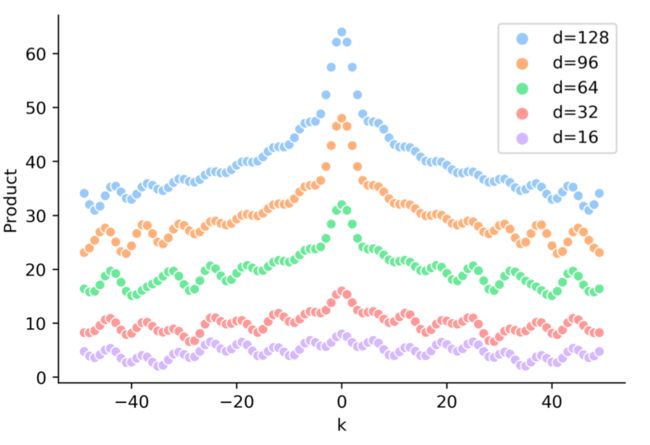
因此,对于给定的位置 pos 和 偏移量 k 而言, 只取决于偏移量 k,内积会随着相对位置的递增而减小。因此两者的点积可以反映相对距离 k。如图3所示,点积的结果是对称的,并且随 |k| 增加而减少(但并不单调)。
只取决于偏移量 k,内积会随着相对位置的递增而减小。因此两者的点积可以反映相对距离 k。如图3所示,点积的结果是对称的,并且随 |k| 增加而减少(但并不单调)。
图3 TENER[4] 中对点积结果的可视化
此外,由于点积结果只依赖于 k,那么令![]() ,可以由公式 (3) 可得:
,可以由公式 (3) 可得:
那么,对于给定的位置 pos 和偏移量 k 而言:
也即两者的点积无法反映方向性。
如图4所示,两者点积的结果是对称的,并且随着位置的增大而减小。
图4 Sinusoidal position encoding 点积可视化[10]
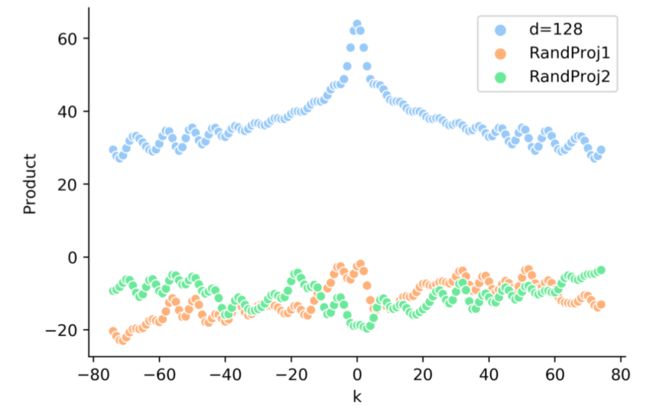
但是在 Transformer 中,由于需要经过映射,即两者间的点积实际是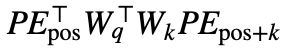 并可以视为
并可以视为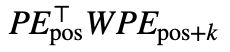 ,然而如图5所示,此时并没有看到相对距离 k 的清晰模式。
,然而如图5所示,此时并没有看到相对距离 k 的清晰模式。
图5 TENER[4] 中对包括映射矩阵后的点积结果的可视化
另外,Transformer 之前的 ConvSeq[5] 以及之后的 BERT[6] 都没有选择使用 Positional Encoding 的方式生成位置表示,而是采取了所谓的 learned and fixed 的可学习的 Position embedding。也就是去训练一个位置嵌入矩阵,大小为![]() ,这里暂且按下不表。
,这里暂且按下不表。
2. 相对位置表示
Relative Position Representations[2](下文简称为 RPR) 一文中认为,RNN 通常依靠其循环机制,结合 t 时刻的输入和前一时刻的隐层状态 计算出
计算出![]() ,直接通过其顺序结构沿时间维度捕获相对和绝对位置。而非 RNN 模型不需要顺序处理输入,则需要显式编码才能引入位置信息。
,直接通过其顺序结构沿时间维度捕获相对和绝对位置。而非 RNN 模型不需要顺序处理输入,则需要显式编码才能引入位置信息。
Transformer 中的 Self-attention 机制如下,输入 ,输出
,输出 :
:
RPR 不在输入时将位置表示与 token 表示相加,而是选择对 self-attention 进行改动:
因此,模型学习相对位置表示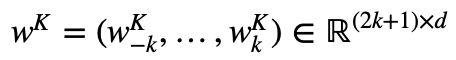 (
( 同理),同一层的attention heads之间共享,但是在不同层之间是不同的。
同理),同一层的attention heads之间共享,但是在不同层之间是不同的。
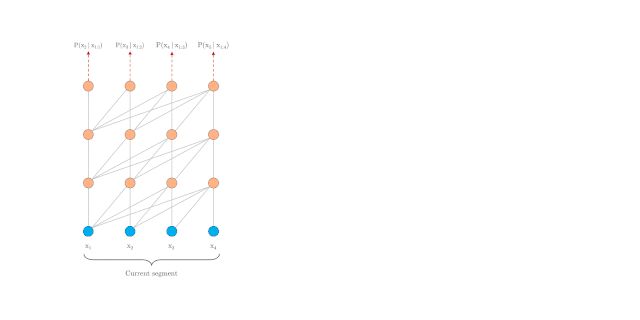
此处公式有些晦涩,故此举一实例[7]加以解释:
当 k=4 时, ,那么WK的每一行则分别对应的是位置 i 与位置
,那么WK的每一行则分别对应的是位置 i 与位置![]() 之间的相对位置表示。以输入“I think therefore I am”为例:
之间的相对位置表示。以输入“I think therefore I am”为例:
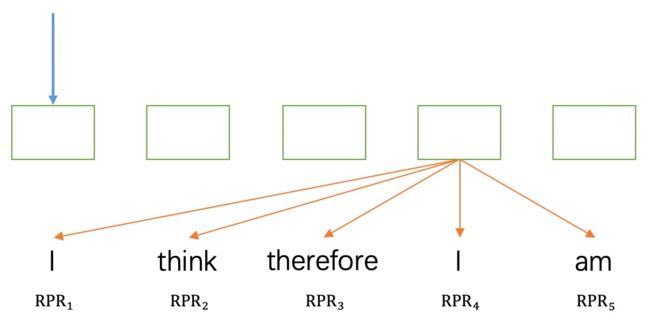
如图6所示,“I” 使用的是![]() ,“think” 使用的是
,“think” 使用的是![]() ,因为 “think” 在第一个 “I” 的右边第一个,对应的是 i+1的情况。也即,Query 为 “I”,Key 为“think”时,有 i=0, j=1 ,由公式 (4) 可知,
,因为 “think” 在第一个 “I” 的右边第一个,对应的是 i+1的情况。也即,Query 为 “I”,Key 为“think”时,有 i=0, j=1 ,由公式 (4) 可知,![]() ,那么此时
,那么此时![]() 。
。
图6 RPR 示例 1
如图7所示,“I” 使用的是![]() ,“think” 使用的是
,“think” 使用的是![]() (因为 “think” 在第二个 “I” 的左边第二个,对应的 i-2 的情况)。
(因为 “think” 在第二个 “I” 的左边第二个,对应的 i-2 的情况)。
图7 RPR 示例 2
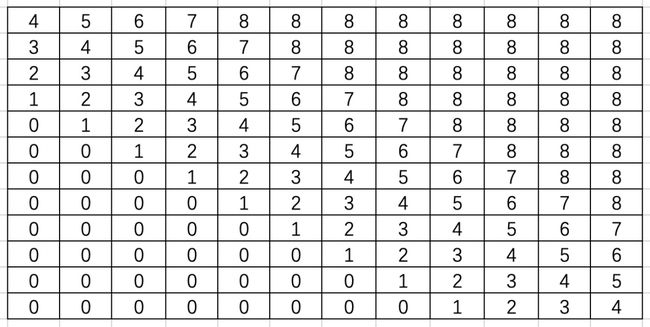
另外,作者认为精确的相对位置信息在超出了一定距离之后是没有必要的,并且截断后会使得模型的泛化效果好,即可以更好的泛化到没有在训练阶段出现过的序列长度上。
这里试举一例帮助理解。当输入句子长度为 12 且 k = 4 时, RPR 的嵌入矩阵如图8所示:
图 8:RPR 嵌入矩阵
不过,论文在对机器翻译任务进行消融实验(表1所示)时发现,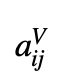 可能并不是必要的。第3节中的 Transformer-XL 也略去了这一项。
可能并不是必要的。第3节中的 Transformer-XL 也略去了这一项。
表1 RPR 消融实验结果
![]()
此外,RPR 一文并未开源代码,这里给出Github 上 TensorFlow (https://github.com/THUNLP-MT/THUMT/blob/d4cb62c215d846093e5357aa17b286506b2df1af/thumt/layers/attention.py)和 PyTorch (https://github.com/MjolnirX/relative-position-pytorch/blob/master/relative_position.py)两个版本的实现。
3. Transformer-XL
Transformer-XL一文并没有采用 RPR 中的相对位置表示方式,而是开创性的在片段循环机制下提出了 Relative Positional Encodings,实现仅在隐藏状态中对相对位置信息进行编码。
尽管 Al-Rfou et al. (2018)[8] 成功地在字符级语言建模中训练了深度(64 层) Transformer 网络,效果超越了 LSTM,但是其输入为分离的、固定长度(几百个字符)的片段,并且没有跨片段的信息传递。由于固定的上下文长度,模型无法捕获超出预定义的上下文长度的任何长期依赖。另外,固定长度的片段是通过选择连续的字符块而创建的,并未考虑句子边界或任何其他语义边界。因此,该模型缺乏必要的上下文信息来较好地预测最初的几个字符,这会导致无效的优化和较差的性能。
作者将此问题称为上下文碎片(context fragmentation)。如果给定无限的存储和计算能力,一个简单的解决方案就是使用无条件的 Transformer 解码器来处理整个上下文序列,类似于前馈神经网络。然而在实践中由于资源有限,通常是不可行的。为了解决这一问题,作者提出了片段循环机制(segment-level recurrence) 和新的相对位置嵌入(Relative Positional Encodings)。
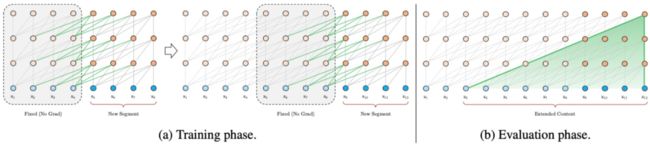
首先深入探究 Al-Rfou 等人的做法,下文将其称为原始模型。如图 9.a 所示, 原始模型将整个语料库拆分为长度受限的片段,并且只在每个片段内训练模型,忽略了来自先前片段的所有上下文信息。这使得训练过程中(图 10),信息不会在 forward 或 backward 过程中跨片段流动,而且这使得最大依赖长度受到了片段长度的限制(这本是 Self-attention 的优势)。其次,虽然可以通过 padding 来考虑句子边界或任何其他语义边界,但是在实践中直接简单分块已成为提高效率的标准做法。这也就是作者说的上下文碎片问题。
图9 原始模型训练与评估流程可视化(片段长度为 4)
 图10 动态演示: vanilla model 的训练过程[9]
图10 动态演示: vanilla model 的训练过程[9]
在评估过程中(图11),原始模型也在每一步中消耗与训练中相同长度片段,但仅在最后一个位置进行预测。然后,在下一步仅将片段向右移动一个位置,并且重新进行计算。如图 9.b 所示,如此可确保每一步预测都能利用训练期间暴露的最长可能上下文,并且还缓解了训练中遇到的上下文碎片问题。但是,这种评估过程太过昂贵。
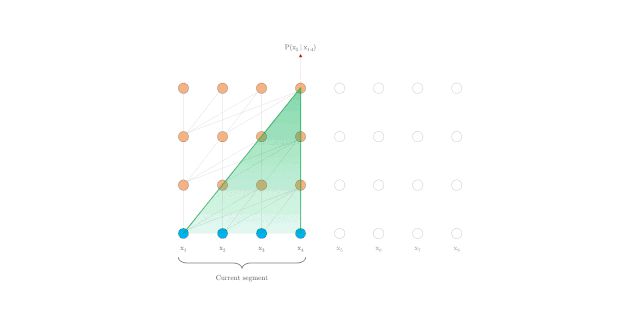 图11 动态演示: vanilla model 的评估过程[9]
图11 动态演示: vanilla model 的评估过程[9]
这里我们先来看 Transformer-XL 中的片段循环机制。引入循环机制,在训练过程中,前一片段中的隐藏状态序列(每一层都)会被固定并缓存,以便在处理下一片段时使用其作为「扩展上下文」。如图 12.a 所示,绿色部分表示当前片段使用的扩展上下文。对于每一层而言,输入为前一片段以及当前片段的前一层的输出,从而可以保证对长期依赖的建模能力并避免了上下文碎片问题(图 13)。
图12 Transformer-XL 模型训练与评估流程可视化(片段长度为 4)
图13 动态演示: Transformer-XL 的训练过程[9]
下面用公式表达上述过程。第 ???? 与 ????+1 个长度为 L 的连续片段表示为![]() ,由
,由![]() 生成的第 n 层隐藏状态序列称为
生成的第 n 层隐藏状态序列称为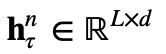 ,那么
,那么![]() 的计算过程如下:
的计算过程如下:
其中,![]() 表示 stop-gradient 函数,
表示 stop-gradient 函数,![]() 表示沿长度维度将两个隐层状态序列进行连接,W 表示模型参数。第一行公式得到包含扩展上下文的
表示沿长度维度将两个隐层状态序列进行连接,W 表示模型参数。第一行公式得到包含扩展上下文的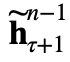 作为新的输入,第二行与 vanilla Transformer 中类似,只是 key 和 value 均使用
作为新的输入,第二行与 vanilla Transformer 中类似,只是 key 和 value 均使用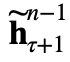 。
。
借助片段循环机制,可以使隐藏状态做到片段级循环,这实际上使得有效的上下文可以远远超过两个片段。注意,这里的![]() 之间的循环依赖是每段向下移动一层的,这与 RNN-LM 中的同一层循环是不同的。因此,最大可能依赖长度是关于层数和片段长度线性增长的(例如
之间的循环依赖是每段向下移动一层的,这与 RNN-LM 中的同一层循环是不同的。因此,最大可能依赖长度是关于层数和片段长度线性增长的(例如![]() ),如图 12.b 中的阴影区域所示。
),如图 12.b 中的阴影区域所示。
采用片段循环机制,不仅可以获得更长的上下文从而解决上下文碎片问题,而且可以加快评估速度。在评估过程中,XL 可以重复使用先前片段中的表示,不需要像 vanilla model 那样重新计算(图14)。最后,理论上讲,可以在 GPU内存允许的范围内缓存尽可能多的片段作为扩展的上下文,并将可能跨越了多个片段的旧隐藏状态称为 Memory ![]() 。在论文的实验中,M 在训练时设置为片段长度,评估过程中则会增加。
。在论文的实验中,M 在训练时设置为片段长度,评估过程中则会增加。
图14 动态演示: Transformer-XL 的评估过程[9]
在借助上述文字充分理解片段循环机制后,再来看为了在 Transformer 中实现这一机制而提出的 Relative Positional Encodings。
在片段循环机制中,有一个重要问题没有得到解决:如何保证在循环时,位置信息的连贯性?具体而言,vanilla Transformer 中使用 positional encodings 获得 ,其第 i 行
,其第 i 行![]() 表示的是片段内的绝对位置 i ,
表示的是片段内的绝对位置 i ,![]() 则规定了建模的最大长度。之后将单词嵌入和位置编码逐元素相加,如果直接在片段循环机制中使用如上位置表示方式,那么隐藏状态序列的计算过程如下:
则规定了建模的最大长度。之后将单词嵌入和位置编码逐元素相加,如果直接在片段循环机制中使用如上位置表示方式,那么隐藏状态序列的计算过程如下:
其中,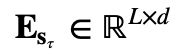 是序列
是序列![]() 的词嵌入表示,f 表示变换函数。此时,无论是
的词嵌入表示,f 表示变换函数。此时,无论是![]() 还是
还是 都使用同样的位置编码
都使用同样的位置编码 。因此,对于任意
。因此,对于任意![]() ,模型没有任何信息能用来区分
,模型没有任何信息能用来区分 和
和![]() 之间的位置差异,从而导致了性能损失。
之间的位置差异,从而导致了性能损失。
为了避免上述问题的出现,论文提出了仅在隐藏状态中对相对位置信息进行编码。
Conceptually, the positional encoding gives the model a temporal clue or “bias” about how information should be gathered, i.e., where to attend.
从概念上讲,位置编码为模型提供了关于如何理解信息(关注哪里)的时间线索或时间偏差/倾向。为此,可以在每一层的 attention score 中引入相同的信息,而不是将 “bias” 静态放入初始嵌入中。更重要的是,以相对方式定义的时间偏差是更为直观和可概括的。例如,查询向量 和键向量
和键向量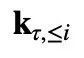 运算时,并不需要知道每个键向量的绝对位置来分辨其时间顺序,只要知道每个
运算时,并不需要知道每个键向量的绝对位置来分辨其时间顺序,只要知道每个 和
和 之间的相对距离即可,即 i-j。
之间的相对距离即可,即 i-j。
因此,可以创建一组相对位置编码![]() ,
,![]() 表示的是相对距离为 i 时的情况。将相对距离动态引入至 attention score 中,使查询向量可以分辨
表示的是相对距离为 i 时的情况。将相对距离动态引入至 attention score 中,使查询向量可以分辨 和
和![]() 之间的位置差异,从而使片段循环机制有效。另外,作者认为这样不会损失任何时间信息,因为可以从相对位置递归地得到绝对位置。
之间的位置差异,从而使片段循环机制有效。另外,作者认为这样不会损失任何时间信息,因为可以从相对位置递归地得到绝对位置。
为了理解如何动态引入相对位置信息,我们首先将同一片段内的![]() 与
与 之间的注意力得分(即 RPR 中的
之间的注意力得分(即 RPR 中的![]() )分解为:
)分解为:
Transformer-XL基于仅依赖相对位置信息的思想,提出如下改动:
下面对改动进行一一解释。
首先将 (b), (d) 中用于计算键向量的绝对位置编码
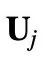 替换为相对位置编码
替换为相对位置编码 。注意这里的 R 不是可学习的,而是和 vanilla Transformer 中类似的正弦编码矩阵,只要将其公式中的 pos 替换为 i-j 即可。(这里的
。注意这里的 R 不是可学习的,而是和 vanilla Transformer 中类似的正弦编码矩阵,只要将其公式中的 pos 替换为 i-j 即可。(这里的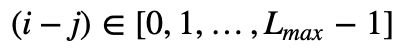 ,因为模型是自回归的)
,因为模型是自回归的)接着引入可训练参数
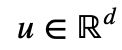 来代替 (c) 中原来的
来代替 (c) 中原来的 ,这使得所有查询位置 i 的查询向量都是相同的,所以不管查询位置是什么,对不同单词的注意偏差都是相同的。类似的,引入
,这使得所有查询位置 i 的查询向量都是相同的,所以不管查询位置是什么,对不同单词的注意偏差都是相同的。类似的,引入 来代替 (d) 中的
来代替 (d) 中的  。
。
Transformer-XL 认为此时的公式中的每一项都尤其直观含义:
(a) 表示基于内容的处理(content-based addressing)
(b) 表示基于内容的位置偏差(content-dependent positional bias)
(c) 表示整体内容偏差(global content bias)
(d) 表示整体位置偏差 (global positional bias)
与 RPR 相比,RPR 仅仅只有 (a) 与 (b) 两项,并且将 合并为可训练的矩阵
合并为可训练的矩阵 ,这放弃了 vanilla Transformer 中的正弦位置编码中内置的归纳偏置。相反,Transformer-XL的 R 很好地保留了归纳偏置,并且获得了能够将基于定长 memory 训练的模型在评估时自动泛化至更长的 memory 的好处。
,这放弃了 vanilla Transformer 中的正弦位置编码中内置的归纳偏置。相反,Transformer-XL的 R 很好地保留了归纳偏置,并且获得了能够将基于定长 memory 训练的模型在评估时自动泛化至更长的 memory 的好处。
结合上述两种机制,就得到了 Transformer-XL 的体系结构。对于一个单注意力头的 N 层 Transformer-XL 而言,对于 :
:
这里需要补充的是,Transformer-XL 所采用的相对距离表示方法是不具有方向性的,即![]() ,做的是自回归的语言建模任务;而 RPR 中采用的相对距离是具有方向性的,做的机器翻译任务。不过其实由于
,做的是自回归的语言建模任务;而 RPR 中采用的相对距离是具有方向性的,做的机器翻译任务。不过其实由于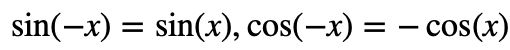 ,(i-j) 的定义域变为例如
,(i-j) 的定义域变为例如![]() 时,
时, 其实是可以为 attention score 带来方向信息的[4]。
其实是可以为 attention score 带来方向信息的[4]。
4. Complex Embeddings
上述两篇工作都是从 Attention 计算的角度出发,尝试在计算点积时融入相对位置信息。而 Encoding word order in complex embeddings[11] 一文则从单词嵌入和位置嵌入相结合的角度出发,设计了关于位置变量的连续函数,并扩展到了复数域,获得了更丰富的表示。
Complex Embbdeeings 一文认为,当前的神经网络使用位置嵌入来对单词位置进行建模,问题在于位置嵌入捕获单个单词的位置,而不捕获单词位置之间的有序关系(例如相邻或前序)。例如 ConvSeq 中的位置嵌入假设单个单词位置是独立的,并且不考虑相邻单词位置之间的关系。作者认为,单词的全局绝对位置及其内部顺序和相邻关系在语言上都是至关重要的。这一点也在 RPR 和 Transformer-XL 两篇文章中有提及,展示了对序列元素之间的距离进行建模的重要性,并明确使用额外的相对位置编码来捕获单词的相对距离关系。文中提出的解决方案,将以前定义为独立向量的词嵌入,推广为关于位置变量的连续函数。位置变量的连续函数的好处是单词表示会随着位置的增加而平滑地移动。因此,处于不同位置的单词表示可以以连续函数彼此相关。为了更丰富的表示,这些函数的通用解决方案扩展到了复数值域。
首先,词嵌入 WE 通常定义为一个将离散的词索引映射到一个 D 维实值向量的映射函数![]() 。
。
类似的,位置嵌入 PE 定义了另一个将一个离散的位置索引映射到一个向量的映射函数 。单词
。单词![]() (给定词表
(给定词表![]() 中的第 j 个词)在一个句子的 pos-th 位置时的最终嵌入通常通过求和来构建:
中的第 j 个词)在一个句子的 pos-th 位置时的最终嵌入通常通过求和来构建:
由于单词嵌入映射![]() 和位置嵌入映射
和位置嵌入映射![]() 仅将整数值用作单词索引或位置索引,单个单词或位置的嵌入矢量是单独训练的。每个单词向量的独立训练是合理的,因为单词索引基于给定任意词汇的顺序,并且不捕获与其相邻单词的任何特定顺序关系。
仅将整数值用作单词索引或位置索引,单个单词或位置的嵌入矢量是单独训练的。每个单词向量的独立训练是合理的,因为单词索引基于给定任意词汇的顺序,并且不捕获与其相邻单词的任何特定顺序关系。
但是,位置索引捕获了一个有序的关系,例如相邻关系或前序关系,现在的做法导致在各个位置上位置嵌入是相互独立的。位置之间的有序关系未建模。作者将此称为位置独立性问题 (position independence problem)。
在位置不敏感的神经网络中使用位置嵌入时,此问题变得尤为重要,例如FastText,ConvSeq和Transformer,因为它对于具有原始位置嵌入的对位置不敏感的神经网络而言,很难推断出位置pos的
接近位置pos+1的
,或者
在
之前(即之前提到相邻或前序);相反,只能推断
和
位于不同的位置,而它们之间的相对距离几乎是未知的。因此,原始位置嵌入无法完全捕捉语言的顺序方面。
在等式 (5) 里的通用定义中,每个维度的位置嵌入是基于离散位置索引 {0, 1, 2, …, pos, …} 获得的。这使得很难建模位置之间的有序关系。该问题的一种解决方案是在位置索引上构建连续函数,以表示特定单词的单个维度。形式上,我们将通用嵌入定义为:
其中![]() 是
是![]() 的缩写,表示关于位置索引 pos 的 D 个函数,而
的缩写,表示关于位置索引 pos 的 D 个函数,而![]() 是从单词索引到 D 个函数的映射。那么 pos 位置的单词
是从单词索引到 D 个函数的映射。那么 pos 位置的单词![]() 的D维向量表示可以扩展写为:
的D维向量表示可以扩展写为:
其中 是位置索引 pos 在复数域上的函数(下文在不混淆的情况下会将
是位置索引 pos 在复数域上的函数(下文在不混淆的情况下会将![]() 简写为 g )。此时要将单词
简写为 g )。此时要将单词![]() 从当前位置 pos 移动到另一个 pos’,只需将变量 pos 替换为 pos’,而无需更改
从当前位置 pos 移动到另一个 pos’,只需将变量 pos 替换为 pos’,而无需更改![]() 。
。
上述函数应当满足以下属性:
位置无关的偏移转换 (Position-free offset transformation) :
有界性 (Boundedness) :
为了降低难度,作者假设变换函数![]() 是线性变换。随后证明了在复数域上,函数
是线性变换。随后证明了在复数域上,函数![]() 是有界并且线性证明的位置无关的偏移转换,当且仅当
是有界并且线性证明的位置无关的偏移转换,当且仅当![]() (推导参见原文)。
(推导参见原文)。
那么对于任意![]() ,结合欧拉公式,我们可以写成
,结合欧拉公式,我们可以写成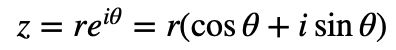 ,这里的 i 是虚数单位。因此我们有:
,这里的 i 是虚数单位。因此我们有:
一个自然且简单的避免这一问题的方法是固定![]() 。
。
因此可以简化形式写为![]() ,并且可以将 g 视为以固定周期在半径为 r 的复数圆上逆时针嵌入位置( r 是振幅项,θ 是初始相位项,
,并且可以将 g 视为以固定周期在半径为 r 的复数圆上逆时针嵌入位置( r 是振幅项,θ 是初始相位项,![]() 是频率,
是频率,![]() 是周期)。
是周期)。
那么现在我们可以定义复数域词嵌入 g 是从词索引 j 和词位置索引 pos 到![]() 的映射。对于在位置 pos 的单词
的映射。对于在位置 pos 的单词![]() ,通用复数域嵌入被定义为
,通用复数域嵌入被定义为![]() 的 D维向量,代入公式 7 扩展为:
的 D维向量,代入公式 7 扩展为:
在图15中,每个维度都表示为一个波,该波由振幅,周期/频率和初始相位参数化。嵌入的可训练参数是振幅向量![]() ,周期或频率相关的权重
,周期或频率相关的权重![]() 和初相向量
和初相向量![]() 。
。
图15 (单个单词在不同位置的 3维 复数嵌入。三个波函数(将初始相位设置为零)显示了嵌入的实部;虚部具有π/2的相位差,并显示与实值对应的相同曲线。x 轴表示单词的绝对位置,y 轴表示单词向量中每个元素的值。颜色标记了嵌入的不同维度。函数和每条垂直线之间的三个交叉点(对应于特定位置pos)表示该单词在第pos个位置的嵌入。) 本图用三维复数值嵌入说明了这种类型的单词表示,其中振幅{r1, r2, r3}表示对应于经典单词向量的语义方面,而周期{p1, p2, p3}表示这个词对位置信息有多敏感。
我们可以观察到:
所有位置上的
 的平均值与振幅嵌入线性相关。
的平均值与振幅嵌入线性相关。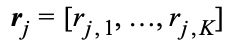 并且振幅嵌入
并且振幅嵌入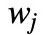 只依赖于单词(和维度 d ),而不是单词的位置,那么我们可以将向量
只依赖于单词(和维度 d ),而不是单词的位置,那么我们可以将向量 视为“纯”位置嵌入。因此,我们的复数嵌入可以被视为单词嵌入
视为“纯”位置嵌入。因此,我们的复数嵌入可以被视为单词嵌入 与位置嵌入
与位置嵌入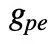 之间的逐元素乘法:
之间的逐元素乘法:周期/频率确定单词对位置的敏感程度:在极长的周期内(即
 非常小),对于所有可能的 pos 值,复数值嵌入近似恒定,因此近似于标准词嵌入。相反,如果周期短,则嵌入将对位置参数高度敏感。
非常小),对于所有可能的 pos 值,复数值嵌入近似恒定,因此近似于标准词嵌入。相反,如果周期短,则嵌入将对位置参数高度敏感。
那么可以认为,不同于以往对位置嵌入进行的加性操作,作者将单词嵌入和位置嵌入通过逐元素乘法在某种程度上解耦,因此频率/周期项(与![]() 有关)可以自适应地调整每个单词和每个单词的语义和位置信息之间的重要性尺寸。
有关)可以自适应地调整每个单词和每个单词的语义和位置信息之间的重要性尺寸。
此外,原文中还描述了降低参数量的技巧,以及如何在 CNN、RNN 和 Transformer 中使用 Complex Embeddings。在附录中,还介绍了与原始 Transformer 位置嵌入的关系。
5. 小结与展望
本文主要对原始 Transformer[1]、RPR[2]、 Transformer-XL[3] 以及 Complex Embeddings[11]中使用的位置表示方法,进行了较为详细的介绍。从最初的绝对位置编码与单词嵌入相加作为第一层的输入,再到 RPR 提出直接在注意力分数的计算中引入相对位置信息,并学习相对距离的表示矩阵(长度固定),再到 Transformer-XL 中引入偏置信息,并重新使用 Transformer 中的编码公式生成相对距离的表示矩阵,使长度可泛化,最后到 Complex Embeddings 中通过复数域的连续函数来编码词在不同位置的表示。
我们可以将 BERT 中使用的 Learned Positional Embedding(LPE),Sinusoidal Position Encoding(SPE),RPR 以及 Complex Embeddings(CE) 进行对比:
从可解释性/可理解性上来说,我认为后三者基于公式构造的方式是优于 LPE 的,尤其是 CE 通过优美的数学证明为我们提供了表示能力更好的复数域表示,并且语义信息和位置信息的重要性尺寸是自适应学习的。
CE 还在附录中证明了其特定情况与Transformer 使用的位置编码之间存在直接的联系。
从可扩展性上来说,后三者的可扩展性优于 LPE,因为 LPE 受限于最大序列长度,一旦需要扩展到更长的序列上,就必须重新训练。
从参数量上来说,LPE 的参数量与其设置的最大序列长度线性相关,SPE 与 RPR不会引入额外的参数,而 CE 在不进行参数优化时的参数量是原 Word Embedding 的三倍。
从实验效果上来说,在 SPE 提出后,Transformer 原文表示 LPE 和 SPE 的效果并无明显差别,而后续工作也基本是结果导向的。
CE 则通过在文本分类,机器翻译和语言建模上的的实验,证明其相较于先前的工作有着明显的提升。
实际使用中,大家可以尝试相关的实验。
那么未来,我们还需要对位置表示做怎样的工作呢?比如目前位置信息的定义仅限于绝对位置与相对位置,而类似句法信息这样细粒度、结构化的依存句法信息和语义依存信息,是作为外部知识引入的,并且已经有很多工作通过设计 Probe 任务,证明了 ELMo、BERT 等模型学习得到的表示,隐式建模了句法信息等信息。有没有可能在位置信息中直接引入类似的先验信息,帮助模型在对这些先验信息敏感的任务上取得更好的结果呢?
让我们拭目以待~
参考文献
[1] Vaswani, Ashish et al. “Attention is All you Need.” NIPS (2017). https://arxiv.org/abs/1706.03762
[2] Shaw, Peter et al. “Self-Attention with Relative Position Representations.” NAACL-HLT (2018). https://arxiv.org/abs/1803.02155
[3] Dai, Zihang et al. “Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context.” ACL (2019). https://arxiv.org/abs/1901.02860
[4] Yan, Hang et al. “TENER: Adapting Transformer Encoder for Named Entity Recognition.” ArXiv abs/1911.04474 (2019): n. pag. https://arxiv.org/abs/1911.04474
[5] Gehring, Jonas et al. “Convolutional Sequence to Sequence Learning.” ArXiv abs/1705.03122 (2017): n. pag. https://arxiv.org/abs/1705.03122
[6] Devlin, Jacob et al. “BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding.” ArXiv abs/1810.04805 (2019): n. pag. https://arxiv.org/abs/1810.04805
[7] How self-attention with relative position representations works https://medium.com/@_init_/how-self-attention-with-relative-position-representations-works-28173b8c245a
[8] Al-Rfou, Rami et al. “Character-Level Language Modeling with Deeper Self-Attention.” AAAI (2019). https://arxiv.org/abs/1808.04444
[9] Google AI Blog https://ai.googleblog.com/2019/01/transformer-xl-unleashing-potential-of.html
[10] Transformer Architecture: The Positional Encoding https://kazemnejad.com/blog/transformer_architecture_positional_encoding/#what-is-positional-encoding-and-why-do-we-need-it-in-the-first-place
[11] Wang, Benyou et al. “Encoding word order in complex embeddings.” ArXiv abs/1912.12333 (2019): n. pag. https://openreview.net/forum?id=Hke-WTVtwr
本期责任编辑:丁 效
本期编辑:顾宇轩
投稿或交流学习,备注:昵称-学校(公司)-方向,进入DL&NLP交流群。
方向有很多:机器学习、深度学习,python,情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。
![]()
记得备注呦
![]()
让更多的人知道你“在看”
![]()