概率图-表示-贝叶斯网络

一、贝叶斯网例子

贝叶斯网是一种经典的概率图模型，它利用有向无环图来刻画属性之间的依赖关系。

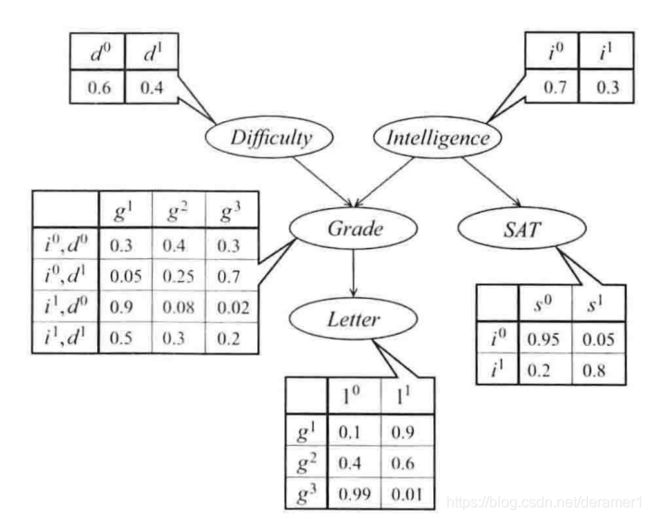
首先来看一个的例子，一个学生想要请求教授为其写一封推荐信，推荐信的质量用变量L表示，取值范围为{是,否}。而教授健忘不知道这个学生的名字，所以要查看学生的成绩来确定是否为其写推荐信。学生成绩的取值范围为{A,B,C}，分别对应于g1,g2,g3，而考试的成绩和试题的难度还有智商有关系，他们的取值范围都是两个，还有一个SAT成绩作为辅助评判标准。

试题难度D：{d1(难)，d0(简单)}

智商高低I：{i1(高智商)，i0(低智商)}

成绩G：{A,B,C}

SAT成绩S:{s1(高分)，s0(低分)}

推荐信质量L:{l1(是)，l0（否)}

直接对上面的信息进行建模，写出他们的联合概率分布表，这个联合概率分布表的大小为2*2*3*2*2=48种，可以发现这个数目巨大。假设有K个变量，每一个变量的取值为N个，则最后联合概率分布表的大小为N^K，数目巨大根本无法进行建模。

这个时候需要对上面的联合概率进行化简，首先想到的就是朴素贝叶斯算法中方法，假设各个特征独立，那么联合概率分布就可以写成独立变量的乘积，，这样只需要确定2+2+3+2+2=11个变量就可以了，然而在现实生活中，各个特征独立的假设太强。例如，试题难度越高，取得成绩越高的可能性就越低，这两个变量之间明显不是独立的。所以，这个时候贝叶斯网就出来了。

贝叶斯网利用箭头方向来表示影响关系，如下图所示，试题难度和智商会影响成绩，而成绩的高低会影响推荐信的质量，智商的高低还会影响SAT的分数。这样建模看起来就比较合理。

 

                           

则上面的模型可以表示为:

既一个贝叶斯网可以分解为各个节点的条件概率分布乘积，这个称为贝叶斯网的链式法则。par(Xi)是x的父节点的集合。

                                                   

这样我们需要建模的参数就比较少，同时也符合实际。下面我们来计算一下在试题难度简单，智商高，SAT成绩和考试成绩都高的情况下，拿到推荐信的概率。

                                  =0.6*0.3*0.9*0.8*0.9

                                  =0.11664

那么为什么一个贝叶斯网可以分解成上面的形式呢，这就要设计到条件独立性原理。

二、概率影响的流动性及条件独立

2.1 概率影响流动性的感性认识

为了解释上面的式子，首先要了解概率影响的流动性。

首先，要看看上图，左边表示的是影响，W属于Z表示的是W已经被观测了，W不属于Z表示的是W没有被观测。某一项打√表示的是X,Y相互影响，打×表示X，Y不影响，相互独立。

对于第一种情况，当W没有被观测的时候，X,Y是相互影响的，当W被观测了，X，Y就独立了。以I->G->L为例，当G没有被观测的时候，我们认为一个高智商的学生会在考试中得到A的可能性比较大，进而会得到推荐信。而一旦G被观测了，那么一个学生智商高低和是否得到推荐信就没有关系了，如果G为A，那么这个时候即使智商低，得到推荐信的可能性比较大。

第二种情况和第一种情况类似，这里就不说了。

第三种情况，当W没有被观测的时候，X,Y之间有关系。当W被观测了，X,Y之间就没关系了。以G<-I->S为例，当I没被观测时，比如SAT取得高分，那么认为他智商高的概率大，进而认为Grade取得高分的概率比较大。而一旦I被观测了，SAT和Grade就不相互影响了。比如智商高，SAT分低，那么Grade的分可能高，因为可能SAT考试中没有发挥好。

第四种情况，当W没有被观测的时候，X,Y独立，当W被观测到了，则X,Y有关系，这个和前面的正好相反。以I->G<-I为例，在没有观测到G时，试题难度和智商没有什么关系，而一旦G被观测到了，例如，G高，那么试题难度和智商就有关系了，如果试题男，取得分高的情况下，那我们认为智商大概率下很高。

2.2  条件独立定义

有效迹：对于贝叶斯网络中的一条路径，如和观测变量子集Z，当X1，Xn能相互影响的时候，称路径是有效的。

条件独立：当不是有效迹的时候，X1和Xn条件独立。

d-分离：若图G在给定观测变量子集Z的条件下，节点X和Y之间不存在任何有效迹，则称X和Y在给定Z的时候是d-分离的。记为

条件独立：如果概率图G满足,则称X与Y条件独立。

定理：父节点已知时，该节点和其所有的非后代节点条件独立。

2.3 条件独立性对因为分解的证明

我们把上面的贝叶斯网络分解成如下的形式：

将上面的式子展开成条件概率的形式

对比上面两个式子，要想上面的两个式子成立，则要求：

即父节点已知的时候，该节点和其所有的非后代节点条件独立。上面的定理证明完毕。

 

参考资料： 1>机器学习-白板推导-概率图

                    2>Daphne Koller,Nir Fridman著，王飞跃,韩素青译-概率图模型原理技术

                    3>Coursera 课程Probabilistic Graphical Models