《自抗扰控制技术》——第二遍(仿真)
目录
- 感想
- 复现书上的仿真图像
-
- 第一章:剖析经典PID调节器
- 第二章:跟踪微分器
- 第三章:非光滑反馈的功能和效率
- 第四章:扩张状态观测器
- 第五章:自抗扰控制器
- 第六章:自抗扰控制器的应用
- 小结
- 参考文献
感想
第一遍阅读看的稀里糊涂的,只能努力记住一些醒目的结论。
第二遍的时候,把书上大部分的仿真图像复现了一下,大概知道怎么用了(果然是看一遍不如抄一遍啊),也更加直观地体会到ADRC各个部分的功能和威力!( 其实也不太确定搭的模型是否正确,至少大部分仿真的图线跟书上的差不多吧…)
PS:MATLAB(2015b)的模型放在最后,正在研究韩京清教授ADRC算法的朋友可以拿去参考,希望大家多提意见,分享调试经验!
复现书上的仿真图像
第一章:剖析经典PID调节器
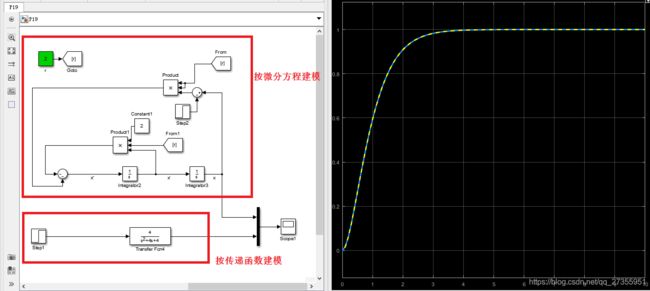
输入单位阶跃信号v0=1时的响应。参数a1,a2取成a1 = r.r,a2 = 2.r时(r>0)时,过渡过程没有超调,且r越大,过渡时间越短!

PID调节中的P和D的增益k1和k2,相当于把上面的a1,a2改成了新的参数a1’ = a1+k1,a2’ = a2 + k2。
PS:下面两种建模方式的结果应该是一样的,对于线性系统,可以通过传递函数的方式建模,简单高效;但对于非线性的系统,视乎就只能通过微分方程的形式建模了。
为什么要引入“过渡过程”?
直接取目标值与实际值之间的误差并不完全合理。比如起始阶段的控制(如阶跃响应),会产生很大的初始冲击,导致超调。而引入“过渡过程”,能够使“快速性和超调不再对立”!
\P22:如下定义是一个合适的过渡过程
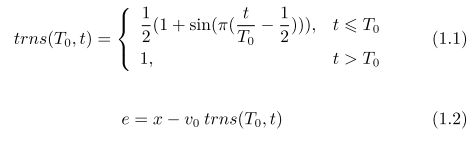
这个函数trns是在T0时间内,从0单调上升到1并保持不变的曲线

现在看看有无过渡过程的对比,控制方面只是采用P控制,当kp=6时,发现增加过渡过程还不如原来的;正如书上说的“由于安排的过渡过程和系统输出之间的误差始终都很小,要有足够的推动力启动系统,必须增益k1要足够大”,当k1取到几百,如600时,效果就出来了。


再看看控制对象变化的情况,同样取k1=600,改变传递函数的a2,分别为2, 50,0.5:

这就很能说明问题了,正如书上对安排过渡过程意义的小结:
①解决超调与快速性矛盾的一种很有效的方法
②使误差反馈增益(k1)和误差微分反馈增益的选取范围大为扩大(几百)
③使给定反馈增益所能适应的对象参数范围大为扩大(0.5-50)
P24:过渡过程的函数并不止一种,针对控制对象的不同阶,也有相应阶的过渡函数,针对二阶系统,实现PD反馈控制,再对比一、二、三阶过渡函数(按P26-27的公式一步步积分)的效果
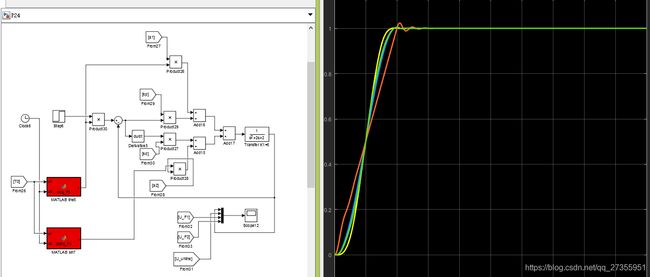
将1阶、2阶、3阶“方波”型过渡函数,分别应用到2阶对象模型上,直观上的结果:二阶的比一阶好,并且与trns_sin的非常接近!三阶的效果更好!
第二章:跟踪微分器
当输入被噪音污染时([-1,1]均匀分布的白噪声),经典微分环节的“噪声放大效应”


而换成另一种微分近似公式,用两个惯性环节并联来获取,则可以减低噪声放大效应(二阶传递函数具有较好的微分功能)

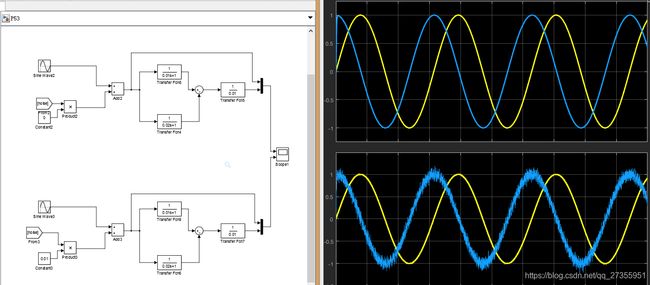
P56:用惯性环节来尽可能快地(取小的时间常数)跟踪输入信号的动态特性,通过求解微分方程(即通过积分)来获取近似微分信号。因此可以把这个动态结构称为跟踪微分器(TD)
红色部分是x2(t)与微分信号;绿色部分是x1(t)【x2的积分】与输入信号v0(t),r = 50时的情况如下图

适当加大r,能够得到更好的跟踪微分效果,那能否用最快地跟踪输入信号的动态环节来获取微分信号呢?这就引出了“以圆点为终点的快速最优控制综合函数u(x1,x2)”【涉及到最优控制理论,还没学习过】

用它则可以构建如下非线性跟踪微分器,仿真的结果,确实x1与输入信号之间看不出延迟,即“最快地跟踪输入信号”


上述最速跟踪微分器有许多很好的性能,然而直接把它离散化来进行数值计算,那么系统进入稳态后会参数不能令人满意的高频颠振,将上面模型输入的正弦信号改为阶跃信号后,能够看出问题,即微分信号不理想。如果减小r,则无法实现无超调的控制;增大r,颠振会更强烈。即“固有的高频颠振”。

为了解决这个问题,韩教授设计出了“最速控制综合函数fhan(x1,x2,r,h)”,在书上第2.7小节有详细的推导,我目前还没有能力去推导和理解,只能记下来先用

进而得到了“最速离散跟踪微分器”,

P71用它去获取上面系统的信号,r = 0.1时,不再出现高频颠振;增大r(缩小过渡时间),如r = 1时,也还是会有一些振荡;继续增大,如r=20,貌似也会出现高频颠振。所以说选择合适的r,能够使振荡被控制在一定的可接受范围内,同时实现无超调的控制。

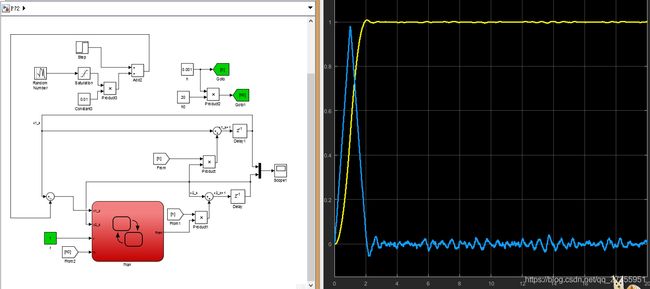
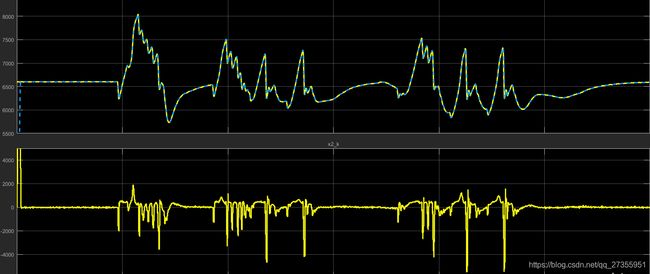
用自己的一组实验数据去作为模型的信号源输入,调整合适的r和h0,x1则能够完美的跟踪输入信号;由于没有实际微分信号的数据,所以不好对比,但看上去也是很棒的
第三章:非光滑反馈的功能和效率
\P112:先用非线性状态反馈把非线性控制系统变成纯积分器型串联线性控制系统,然后再实施状态反馈。是“直接反馈线性化”的基本思想!
那么用什么样的非线性反馈呢?P121-123:

什么是状态反馈呢?以状态变量x1,x2作为输入的反馈控制。
那么u = fhan(x1-v,cx2,r,h1)属于状态反馈,又因为计算过程中是开方运算(<1),所以为非光滑的。
P126:非光滑的误差反馈率,具有小误差大增益,大误差小增益的特点,是控制工程界追求多年的误差反馈率。
PS:第二章的fhan函数用于跟踪输入信号和微分信号,应对的是输入信号的变化以及噪声;这里fhan函数用于反馈控制,应对的是系统扰动。
P146,控制目标为v0 = 2,扰动为三部分的求和,模型中蓝色sum模块连接处,从仿真结果来看,fhan反馈控制能够很好的抑制扰动的影响,将输出稳定地控制在目标值!

对于已知或可测量的扰动,可以按上面的方案来解决,那如果无法表示出扰动呢?这就是下一章的内容了。
第四章:扩张状态观测器
\P184:根据这种外部变量的观测来确定系统内部状态变量的装置叫做状态观测器。主要目标是去完成对状态变量X的估计,即下面公式里的f(x1,x2)

P188 :只要适当选取参数 β 0 1, β 0 2 和非线性函数 g 1 (e), g 2 (e) ,状态观测器( 1.6 )对很大范围的系统( 1.5 )都能很好地估计其状态变量。
其中非线性函数多采用fal

P189 按上面的公式建立观测器的模型,这个例子没有反馈的作用,所以u=0,其中g2(e) = fal(e,0.5,0.01)。
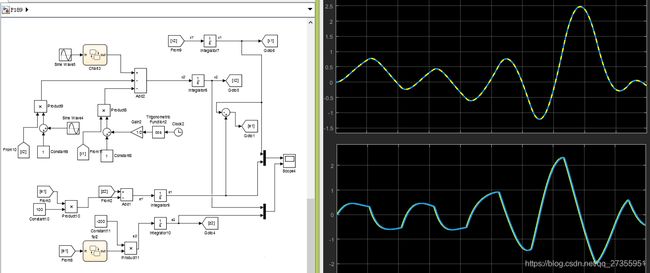
P190:改变被测系统的参数和结构,继续使用上面的状态观测器(参数结构都一样),也能够很好的观测结构,这说明“状态观测器(4.1.12)对一定范围的对象来说是完全通用的,其效率之高是由于采用了合适的非光滑函数”
PS:仿真出来的图跟书本上的不一样,没找出来问题在哪?但是拟合程度还是一样的好。

PS:这里用状态观测器(State Observer,SO)去获取原系统的输入及其微分信号,跟第二章的跟踪微分器(TD)的作用好像有点像,那么又有什么区别呢?
TD针对的是信号源(或目标值v0),侧重的是过滤噪声,获取稳定可靠的输入及其微分信号
SO针对的是控制对象,根据控制量输入u和对象的输出信号y,估计出被控对象的信息,类似于描述对象传递关系的函数 ;
P197 :我们把作用与开环系统的加速度 f(x 1 (t), x 2 (t)) 的实时作用量扩充成新的状态变量 x 3,记作 x 3 (t) = f(x 1 (t), x 2 (t)) , 建立扩张状态观测器(ESO),目标是去测量扰动w(t)。

上下两个系统相减可以得到误差方程,只要β03足够大于w,则估计误差都会足够小,那么ESO就能提炼出f(x1(t),x2(t),t,w(t)),有了扩张状态x3的估计值z3,就可以对控制量进行修改,即完成关于扰动的补偿。
看下面的图会跟直观一点

进而无论对象怎样,均可以把系统化成下图所示形式的积分器串联型控制系统,即“动态补偿线性化过程”。只要将u0设计为合适的误差反馈,则系统将很好地被控制在目标值处。而实际的控制量u,则会根据z3进行修正。
P203的例子可以更好的体会上面估计扰动的逻辑,黄色曲线是实际的f(x1(t),x2(t),t,w(t)),而蓝色的曲线是状态变量z3对其的估计值,两者几乎一样!

P205:模型中控制量放大系数b未知时,把b近似估计为b0,当作ESO的可调参数也是完全可以的。模型中δ取为5h。
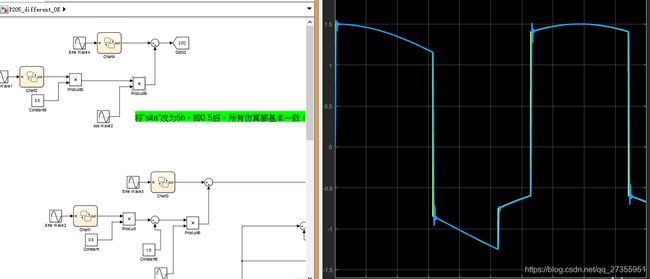
小结:
\P183:借用状态观测器的思想,把能够影响被控输出的扰动作用扩张成新的状态变量,用特殊的反馈机制来建立能够观测被扩张的状态——扰动作用的扩张状态观测,是通用而实用的扰动观测器。
\P239:估计补偿对象总和扰动来使对象变成纯积分器串联型对象的过程叫做动态补偿线性化过程,是ADRC中最关键,最核心的技术。剩下的问题就是如何对纯积分串联型对象设计好误差反馈的问题了。
这一章的内容解决了对扰动的观测,下面就是把上面所有章节汇总起来,组成ADRC的时候了!
第五章:自抗扰控制器
\P243:(1)保留经典PID的基本框架而改进其局部功能

(2)具有扰动估计、补偿能力的ADRC

P264:标准的自抗扰控制器(ADRC)算法:

上述算法对应的模型分别为:
(1)安排过渡过程

(2)估计状态和扰动
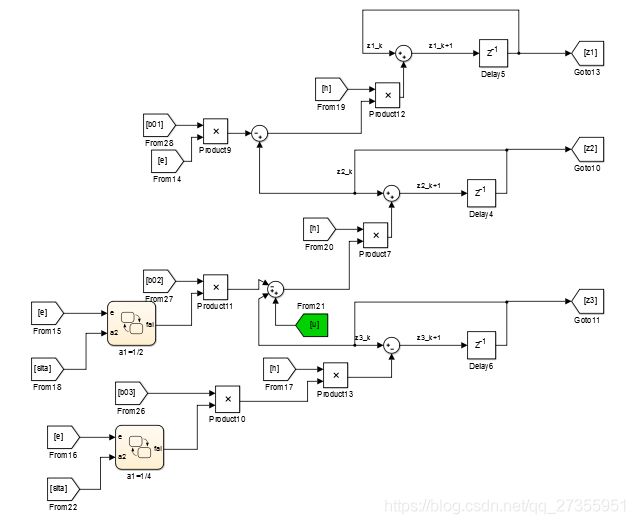
(3)误差反馈和扰动补偿

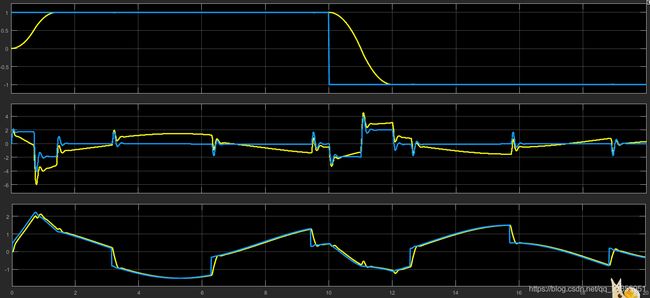
最后u作用到控制对象f(x1,x2,t)上,即使有扰动w(t),也能够实现很好的控制!第一个scope是控制目标与实际被控结果;第二个scope是u0和u;第三个scope是实际f(x1,x2,t)+w(t)和对它们的估计值z3!

\P280:分离性原理:自抗扰控制器的设计可以分成三个独立的组成部分进行设计。
第六章:自抗扰控制器的应用
\P347:技术要点
(1)搞清控输出y和控制输入u
(2)分析u的作用至少经过几个“积分器”的作用才能影响被控输出y?即所谓系统的“相对阶数”
(3)如何把作用于被控对象的各种不确定因素和扰动作用归结于为能够被估计补偿的总和扰动作用中
(4)灵活运用虚拟控制量
PS:ADRC可以应用到很多经典的控制问题上,由于我都没接触过,就暂时没有复现了…
小结
韩教授的这本书每一章节都在解决一类问题,第五章开始就是合并前四章的内容,慢慢看下来会有一种很爽的感觉!
目前电脑上仿真的结果都是非常完美的,不知道在实际应用中的表现会怎么样,要把模型转化成c代码塞到单片机里,还要一个个地调参数,实在是担心又期待!
参考文献
韩京清 . 自抗扰控制技术 : 估计补偿不确定因素的控制技术 [M]. 国防工业出版社 , 2008.
模型下载
提取码:ddcc
