吴恩达机器学习课后作业3.1——利用神经网络进行多层次分类(Multi-class Classification with the neural network)
1. 问题和数据
在练习2中,我们实现了多类逻辑回归来识别手写数字。然而,逻辑回归不能形成更复杂的假设,因为它只是一个线性分类器。
在这部分练习中,您将使用与前面相同的训练集实现一个神经网络来识别手写数字。神经网络将能够表示形成非线性假设的复杂模型。
本周,你们将使用我们已经训练过的神经网络的参数。您的目标是实现前馈传播算法来使用我们的权值进行预测。在下周的练习中,您将编写用于学习神经网络参数的反向传播算法。我们将扩展我们在练习2中写的逻辑回归的实现,并将其应用于一对一的分类。
ex3data1.mat中有5000个训练示例。其中每个训练示例是一个20像素× 20像素的数字灰度图像。每个像素都由一个浮点数表示,该浮点数表示该位置的灰度强度。20 × 20像素网格被“展开”成400维向量。每个训练示例都成为数据矩阵X中的一行。这给了我们一个5000乘400的矩阵X,其中每一行都是一个手写数字图像的训练示例。
![]()
数据集:和之前的数据集一样,数据文件是ex3data1.mat
权重集:theta的权重,数据文件是ex3weights.mat
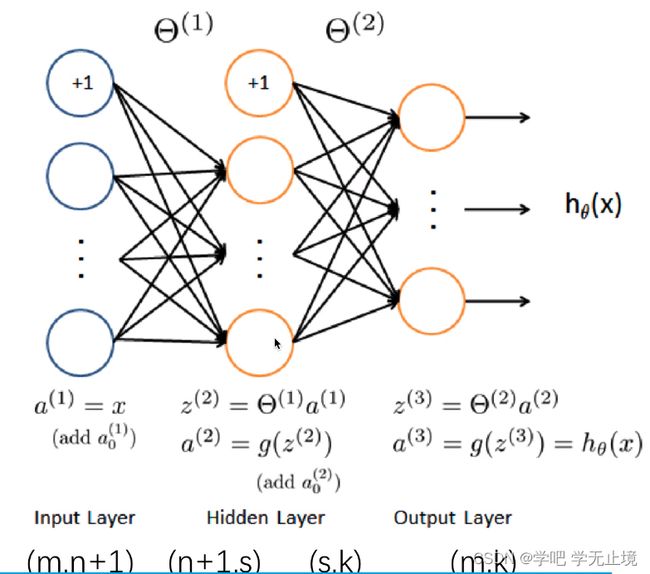
神经网络的原理主要如下图所示:
![]()
2. 数据导入与初步分析
导入包,numpy和pandas是做运算的库。
数据集是在MATLAB的格式,所以要加载它在Python,我们需要使用一个Scipy工具。
每一步都是比较容易实现的矩阵运算,需要注意的是矩阵的维度,要保证它们能做相乘运算。
import numpy as np
import scipy.io as sio
导入数据集文件,取出X和y,
# 先读取数据
data = sio.loadmat('ex3data1.mat')
raw_X = data['X']
raw_y = data['y']
将X和y改造成可以维度合适,可以参与公式运算的样子,并打印出来看一看
X = np.insert(raw_X, 0, values=1, axis=1) # 为了让X能与下面的theta1矩阵相乘,给X插入一列,loc=0,值全是1,这样X的列数就与theta1的行数
# 相同,两矩阵就能做乘法运算了
print('X.shape:', X.shape)
y = raw_y.flatten() # 把y去掉一个维度,原本y=([[1],[2],[3]...]).T的5000行1列的的样式,现在变成了y=([1,2,3....])的数组样式,从2维到1维
print('y.shape:', y.shape)
输出结果:
X.shape: (5000, 401)
y.shape: (5000,)
导入权重集文件,并打印它们的shape看看
theta = sio.loadmat('ex3weights.mat') # 这个文件数据格式是一个字典dict
print('theta.keys():', theta.keys())
theta1 = theta['Theta1']
theta2 = theta['Theta2']
print('theta1.shape:', theta1.shape)
print('theta2.shape:', theta2.shape)
打印结果:
theta.keys(): dict_keys(['__header__', '__version__', '__globals__', 'Theta1', 'Theta2'])
theta1.shape: (25, 401)
theta2.shape: (10, 26)
定义sigmoid函数:
def sigmoid(z):
return 1 / (1 + np.exp(-z))
指定a1
a1 = X
计算z2, a2,并打印a2的shape
z2 = X@theta1.T
a2 = sigmoid(z2)
print('a2.shape:', a2.shape)
输出结果:
a2.shape: (5000, 25)
为了a2和theta2能做矩阵相乘运算,将a2插入一列,并打印shape来看看
a2 = np.insert(a2, 0, values=1, axis=1) # 对X添加一列全为1的值,(X, 索引=0, 值=0, axis是按行按行插入(0:行、1:列))
print('a2.shape:', a2.shape)
输出结果:
a2.shape: (5000, 26)
计算z3, a3,并打印a3的shape
z3 = a2 @ theta2.T
a3 = sigmoid(z3)
print('a3.shape:', a3.shape)
#求准确率
y_pred = np.argmax(a3, axis=1) # arg是np中的比较函数,max是选大的意思;axis=0是行,axis=1就是将对同一行的每一列去比较,哪一个比较
# 大我们就将它的索引返回回来,比如第一个位置的结果最大,就返回它的索引,但结果是0,所以要对返回的索引加1
y_pred = y_pred + 1
acc = np.mean(y_pred == y) # 计算准确率accuracy; 求预测值y_pred等于真实值y的个数,再求平均值
print('acc:', acc)
输出的准确率挺高的:
acc: 0.9752
参考文献:
[1] https://www.bilibili.com/video/BV1mt411p7kG?p=6&spm_id_from=pageDriver
[2] https://github.com/PlayPurEo/ML-and-DL/blob/master/basic-model/3.neural%20network/nnforward.py