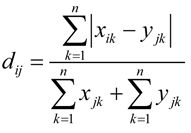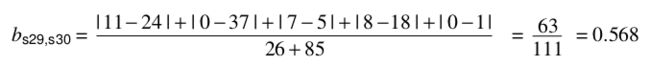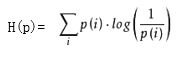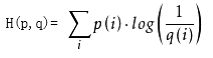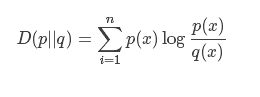机器学习领域 几种距离度量方法【3】
十三、堪培拉距离 (Canberra Distance)
十四、布雷柯蒂斯距离(Bray Curtis Distance)
十五、交叉熵(Cross Entropy)
十六、相对熵(relative entropy)
十七、js散度(Jensen-Shannon)
十八、测地距离(Geodesic distance)
堪培拉距离 (Canberra Distance)
被认为是曼哈顿距离的加权版本。
其定义公式为:
通常堪培拉距离对于接近于0(大于等于0)的值的变化非常敏感。与马氏距离一样,堪培拉距离对数据的量纲不敏感。不过堪培拉距离假定变量之间相互独立,没有考虑变量之间的相关性。
代码实现:
import numpy as np
p = np.array([11, 0, 7, 8, 0])
q = np.array([24, 37, 5, 18, 1])
n = len(p)
distance = 0
for i in range(n):
if p[i] == 0 and q[i] == 0:
distance += 0
else:
distance += abs(p[i] - q[i]) / (abs(p[i]) + abs(q[i]))
print(distance)布雷柯蒂斯距离(Bray Curtis Distance)
Bray Curtis距离主要用于生态学和环境科学,计算坐标之间的距离。该距离取值在[0,1]之间。它也可以用来计算样本之间的差异。
样本数据:
计算:
代码实现:
import numpy as np
from scipy.spatial.distance import pdist
x = np.array([11, 0, 7, 8, 0])
y = np.array([24, 37, 5, 18, 1])
# 方法一:根据公式求解
up = np.sum(np.abs(y - x))
down = np.sum(x) + np.sum(y)
d1 = (up / down)
# 方法二:根据scipy库求解
X = np.vstack([x, y])
d2 = pdist(X, 'braycurtis')
通常,一个信源发送出什么符号是不确定的,衡量它的不确定性可以根据其出现的概率来度量。概率大,出现机会多,不确定性小;反之就大。
不确定性函数f必须满足两个条件:
1)是概率P的单调递减函数;
2)两个独立符号所产生的不确定性应等于各自不确定性之和,即f(P1,P2)=f(P1)+f(P2),这称为可加性。
在信源中,考虑的不是某一单个符号发生的不确定性,而是要考虑这个信源所有可能发生情况的平均不确定性。若信源符号有n种取值:U1…Ui…Un,对应概率为:P1…Pi…Pn,且各种符号的出现彼此独立。这时,信源的平均不确定性应当为单个符号不确定性-logPi的统计平均值(E),可称为信息熵,即
假设现在有一个样本集中两个概率分布p,q,其中p为真实分布,q为非真实分布。假如,按照真实分布p来衡量识别一个样本所需要的编码长度的期望为:
但是,如果采用错误的分布q来表示来自真实分布p的平均编码长度,则应该是:
我们称H(p)为信息熵,称H(p,q)为交叉熵。
交叉熵在CNN分类中经常用到,用来作为预测值和真实标签值的距离度量。经过卷积操作后,最后一层出来的特征经过softmax函数后会变成一个概率向量,我们可以看作为是概率分布q, 而真实标签我们可以看作是概率分布p, 因此真实分布p和预测分布q的交叉熵就是我们要求的loss损失值,即
代码实现:
import numpy as np
import tensorflow as tf
fea = np.array([6.5, 4.2, 7.4, 3.5], np.float32)
label = np.array([1, 0, 0, 0])
# 方法一:根据公式求解
def softmax(x):
return np.exp(x) / np.sum(np.exp(x), axis=0)
loss1 = -np.sum(label * np.log(softmax(fea)))
# 方法二:调用tensorflow深度学习框架求解
sess = tf.Session()
logits = tf.Variable(fea)
labels = tf.Variable(label)
sess.run(tf.global_variables_initializer())
loss2 = sess.run(tf.losses.softmax_cross_entropy(labels, logits))
sess.close()
相对熵(relative entropy)
又称为KL散度(Kullback–Leibler divergence,简称KLD),信息散度(information divergence),信息增益(information gain)。
相对熵是交叉熵与信息熵的差值。即相对熵=交叉熵-信息熵 KL(p||q)=H(p,q)-H(p
表示用分布q模拟真实分布p相比用p模拟p,所需的额外信息。
相对熵(KL散度)有两个主要的性质。如下
(1)尽管 KL 散度从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,即
(2)相对熵具有非负性
![]()
总结一下:
信息熵公式:
交叉熵公式:
![]()
相对熵公式:
三者的关系:
使用场景:文本的相似度、推荐系统、用户画像…
代码实现:
import numpy as np
import scipy.stats
p = np.asarray([0.65, 0.25, 0.07, 0.03])
q = np.array([0.6, 0.25, 0.1, 0.05])
# 方法一:根据公式求解
kl1 = np.sum(p * np.log(p / q))
# 方法二:调用scipy包求解
kl2 = scipy.stats.entropy(p, q)js散度(Jensen-Shannon)
因为kl散度不具对称性,因此js散度在kl散度的基础上进行了改进,可以用于衡量两种不同分布之间的差异。
现有两个分布p1和p2,其JS散度公式为:
代码实现:
import numpy as np
import scipy.stats
p = np.asarray([0.65, 0.25, 0.07, 0.03])
q = np.array([0.6, 0.25, 0.1, 0.05])
M = (p + q) / 2
# 方法一:根据公式求解
js1 = 0.5 * np.sum(p * np.log(p / M)) + 0.5 * np.sum(q * np.log(q / M))
# 方法二:调用scipy包求解
js2 = 0.5 * scipy.stats.entropy(p, M) + 0.5 * scipy.stats.entropy(q, M)测地距离(Geodesic distance)
测地线: 流形上连接两个点的最短曲线
例如:球面上的测地线就是球面上的大圆弧
测地距离:测地线的长度