TensorFlow入门基础：单层神经网络进行函数拟合

目录

---

概要

本文介绍一个简单的人工神经网络应用实例：建立一个人工神经网络，实现对带噪声目标函数的拟合。整个过程的实现方式可以分为以下几个部分：

(1) 生成目标数据

(2) 构建网络

(3) 训练模型

(4) 模型评估

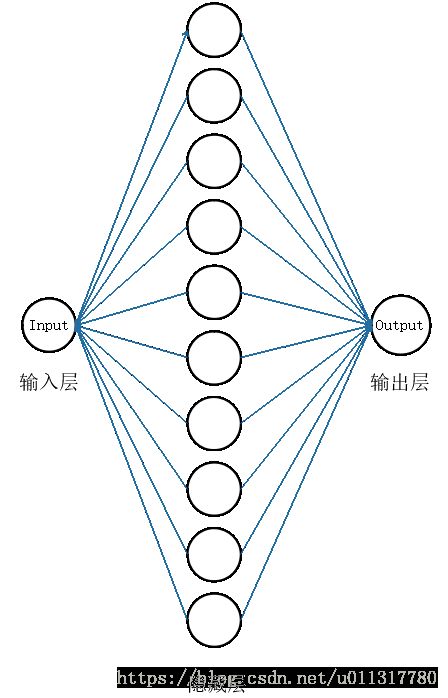
需要构建的神经网络图如下所示：

生成目标数据

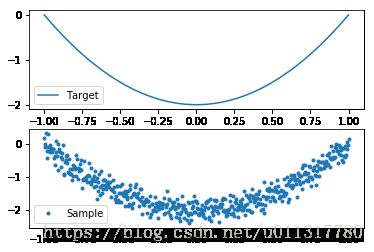
假设需要学习的方程为: $ y=2x^2-2 $，这里直接通过表达式生成目标点列，同时加入高斯白噪声：

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
x = np.linspace(-1,1,500)[:,np.newaxis]
noise = np.random.normal(0,0.2,x.shape)
fx = 2*x**2-2
y = fx + noise
subplot(2,1,1)
plot(x,fx)
legend(['Target'])
subplot(2,1,2)
plot(x,y,'.')
legend(['Sample'])
show()

下面需要定义两个不指定具体取值的占位符作为将要输入神经网络的变量：

xs = tf.placeholder(tf.float32,[None,1])
ys = tf.placeholder(tf.float32,[None,1])

构建模型

这里我们构建一个隐藏层和一个输出层。首先，定义一个函数用来添加层：

def add_layer(inputs,in_size,out_size,activation_function = None):
    weights = tf.Variable(tf.random_normal([in_size,out_size]))
    biases  = tf.Variable(tf.zeros([1,out_size])+0.1)
    Wx_plus_b = tf.matmul(inputs,weights)+biases
    if activation_function is None:
        outputs = Wx_plus_b
    else:
        outputs = activation_function(Wx_plus_b)
    return outputs

定义了add_layer()函数后，便可利用它构建神经网络的层：

# 构建具有10个隐藏层的神经元
h1 = add_layer(xs,1,10,activation_function = tf.nn.relu)
# 构建具有一个神经元的输出层
prediction = add_layer(h1,10,1,activation_function = None)

下面定义损失函数，整个算法的目的就是寻找一组weights和biases使得损失函数最小化。损失函数通常可以定义为实际值和预测值的均方误差绝对值，学习率是一个超参数，这里设为0.1：

loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys-prediction),reduction_indices=[1]))
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss) # 设置学习率为0.1

训练模型

下面通过梯度下降法训练模型1000次，并实时输出损失函数的变化情况：

init = tf.global_variables_initializer()
sess = tf.Session()                      # 创建会话
record_loss = np.zeros(1000)             # 记录损失值变化
sess.run(init)                           # 初始化所有变量
for i in range(1000):
    sess.run(train_step,feed_dict={xs: x,ys: y})
    record_loss[i] = sess.run(loss,feed_dict={xs: x,ys: y})
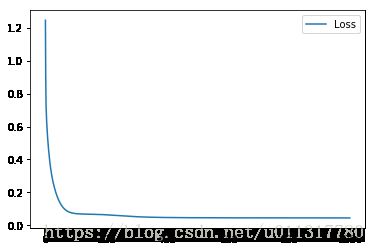
plot(record_loss)
legend(['Loss'])
show()

可以看到，经过梯度下降法1000次训练后，损失函数不断减小最后接近于0。

模型评估

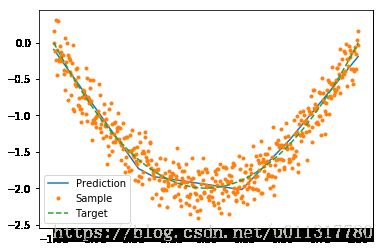
神经网络训练完成后，可以得到一组学习到的权重weights和偏置biases。将x回代到模型中，和目标曲线对比：

plot(x,sess.run(prediction,feed_dict={xs: x}))
plot(x,y,'.')
plot(x,fx,'--')
legend(['Prediction','Sample','Target'])
show()

可以发现，模型预测和目标曲线基本吻合。

参考资料

《TensorFlow技术解析与实战》——李嘉璇