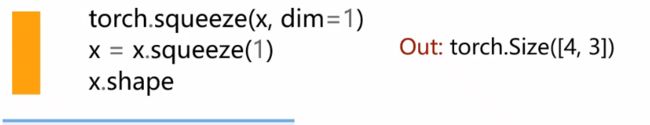PyTorch基础学习

1.tensor

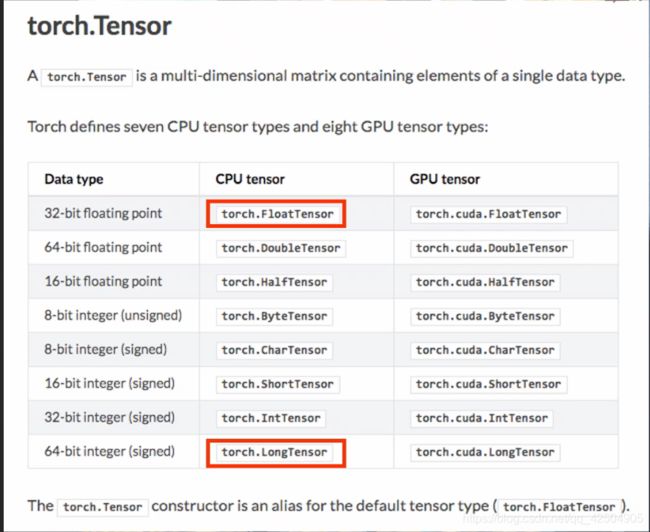
tensor中最常使用的就是FloatTensor和LongTensor，分别代表了浮点数和整型

注意：定义一个张量tensor时，T可以大写可以小写，代表的是同样的意思，但定义整型和浮点数的时候F和T一类的必须要大写

Tensor是类，是FloatTensor的别名。
tensor是函数，可根据 detype指定类别。
两者在生成0维变量时有区别。

一般情况下用tensor即可。

1.1tensor的分类

张量tensor分为0维张量1维张量二维张量和多维张量

0维张量就是标量

a = torch.tensor(2)
print(a.size())
print(a.type())

获取标量值，比如loss值

print(a.item())

结果：
torch.Size([])
torch.LongTensor
2

一维张量就是数组

a = torch.tensor([2])
print(a.size())
b = torch.tensor([2, 3, 4])
print(b.size())

torch.Size([1])
torch.Size([3])

2维张量就是矩阵

矩阵 Matrix

m1 = torch.tensor([[1, 2], [3, 4]])
print(m1.size())

m2 = torch.tensor([[1,2],
[3,4]])
print(m2.size())

torch.Size([2,2])
torch.Size([2,2])

高维张量就是低维张量的堆叠
最前面的维数表示被堆叠的 “子张量” 的数量

1.2numpy和pyTorch之间的相互转换

import numpy as np
import torch
np_arr = np.array([1,2,3,4])
tor_arr=torch.from_numpy(np_arr) # 也可直接构造 tor_arr=torch.tensor(np.array[1,2,3,4])
tor2numpy=tor_arr.numpy()
print(f’numpy:{np_arr}\ntorch:{tor_arr}\nnumpy:{tor2numpy}’)

1.3gpu tensor和cpu tensor的相互转换

注意：在gpu上的tensor如果需要转换为numpy格式，需要将gpu上的tensor先转换到cpu上再利用.numpy转换成numpy格式

1.4 tensor的高级操作

1.4.1 x.size和x.shape

x.size()表示的就是显示矩阵x的规格与x.shape表示同样的意思

1.4.2 x.view和x.reshape

矩阵的重新排列，.view（3，4）表示将之前的矩阵转换成一个3*4的矩阵，.view(12)表示将矩阵拉成一个12维的向量，但这里要注意，view操作的矩阵转换必须和之前的矩阵相匹配，比如之前是4x3的矩阵才能变成3x4矩阵，或者有12个元素，才能拉成12维的向量，在这里view和reshape功能相近，一般使用reshape即可。

1.4.3 增维操作，降维操作

增维操作

降维操作

对矩阵进行每一列的求和

1. torch.unsqueeze 详解 增维

torch.unsqueeze(input, dim, out=None)
返回一个新的张量，对输入的既定位置插入维度 1
返回张量与输入张量共享内存，所以改变其中一个的内容会改变另一个

此处dim=0代表在0维增维以此类推。

torch.squeeze降维，用法相同。

1.4.4 深拷贝、clone、detach

tensor的深拷贝（clone.detach(））
import torch
import numpy as np
a = torch.arange(6)
b = a.reshape(2,3)
print(b)
改变 b时，a也跟着改变，两者共享内容
b[0,0] = 10
print(a)

tensor([[0, 1, 2],
        [3, 4, 5]])
tensor([0, 1, 2, 3, 4, 5])

同样的这里我们加上.clone().detach()，这样得到的结果就是b与a不共享内存，改变b之后a不会随着改变。
import torch
import numpy as np
a = torch.arange(6)
b = a.reshape(2,3).clone().detach()
print(b)
改变 b时，a不跟着改变，两者不共享内容
b[0,0] = 10
print(a)
连用使用clone().detach()来复制一个跟原来张量没有任何关系的张量

tensor([[0, 1, 2],
        [3, 4, 5]])
tensor([0, 1, 2, 3, 4, 5])

tensor的深拷贝（clone）

深拷贝，拷贝后变量还可以从计算图中获取梯度信息，但requires_grad属性保持不变：
返回一个和源张量同shape、dtype和device的张量，与源张量不共享数据内存，但提供梯度的回溯。
clone操作在不共享数据内存的同时支持梯度回溯，所以常用在神经网络中某个单元需要重复使用的场景下
a = torch.arange(6)
b = a.reshape(2,3).clone()
b[0,0] = 10
print(a)
print(b)
tensor([0, 1, 2, 3, 4, 5])
tensor([[10, 1, 2],
[ 3, 4, 5]])

tensor的浅拷贝（detach）
浅拷贝，但requires_grad=False，拷贝后的张量脱离计算图：
detach的机制则与clone完全不同，即返回一个和源张量同shape、dtype和device的张量，与源张量共享数据内存，但不提供梯度计算，即requires_grad=False，因此脱离计算图。
detach操作在共享数据内存的脱离计算图，所以常用在神经网络中仅要利用张量数值，而不需要追踪导数的场景下。
b = a.reshape(2,3).detach()
b[0,0] = 10 # 数值改变了，detach共享内存
print(a)
tensor([0, 1, 2, 3, 4, 5])
tensor([[10, 1, 2],
[ 3, 4, 5]])
tensor的拷贝小结

# Operation	New/Shared memory	Still in computation graph
tensor.clone()	New	Yes
tensor.detach()	Shared	No
tensor.clone().detach()	New	No

1.4.5numel

计算tensor元素的个数，z.numel()

1.4.6item

若tensor为单元素，则返回Python的标量

1.4.7dim

查看tensor的维度x.dim

dim的不同值表示不同维度 。特别的在dim=0表示二维中的行，dim=1在二维矩阵中表示列。广泛的来说，我们不管一个矩阵是几维的，比如一个矩阵维度如下：（d0，d1,…,dn-1）,那么dim=0对应着d0，也就是第一个维度，以此类推。

知道dim的值是什么意思还不行，还要知道函数中这个dim给出来会发生什么
例子一：torch.argmax()函数中dim表示该维度会消失。
这个消失是什么意思？官方英文解释是：dim (int) – the dimension to reduce.
我们知道argmax就是得到最大值的序号索引，对于一个维度为( d 0 , d 1 )的矩阵来说，我们想要求每一行中最大数的在该行中的列号，最后我们得到的就是一个维度为( d 0 , 1 ) 的一矩阵。这时候，列就要消失了。
因此，我们想要求每一行最大的列标号，我们就要指定dim=1，表示我们不要列了，保留行的size就可以了。
假如我们想求每一列的最大行标，就可以指定dim=0，表示我们不要行了。
import torch
import os
import numpy as np
os.environ[‘CUDA_VISIBLE_DEVICES’] = ‘1’
a = torch.rand((3,4))
print(a.size())
print(a)
b = torch.argmax(a, dim=1)
print(b)
print(b.size())
输出：
torch.Size([3, 4])
tensor([[0.8338, 0.6953, 0.7558, 0.5803],
[0.2105, 0.7638, 0.0912, 0.3341],
[0.5585, 0.8019, 0.6590, 0.2268]])
tensor([0, 1, 1])
torch.Size([3])
可以看见指定dim=1时，列的size没有了。
另一个参数keepdim
keepdim=True
运算完之后的维度和原来一样，原来是三维数组现在还是三维数组（不过某一维度变成了1）；
keepdim=False
运算完之后一般少一维度，求平均变为1的那一维没有了；
默认是false，即运算完之后维度少1

1.4.8 topk

听名字就知道这个函数是用来求tensor中某个dim的前k大或者前k小的值以及对应的index。
torch.topk(input, k, dim=None, largest=True, sorted=True, out=None) -> (Tensor, LongTensor)
其中k是保留的k个值，largest=True意味着选取最大的，如果为largest为 False ，则返回最小的 k 个值。sorted=True是指将返回结果排序。

dim=1是指在列维度进行取最大，也就是寻找每一行的最大值
dim=0是指在行维度取进行最大，也就是寻找每一列的最大值 （ 有点跟逻辑反着的意思）
如果不指定dim，则默认为input的最后一维。
topk返回的是一个tuple，第一个元素指返回的具体值，第二个元素指返回值的index

2.variable

Tensor和Variable合并
torch.Tensor 和torch.autograd.Variable现在是同一个类。torch.Tensor 能够像之前的Variable一样追踪历史和反向传播。Variable仍能够正常工作，但是返回的是Tensor。所以在0.4的代码中，不需要使用Variable了。

3.pytorch的广播机制

pytorch中的广播机制和numpy中的广播机制一样, 因为都是数组的广播机制

两个维度不同的Tensor可以相乘，因为用到了广播机制

如果相加的两个数组的shape不同, 就会触发广播机制, 1)程序会自动执行操作使得A.shape==B.shape, 2)对应位置进行相加
运算结果的shape是:A.shape和B.shape对应位置的最大值,比如:A.shape=(1,9,4),B.shape=(15,1,4),那么A+B的shape是(15,9,4)
如果张量的维度不同，将维度较小的张量进行扩展，直到两个张量的维度都一样。如果两个张量在某个维度上的长度是相同的，或者其中一个张量在该维度上的长度为1，那么我们就说这两个张量在该维度上是相容的。

4.自动求导

叶子结点和非叶子节点

叶子节点：输入数据节点，没有输入箭头，只有输出箭头，程序中可用 tensor.is_leaf 来判断
叶子结点使用requires_grad参数指定是否记录梯度，方便后面使用backward方式求导。
设置成True，即进行求导。
注意：为节省计算资源，需要求导的叶子节点的 requires_grad 参数要设为 True，经过反向传播，张量的grad属性就保存了梯度。不需要计算梯度的叶子结点无需保存梯度，以便节省空间。
非叶子节点：结果节点，通过运算创建的节点，保存运算得到的数据，一定有输入箭头。

非叶子节点的操作记录在grad_fn属性中，叶子结点的grad_fn属性为None

最后得到的Tensor执行backward函数，自动计算各变量的梯度，并累加到grad属性中。计算完成后，梯度自动释放

计算图多次求导

反向传播，计算 w,b 相对 y 的梯度
y.backward()
print(f"参数 w,b 对 y 的梯度分别为：{w.grad},{b.grad}")

z.backward()
print(f"参数 w,b, 对 z 的梯度分别为：{w.grad},{b.grad}")
我们想分别求参数 （w, b） 对 y 和对 z 的导数，这时需要调用两次计算图。但，下面的代码会出错：
原因是因为pytorch是动态计算图，在每一次反向传播时，pytorch动态建立正向计算图，然后计算梯度，接着自动销毁计算图，下一次循环时，需重新建立计算图才行。这种方式非常灵活，可以动态调整训练的网络。如需多次使用同一计算图，我们可以在backward(retain_graph=True)，保持在某次反向传播后暂时保留网络不销毁。
import torch
x=torch.tensor(2.0)
w=torch.tensor(3.0, requires_grad=True)
b=torch.tensor(1.0, requires_grad=True)
构造计算图, 实现前向传播
y = torch.mul(w, x) # 等价于 w * x
z = torch.add(y, b) # 等价于 y + b
反向传播，计算 w,b 相对 y 的梯度
y.backward(retain_graph=True)
print(f"参数 w,b 对 y 的梯度分别为：{w.grad},{b.grad}")
我们利用retain_graph=True之后让第一次计算梯度之后梯度不销毁，从而我们才能第二次计算梯度。

同一计算图上第二次传播
z.backward()
print(f"参数 w,b, 对 z 的梯度分别为：{w.grad},{b.grad}")

但还有个问题，梯度是累加的，所以我们得到的结果为
参数 w,b 对 y 的梯度分别为：2.0,None
参数 w,b, 对 z 的梯度分别为：4.0,1.0
正确的结果应该是2才对，pytorch在每次反向传播后，不自动清除叶子节点的grad值，而是自动累加，方便在 batch 训练时一次把所有训练样本对损失函数的梯度加在一起，因此，梯度不需累加时，我们要手动清零

import torch
x=torch.tensor(2.0)
w=torch.tensor(3.0, requires_grad=True)
b=torch.tensor(1.0, requires_grad=True)
构造计算图, 实现前向传播
z = wx + b
y = torch.mul(w, x) # 等价于 w * x
z = torch.add(y, b) # 等价于 y + b
反向传播，计算 w,b 相对 y 的梯度
y.backward(retain_graph=True)
print(f"参数 w,b 对 y 的梯度分别为：{w.grad},{b.grad}")
手动清零 w.grad 的值
w.grad.zero_()
或者使用w.grad=torch.zeros_like(w.grad)也可以做到同样的效果。
这个地方，因为第一次计算梯度的时候我们没有计算b的梯度（b和y没有关系）所以不需要清零b的梯度。
同一计算图上第二次传播
z.backward()
print(f"参数 w,b, 对 z 的梯度分别为：{w.grad},{b.grad}")
在这里PyTorch有一个基本规定，就是只能是标量对张量求导，不能张量对张量求导
但当我们处理多任务的时候，有时候输出也是张量，此时就是张量对张量求导。
输入：n维矢量 [x1,x2,….,xn]，比如：一个目标的特征向量
输出：m维矢量， [y1,y2,….,ym]，比如：要同时完成多个任务，不同任务有不同的衡量标准
输入x对输出y求导：可以得到雅克比矩阵：

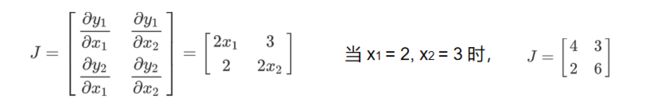
这时我们在和之前一样进行求导求梯度会报错
运行会出现错误：
grad can be implicitly created only for scalar outputs
也就是说 pytorch 默认只能对 标量 目标函数求导。
但目前目标函数是一个张量，所以需要把这个张量合成为一个代价函数，比如令代价函数为 =1+2 ，在合成的代价函数中，y1 和 y2 可以设定各自占的比例，也就是说各分代价变化时对合成代价的影响大小（即，变化率）
相当于在原有计算图的基础上再构建了一层计算图
当然如果，你认为 2 在最后的结果中比例高，也可以令 =0.21+0.82 ，此时

上面的矢量就是backward(gradient)的参数，就是在目标函数为张量时，将几个输出量合成为一个代价函数时，各输出量 在最后结果中所占的比例，也就是变化率，gradient要与输出目标函数张量同样的shape。
当给backward函数传入gradient参数时，就相当于在原有的计算图的末端，又自动添加了一个标量代价函数节点，这是我们就可以对这个计算图进行反向求导了。代码如下：
定义叶子节点 x，形状为 1x2
x = torch.tensor([[2,3]], dtype=torch.float, requires_grad=True)
结果
y = torch.zeros(1,2)
计算图
#y1 = x12 + 3*x2, y2 = x22+2*x1
y[0,0] =x[0,0] ** 2 + 3 * x[0, 1]
y[0,1] =x[0,1] ** 2 + 2 * x[0, 0]
反向传播，计算 x 对 y 的梯度

两个输出结果在最后的合成代价函数中所占的比例
y.backward(torch.tensor([[1., 1.]]))注意：这里要求gradient的shape要与目标函数张量一致，张量的内容就是各个输出量的比例
print(x.grad) # x1 相对 C=y1+y2 的梯度为 4+2=6； x2 相对 C=y1+y2 的梯度为 3+6=9
假如我们要求雅克比矩阵怎么办？

其实一样，雅克比矩阵就是要我们算出具体的每个结果，

在Antograd程序中
有两个问题：
with t.no_grad():
with是python中上下文管理器，简单理解，当要进行固定的进入，返回操作时，可以将对应需要的操作，放在with所需要的语句中。比如文件的写入（需要打开关闭文件）等。with是python中上下文管理器，简单理解，当要进行固定的进入，返回操作时，可以将对应需要的操作，放在with所需要的语句中。比如文件的写入（需要打开关闭文件）等。

在使用pytorch时，并不是所有的操作都需要进行计算图的生成（计算过程的构建，以便梯度反向传播等操作）。而对于tensor的计算操作，默认是要进行计算图的构建的，在这种情况下，可以使用 with torch.no_grad():，强制之后的内容不进行计算图构建。
如果不用with t.no_grad(),那么接下来的w和b的梯度更新就放进了训练语句里面，这样就相当于在原有神经网络之后，又继续构建网络，破坏了原有的神经网络结构。
with torch.no_grad( ) 是让节点暂时从计算图中脱离开，也就是说 其后包括的内容并不会作为计算图的一部分，而是单独计算,也就是说with torch.no_grad( ) 里的内容可以看做 是另外一个只能进行前向计算的独立的网络，可以从已创建好的网络中引用节点中的数据。 所以可以用这种方式实现网络参数的更新。

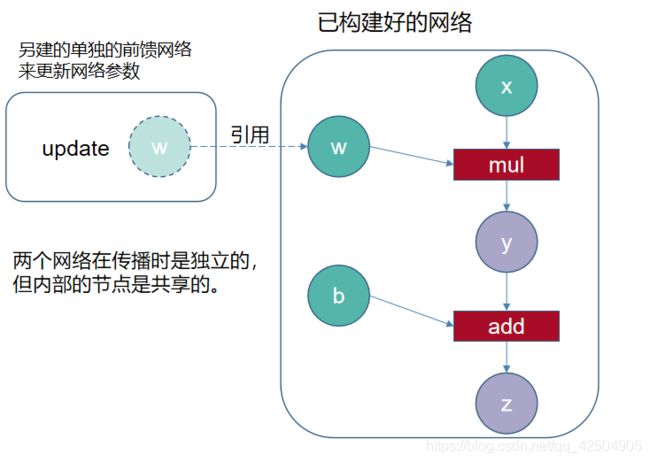
两种方法等效
使用detach( ) 可用于将网络中的某些节点的数值当常数一样引用


另一个问题：w-=lr…

这个操作叫做原位操作

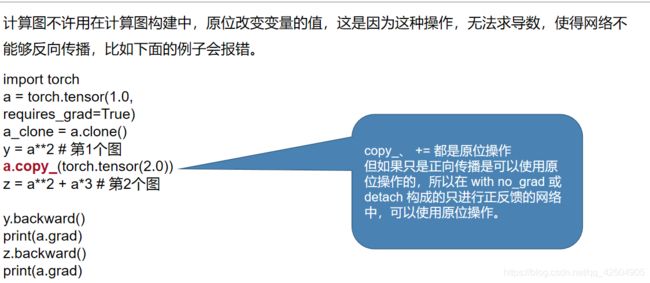
所以在with no_grad()里面可以使用原位操作
这里使用了in_place的操作
in-place operation在pytorch中是指改变一个tensor的值的时候，不经过复制操作，而是直接在原来的内存上改变它的值。可以把它成为原地操作符。
在pytorch中经常加后缀“ _ ”来代表原地in-place operation，比如说.add_() 或者.scatter()。python里面的+=，*=也是in-place operation。
这里我们使用原位操作而不使用正常的非原位操作的原因是
非原位操作实际上是开辟了新的内存空间，计算新的w.data,而原本的w.data所指向的内存地址所存放的值仍然是原来的值，但in-place赋值方式是不同的，

所以我们在计算梯度的时候，有时需要用到原位操作来不改变内存地址空间，只改变相对应的值来达到我们需要的目的。