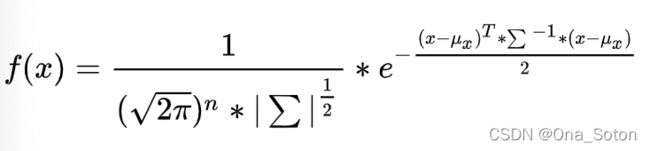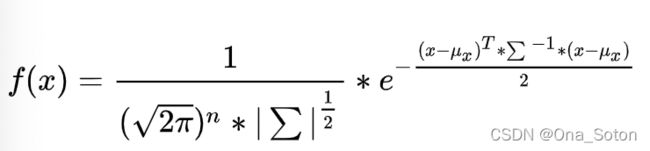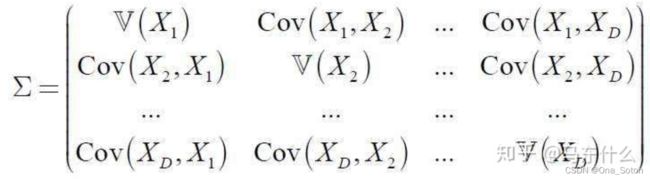一元高斯分布&多元高斯分布&高斯过程&混合高斯模型
高斯分布,又称正态分布,应用于连续型随机变量分布的模型中,对于多元高斯分布存在和一元高斯相似的,对于多元实值向量,使熵取得最大值的是高斯分布。当多个随机变量之和相加时,根据拉普拉斯提出的中心极限定理(central limit theorem),⼀组随机变量之和(当然也是随机变量)的概率分布随着和式中项的数量的增加⽽逐渐趋向⾼斯分布,在实际应用中,随着样本数量的增加,分布会迅速收敛为高斯分布,二项分布当观测次数增多时,也会趋向于高斯分布( 二项分布、泊松分布和正态分布的区别及联系? - 知乎)。
首先,明确一元高斯分布的公式为:
一个y(也就是f(x))对应一个维度的x,当一元高斯分布拓展到多元高斯分布时,也就是多个x(x1,x2,x3……)意味着多个维度,也就意味着多个特征。
我们假设了多元高斯分布的各个维度之间,也就是各个x变量之间是相互独立的,在这个假设条件下,独立的多元高斯分布公式为:
其中:
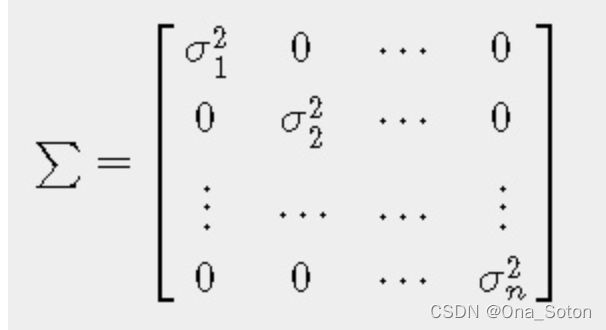 代表变量X的协方差矩阵,i行j列的元素值表示xi于xj的协方差(注意:协方差矩阵其实可以理解为表示变量之间关系的表达,因为这里假设变量之间是相互独立的,因此只有对角线上的元素值是不为0的)
代表变量X的协方差矩阵,i行j列的元素值表示xi于xj的协方差(注意:协方差矩阵其实可以理解为表示变量之间关系的表达,因为这里假设变量之间是相互独立的,因此只有对角线上的元素值是不为0的)
此外,协方差矩阵是一个实对称阵。
如果不同维度之间存在着关联,则称为相关多元正态分布,表示为:
它的表示和独立多元高斯分布的表达相同,区别在于协方差不同,相关多元正态分布的协方差值表示为:
高斯分布对于x的依赖在于二次型:
这个二次型被叫做µ和x之 间 的 马 ⽒ 距 离 (Mahalanobis distance)。 当Σ是单位矩阵时,就变成了欧式距离。
高斯分布的几何意义:
理解多元高斯分布_anshuai_aw1的博客-CSDN博客_多元高斯分布
高斯过程:
是一个概率统计学上的概念,更确切的说应该是随机过程(Stochastic process)中一个特殊例子。先看看wiki上的定义:
在概率论和统计学中,高斯过程(英语:Gaussian process)是观测值出现在一个连续域(例如时间或空间)的统计模型。在高斯过程中,连续输入空间中每个点都是与一个正态分布的随机变量相关联。此外,这些随机变量的每个有限集合都有一个多元正态分布。高斯过程的分布是所有那些(无限多个)随机变量的联合分布,正因如此,它是连续域(例如时间或空间)的分布。
什么是高斯过程?简单的说,就是一系列关于连续域(时间或空间)的随机变量的联合,而且针对每一个时间或是空间点上的随机变量都是服从高斯分布的。
直观的来解释一下这个概念:
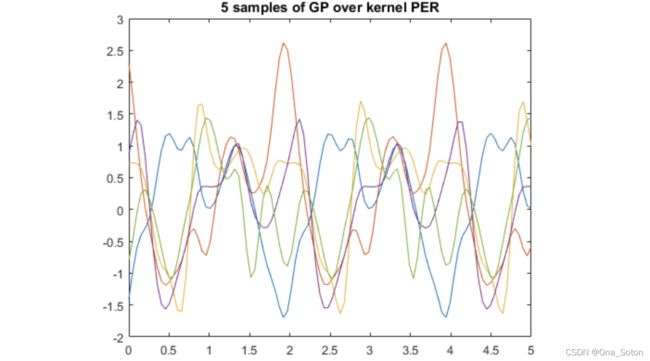 这个一共有5条不同颜色的线,每一条曲线代表了一个GP的样本(这里的kernel是GP的一个重要概念,之后会详细介绍,现在先知道有这个东西就好)。首先我们来看看其中的那个橘黄色的线,对应x轴上找一个点,比如x=2大概对应的的y轴约为2.6左右。可是这真的是一个确定点么?不,它所代表的是对应x=2时的一个随机变量X_{x=2}"正好"出现的点罢了,本质上对应x=2的是一个随机变量而不是一个确定的点。另外对应于任一时刻的随机变量还需要服从一个确定的高斯分布(并不是说所有时刻对应的随机变量需要服从同一个高斯,只是服从的高斯分布的具体参数只跟时刻有关)。除此之外,若是GP的样本,还需要满足的是,任意个点(对应不同时刻的随机变量)联合需要服从多元高斯分布。因此GP的分布就是对于时间域上所有随机变量的联合分布。
这个一共有5条不同颜色的线,每一条曲线代表了一个GP的样本(这里的kernel是GP的一个重要概念,之后会详细介绍,现在先知道有这个东西就好)。首先我们来看看其中的那个橘黄色的线,对应x轴上找一个点,比如x=2大概对应的的y轴约为2.6左右。可是这真的是一个确定点么?不,它所代表的是对应x=2时的一个随机变量X_{x=2}"正好"出现的点罢了,本质上对应x=2的是一个随机变量而不是一个确定的点。另外对应于任一时刻的随机变量还需要服从一个确定的高斯分布(并不是说所有时刻对应的随机变量需要服从同一个高斯,只是服从的高斯分布的具体参数只跟时刻有关)。除此之外,若是GP的样本,还需要满足的是,任意个点(对应不同时刻的随机变量)联合需要服从多元高斯分布。因此GP的分布就是对于时间域上所有随机变量的联合分布。
这不是巧合,而是另有深意,前一个规律是由之前我们提到的一个词语kernel function(核函数),或者covariance function(协方差函数)所决定的,后一个是有mean function所决定的。回头想想,我们刚才说的GP还需要满足什么?对,任意个点(对应不同时刻的随机变量)联合需要服从多元高斯分布!既然是满足多元高斯分布,那么必定需要一个确定的mean和确定的covariance 吧。反过来说,若是给定一个mean和covariance,那么自然不同时刻的随机变量的出现的整体位置和相关情况也就被限定住啦!
因此,一个GP可以被mean和covariance function共同唯一决定!其实这一点应该不难理解吧,因为我们知道一个高斯分布可以被mean和variance共同唯一决定,一个多元高斯分布可以对mean vector和covariance matrix共同唯一决定。当然这个所谓的唯一是指的是表达形式,而不是样本唯一,比如上面的图片就是来自同一个GP的不同样本。
那么整体来说,mean和covariance function分别在画出来的样本中扮演着什么样的角色呢?
正如之前描述的,事实上,mean function决定的样本出现的整体位置,即基准线,若是0的话就是在y=0就是基准线。当然这也是常用的的mean function,其中原因就是它强调于刻画出现样本的整体的位置。另一个原因是在之后我们要说的GP在机器学习中的应用中,一般数据需要进行预处理,而归零中心常常是必须做的。不过,除了0以外,一些线性的mean function也是可以被考虑的。
至于covariance function么,这个才是之后在machine learning的应用中被广为探讨的部分,因而就被称为了核函数kernel,原因就是它捕捉了不同输入点之间的关系,并且反映在了之后样本的位置上。这样的话,就可以做到,利用点与点之间关系,以从输入的训练数据预测未知点的值。
高斯分布与高斯过程:推广与拓展
我们从高斯分布开始,到多元(multvariate)高斯分布,再到矩阵(matrix-variate)高斯分布。这一步一步,的的确确的在拓展,但是这样的扩展还是停留在同一个量,一个随机变量,一个随机向量,一个随机矩阵,这样的提升就好像下面的这个
而从高斯分布到高斯过程,就像手里抓着大把满足高斯分布的随机变量,而这些随机变量是按照时间或者空间这种连续性变量排列的,本质上它是一族随机变量的整体。
举个并不太恰当的例子,倘若你人生的每一个时刻看做一个随机变量,且都是满足高斯分布,那么你的人生就可以看做一个高斯过程,既有很多确定的东西,确定的是mean和kernel,如你的人生中你起点决定的你人生的大致范围,又有极大地不确定性,本质还是随机变量的整体,就像你可以凭借自身的努力改变很多东西,这就是属于你的高斯过程。
高斯混合模型:
高斯混合模型就是将多个高斯分布通过线性组合的方式加在一起(可以理解为多个高斯分布函数的线性组合,理论上高斯混合模型是可以拟合任意类型的分布,另外需要注意的是,通过查阅sklearn的GMM的代码可以知道,面对多维度的数据的情况下,GMM使用的是相关多元高斯分布)
其表达式:
【总结一元和多元高斯】
一元高斯:
使用特征的均值和方差来描述这个单元的高斯分布。
多元独立(相关)高斯:
使用所有特征的均值向量和协方差矩阵来描述多元高斯分布。多元独立高斯和多元相关高斯区别在于协方差矩阵非对角线元素是否为0。
高斯过程:
随机变量(每个时刻可以是一元高斯,可以是多元高斯)是按照时间或者空间这种连续性变量排列的,本质上它是一族随机变量的整体。