时间序列分析——基于R

本文借鉴了王燕的时间序列分析

一、数据的录入

1.简单数据的录入

当数据量较少时，可以直接手打录入

price <- c(101,82,66,35,31,7)
data <- ts(price,start=c(2005,1),frequency = 12)
data

语句说明:
第一句命令是调用c函数.以行输入的方式将6个时序数据依次赋值给了 price 这个变量,price以向量的方式存储这6个数据.
第二句命令是指定price为时间序列变量. 而且序列名为data, start选项 指定序列的起始读入时间，本例中指定序列从2015年1月开始读入 frequency选项指 定序列每年读入的数据频率.本例中指定读入频率为每年12个,也就是说该序列为月度数据.以此类推、读入半年度数据.即frequcncy=2:读入季度数据.即frequency=4: 读入星期数据，即frequency=52;读入日数据.即frequency=365.
第三句命令是查看时间序列data的情况.这条命令输入之后，在对话界面会立刻 出现时间序列data的具体信息.其中行标识是年份，列标识是月份，对应的G个月度 的序列值非常清晰地呈现出来.

2.外部数据导入

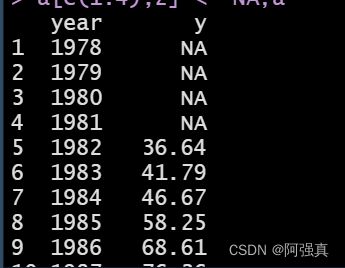
如图是1978年到2016年某地的人均可支配收入，试将其导入，文件名为ts

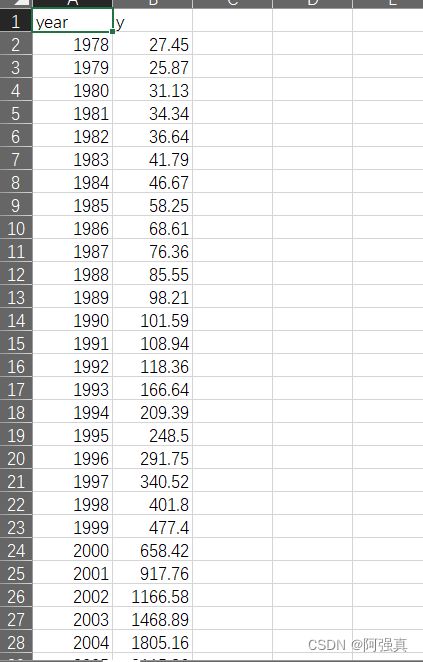
a <- read.csv("ts.csv",header = T);a

这样就导入了

1.对y做对数变换

log(a$y)

2.筛选数据

筛选y中大于1000的数据
使用subset函数可以得到原数据文件的子集.釆用下面的命令我们就能得到一个子集z,原数据文件中的变量y小于1000的数据将被剔除

z <- subset(a,y>1000);z

3.线条插值与样本插值法解决缺失值

如图所示，1978—1981的y为空值，这个时候就需要插值

install.packages("zoo")
library(zoo)
y1 <- na.spline(a);y1#样本插值
y2 <- na.approx(a$y);y2#线性插值

线性插值只需要选中y就好，不要选中整体数据

3.数据的导出

将y取对数后，替换原有数据并导出

ynew <- log(a$y)
year <- a$year
data <- data.frame(year,ynew);data
write.csv(data,file="E:/data.csv")

二、时间序列图的绘制

还是以数据a为例

library(tidyverse)
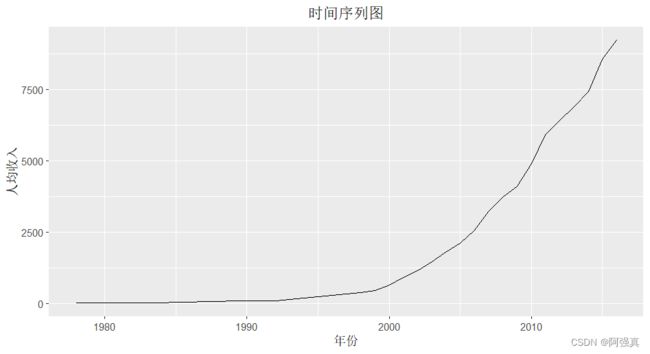
ggplot(a,aes(year,y))+geom_line(lty=1)+
  geom_point(shape=20)+
  scale_x_continuous(breaks = seq(1978,2016,5))#设置x轴的间距
  labs(title='时间序列图',x="年份",y="人均收入")+#添加标题
  theme(plot.title = element_text(hjust=0.5))#标题居中

可以看出：明显增长趋势

三、平稳性的判断

1.时间序列图

通过该图可以看出，此数据有明显的增长趋势，故一定不是平稳序列

2.自相关图检验

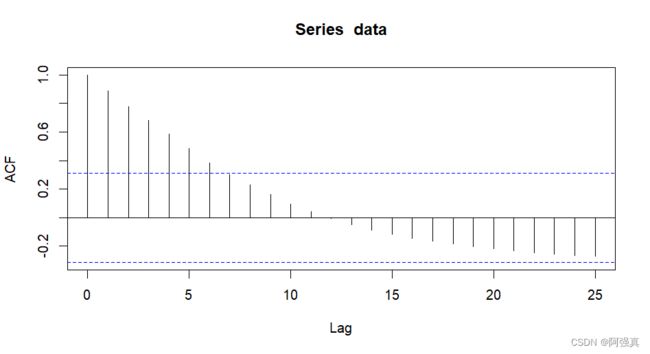
• 绘制1978—2016年的平均人均收入序列自相关

data <- ts(a$y,start=1978);data
acf(data,lag=25)

可以看出自相关系数慢慢的由正变负，从而此数据非平稳

3.纯随机性检验（白噪声检验）

• 随机产生1000个服从标准正态分布的白噪高序列观察值，并绘制时序图和样本自相关图

white_noise <- rnorm(1000)%>%ts()%>%plot()

white_noise <- rnorm(1000)%>%ts()%>%acf()

R语言中使用Box.test函数进行纯随机性检验(白噪声检验)，该函数的命令格式为

white_noise <- rnorm(1000)%>%ts()
Box.test(white_noise,lag=6)

由于P值显著大于显著性水平Q,所以该序列不能拒绝纯随机的原假设.换言之, 我们可以认为该序列的波动没有任何统计规律可循，因而可以停止对该序列的统计分析。

三、平稳时间序列分析

1.AR模型平稳性判别

要拟合一个平稳序列的发展，用来拟合的模型显然也应该是平稳的.AR模型是 常用的平稳序列的拟合模型之-,但并非所有的AR模型都是平稳的.
R提供了多种序列拟合函数、每种函数各"利弊.我们介绍两种最常用的序列拟合方法.

1. arinia.sini 函数拟合
   arinia.sim函数是一个便捷的序列拟合函数.它可以拟合平稳AR序列、MA序列、 平稳ARMA序列和第5章要介绍的ARTMA序列.它的命令格式为：

arima.sim(n, list(ar=, ma=,order=),sd=)

式中：
-n:拟合序列长度.
-list:指定具体的模型参数.其中：
(1) 拟合平稳AR(p）模型，要给出自回归系数.如果指定拟合的AR模型为非平稳模型，系 统
(2) 拟合MA(q)模型，要给出移动平均系教.
(3) 拟合平稳ARMA(p, q)模型，需要同时给出自回归系数和移动平均系数.如果指定拟合 的ARMA模型为韭平稳模％ 系统会报错.
(4) 拟合ARIMA(p,d,g)模型(第5章介绍)，除了需要给出自回归系数和移动平均系#攵， 还需要增加order选项,order=c (p, d, q)#其中，p为目回归阶数;d为差分阶数m 为移动平均吮教.
-sd:指定序列的标准差，不特殊指定，系统默认sd=l.
2. filter函数拟合
filter函数可以直接拟合AR序列(无论是否平稳)和MA序列.filter函数的命令 格式为：

filter(e, filter-, method= ,circular =)

式中：
-e:随机波动序列的变量名.
-filter:指定模型系数.其中：

考察如下两个AR模型的平稳性
$$\left(1\right)x_t=0.8x_{t-1}+{\epsilon }_t\left(2\right)x_t=x_{t-1}+0.5x_{t-2}+{\epsilon }_t$$
首先用不同的方法拟合这两个序列的序列值，并绘制时序图或者自相关图
因为我们是用ggplot2绘图，所以代码多一点

1.时序图

library(ggthemes)
 x1 <- arima.sim(n=100,list(ar=0.8)) %>% data.frame();x1
colnames(x1) <- "y";x1
x2 <- c(1:100)
x3<- data.frame(x1,x2);x3
ggplot(x3,aes(x2,y))+geom_line()+
  scale_x_continuous(breaks=seq(0,100,5))+
  labs(title="时间序列图")+
  theme_solarized()+
  theme(plot.title = element_text(hjust=0.5))

可以看出第一个是平稳的

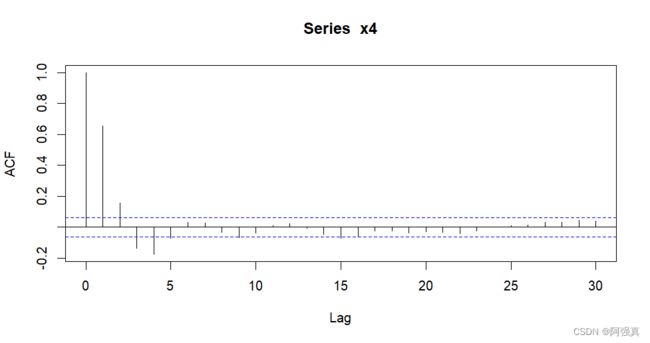
2.相关图

x4 <- arima.sim(n=1000,list(ar=c(1,-0.5)));x4
acf(x4)

即是平稳

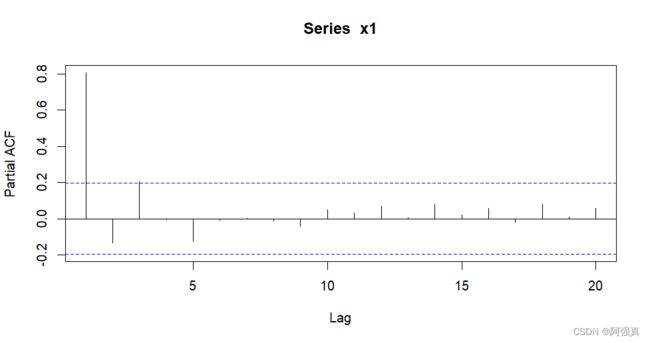
3.偏自相关图

以$\left(1\right)x_t=0.8x_{t-1}+{\epsilon }_t$为例：

x1 <- arima.sim(n=100,list(ar=0.8))
pacf(x1)

2.MA模型

*绘制下例MA模型的样本自相关图，直接考察MA模型自相关系数截尾的特性

$$\left(1\right)x_t={\epsilon }_t-2{\epsilon }_{t-1}\left(2\right)x_t={\epsilon }_t-\frac{4}{5}{\epsilon }_{t-1}+\frac{16}{25}{\epsilon }_{t-2}$$
假定{${\epsilon }_t$}为标准正态白噪声序列

par(mfrow=c(1,2))
x1 <- arima.sim(n=1000,list(ma=-2))
acf(x1)
x2 <- arima.sim(n=1000,list(ma=c(-4/5,16/25)))
acf(x2)

3.ARMA模型

4.平稳序列建模

• 根据1950—1990某地的平均人口收入进行时间序列分析

data <- read.csv("data1.csv") %>%  ts(start = 1950)
Box.test(data)
acf(data)
pacf(data)

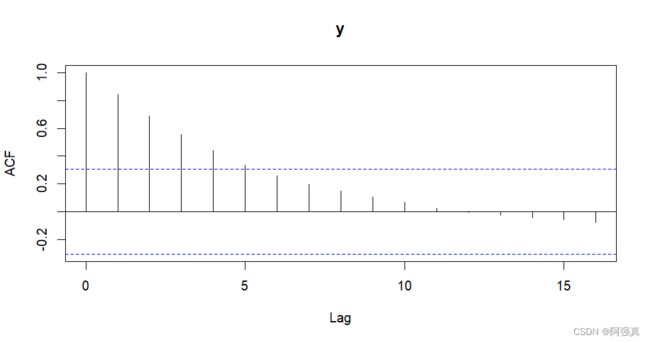
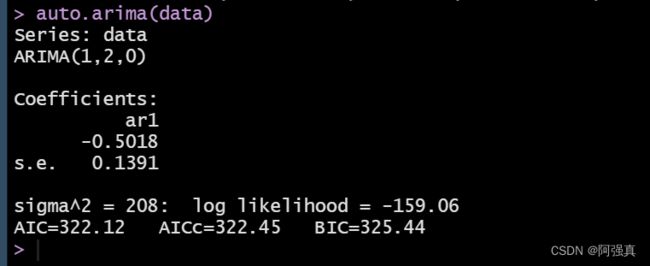
根据上面两幅图可以确定为ARMA(5,1)模型，如果你看不懂这两幅图，那么可以用auto.arima函数自动定阶，首先下载zoo和forecast程序包，并用library 调用这两个程序包.auto.arima函数的命令格式如下：

auto.arima(x, max.p=5, max.q= ）

式中：-x:需要定阶的序列名

• max.p:自相关系数最高阶数，不特殊指定的话，系统默认值为5.
• max.q.移动平均系数最高阶数，不特殊的话默认为5**

install.packages("zoo")
install.packages("forecast")
library(zoo)
library(forecast)  
auto.arima(data)
  

即此模型为ARMA（1,2）模型