学习沐神课程 自用深度学习笔记05 线性回归&基础优化算法

线性回归&基础优化算法

线性回归

导入:

美国买房 价格的影响因素: 卧室个数 卫生间个数 房屋大小 据此给出一个价格

影响因素记为关键因素 成交价记为y 权重为w 偏差为b
$$关键因素:x_1,x_2,x_3$$

$$y=w_1{x}_1+w_2{x}_2+w_3{x}_3+b$$

引入线性模型

$$给定n维输入\mathbf{x}=[x_1,x_2,\dots ,x_n{]}^T$$

线性模型有一个n维权重和一个标量偏差
$$\mathbf{w}=[w_1,w_2,\dots ,w_n{]}^T,b$$
输出的是y即加权和
$$y=w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n+b$$

$$如果用向量来表示的话是y=<\mathbf{w},\mathbf{x}>+b$$

线性模型可以看作是单层的神经网络 即仅有一层输入层 箭头代表权重

衡量预估质量

用于衡量偏差 比较典型的是平方损失
$$假设y为真实值,\hat{y}是估计值,我们比较l(y,\hat{y})=\frac{1}{2}(y-\hat{y}{)}^2$$

训练数据

​ 收集一些数据点决定参数值，在此例子中我们寻找过去六个月卖的房子，训练数据通常越多越好，在数量不足时会有一些算法进行处理

在这里我们设有n个样本，记
$$\mathbf{X}=[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_{\mathbf{n}}{]}^T\mathbf{y}=[y_1,y_2,\dots ,y_n{]}^T$$

参数学习

1. 训练损失
   $$l(\mathbf{X},\mathbf{y},\mathbf{w},b)=\frac{1}{2n}\sum _{i=1}^n(y_i-<{\mathbf{x}}_i,\mathbf{w}>-b{)}^2=\frac{1}{2n}||\mathbf{y}-\mathbf{X}\mathbf{w}-b|{|}^2$$
   这是我们要训练的函数，即我们会将参数X、y代入得到关于w、b的函数

2. 最小化损失
   $${\mathbf{w}}^{\ast },b^{\ast }=arg\underset{\mathbf{w},b}{\min }l(\mathbf{X},\mathbf{y},\mathbf{w},b)$$

3. 显示解

   ​ 值得注意的是，线性模型是有显示解的，也是课程里唯一有显示解、最优解的模型。

   ​ 我们可以将偏差加入权重向量，具体做法是在输入矩阵末尾加入全1行向量，在权重向量末尾添加b，道理比较浅显。

   ​ 在此前提下，损失函数对权重向量求导，由于损失函数是个凸函数，最优解在导函数为0是取得。

基础优化算法

梯度下降

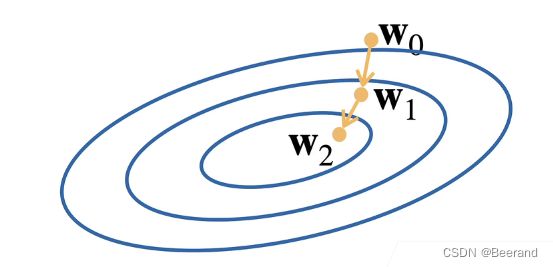
1. 挑选初始值 $w_0 $

2. 对t迭代
   $${\mathbf{w}}_t={\mathbf{w}}_{t-1}-\eta \frac{\delta l}{\delta {\mathbf{w}}_{t-1}}$$

   • 沿梯度方向增加损失函数值 自然沿反方向会减少值
   • 学习率：步长 是一个超参数
     

​ 事实上，每一个黄色箭头相当于迭代一次，沿梯度下降最快的方向前进一个步长。

​ 注意：选择学习率不能太小（计算代价太大，容易陷入局部最优解）

​ 也不能太大（容易发生震荡现象）

小批量随机梯度下降

• 由于在整个训练集上算梯度太贵

• 我们选择随机采样b个样本 $i_1,i_2,\dots ,i_b$ 来近似损失
  $$\frac{1}{b}\sum _{i\in I_b}l({\mathbf{X}}_i,y_i,\mathbf{w})$$

  • b为批量大小，是另一个重要的超参数

小规模随机梯度下降的优点是采用样本近似，在一定程度上会降低内存消耗

需要注意的是批量大小的选择同样要适中，后续会有对其选择的讲解

代码实现(不调包版)

• 导入包

  %matplotlib inline  # 在作图时plot的结果嵌入到notebook里面
  import random  # 随机梯度下降的随机数
  import torch
  from d2l import torch as d2l  # 一些简单的函数
  

• 构造数据集

• $(\mathbf{w}与b可以构造用于检测结果)$我们的任务是使用这个有限样本的数据集来恢复这个模型的参数。 我们将使用低维数据，这样可以很容易地将其可视化。 在下面的代码中，我们生成一个包含1000个样本的数据集， 每个样本包含从标准正态分布中采样的2个特征。 我们的合成数据集是一个矩阵∈ℝ^1000×2。

  $此处\mathbf{w}=[2,-3.4{]}^T,b=4.2$

$$\mathbf{y}=\mathbf{X}\mathbf{w}+b+ϵ$$

• def synthetic_data(w, b, num_examples):  #@save
      """
      生成y=Xw+b+噪声
      此函数相当于一个生成数据集与标签的方法
      用已知的权重与偏差生成一个数据集与标签(注意加了噪音),用此数据集去训练新模型的权重,比较权重与设置的原权重的差距
      """
      # normal(a,b,c)方法:产生均值为a,方差为b的正态随机数,形状由c指定
      X = torch.normal(0, 1, (num_examples, len(w)))
      y = torch.matmul(X, w) + b  # matmul()方法:矩阵相乘
      y += torch.normal(0, 0.01, y.shape)  # 产生噪音
      # 将y变为列向量返回 -1是通配符,表示行数由torch自动推断
      return X, y.reshape((-1, 1))  
  

• true_w = torch.tensor([2, -3.4])  # 设置真实权重
  true_b = 4.2  # 设置偏差
  features, labels = synthetic_data(true_w, true_b, 1000)  # 得到数据集与标签
  print('features:', features[0],'\nlabel:', labels[0])  
  # result:features: tensor([-1.6092, -0.5917]) 输出了一个数据样本观察
  #        label: tensor([2.9942])
  

• d2l.set_figsize()  # 设置画布大小并展示
  d2l.plt.scatter(features[:, (1)].numpy(), labels.detach().numpy(), 1);  # 以第二个特征与标签为参数画平面图 要注意把tensor转化成numpy数组,不加detach可能会转化失败,detach()方法前面讲过是把其转换为纯数值的形式,忽略梯度等其他参数 scatter()方法最后一个参数是散点直径大小
  

• 读取数据集

• 定义一个data_iter函数， 该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量

• def data_iter(batch_size, features, labels):
      # len()返回第一维的长度,在此即为样本个数
      num_examples = len(features)  
      # 相当于将样本个数的下标储存在indices里
      indices = list(range(num_examples))
      # 这些样本是随机读取的，没有特定的顺序,shuffle()为打乱顺序
      random.shuffle(indices)
      for i in range(0, num_examples, batch_size):
          # 除最后一次外, 每次返回batch_size大小的数据样本
          batch_indices = torch.tensor(
              indices[i: min(i + batch_size, num_examples)])
          # yield为迭代器, tensor可以作为tensor的下标
          # 相当于每次返回一个值并记住返回位置,下次循环从当前位置继续
          yield features[batch_indices], labels[batch_indices]
  

• 通常，我们利用GPU并行运算的优势，处理合理大小的“小批量”。 每个样本都可以并行地进行模型计算，且每个样本损失函数的梯度也可以被并行计算。 GPU可以在处理几百个样本时，所花费的时间不比处理一个样本时多太多。

  我们直观感受一下小批量运算：读取第一个小批量数据样本并打印。 每个批量的特征维度显示批量大小和输入特征数。 同样的，批量的标签形状与batch_size相等。

• batch_size = 10
  
  for X, y in data_iter(batch_size, features, labels):
      print(X, '\n', y)
      break
  

• result:

• tensor([[-2.1381, -0.6025],
          [ 0.6795, -0.3631],
          [ 0.7773, -2.9904],
          [-2.5818, -0.3094],
          [ 0.7813,  0.9239],
          [-1.3962,  0.1726],
          [-1.7048, -0.1011],
          [ 0.5355, -0.1169],
          [ 1.7521, -1.9358],
          [-0.8637, -0.1053]]) 
   tensor([[ 1.9699],
          [ 6.7943],
          [15.9225],
          [ 0.1035],
          [ 2.6211],
          [ 0.8109],
          [ 1.1404],
          [ 5.6749],
          [14.2923],
          [ 2.8181]])
  

• 当我们运行迭代时，我们会连续地获得不同的小批量，直至遍历完整个数据集。 上面实现的迭代对于教学来说很好，但它的执行效率很低，可能会在实际问题上陷入麻烦。 例如，它要求我们将所有数据加载到内存中，并执行大量的随机内存访问。 在深度学习框架中实现的内置迭代器效率要高得多， 它可以处理存储在文件中的数据和数据流提供的数据。

• 初始化模型参数

• # 随机产生w与b作为初始值
  w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
  b = torch.zeros(1, requires_grad=True)
  

• def linreg(X, w, b):  #@save 保存在了d2l包中,可以直接调用
      """线性回归模型"""
      return torch.matmul(X, w) + b
  

• def squared_loss(y_hat, y):  #@save  同样的
      """均方损失的简单实现"""
      # 注意此函数没有对样本求均值
      return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
  

• def sgd(params, lr, batch_size):  #@save
      """小批量随机梯度下降"""
      # with方法:执行函数__enter__ 结束之后执行__exit__
      # torch.no_grad()方法,在此区域内产生的张量grad属性均为False 即使生成它的张量为True
      with torch.no_grad():
          for param in params:
              param -= lr * param.grad / batch_size  # 梯度下降算法 在此取了平均值
              param.grad.zero_()
  

• 训练

• lr = 0.03  # 学习率
  num_epochs = 3  # 迭代周期数
  net = linreg  # 模型 为方便更换
  loss = squared_loss  # 损失函数
  

• for epoch in range(num_epochs):
      for X, y in data_iter(batch_size, features, labels):
          l = loss(net(X, w, b), y)  # X和y的小批量损失
          # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起
          # 并以此计算关于[w,b]的梯度
          l.sum().backward()  # backword()方法会更新梯度,注意到损失函数的未知量是权重与偏差
          sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
      with torch.no_grad():
          train_l = loss(net(features, w, b), labels) # 得到当前迭代周期的损失值
          print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
  

代码实现(调包版)

• 导入包

• import numpy as np
  import torch
  from torch.utils import data  # PyTorch中提供的进行数据处理的组件
  from d2l import torch as d2l
  

• 生成数据集

• true_w = torch.tensor([2, -3.4])
  true_b = 4.2
  features, labels = d2l.synthetic_data(true_w, true_b, 1000)  # 封装的生成数据集的函数 (不调包版实现了该函数)
  

• 读取数据集

• def load_array(data_arrays, batch_size, is_train=True):  #@save
      """构造一个PyTorch数据迭代器"""
      dataset = data.TensorDataset(*data_arrays)
      # is_train是一个bool值,表示是否希望打乱顺序读取 默认为True
      return data.DataLoader(dataset, batch_size, shuffle=is_train)  # PyTorch中自带的数据迭代器,类似于前述的yield
  

• batch_size = 10
  data_iter = load_array((features, labels), batch_size)  # data_iter即为一个迭代器 可以作为for _ in data_iter使用
  

• next(迭代器)函数可以从迭代器中读取一个数据并记录位置,下次next时输出当前的下一个数据

• 定义模型

• # nn是神经网络的缩写,PyTorch的nn中存储了大量的神经网络模型
  from torch import nn  
  
  # Linear接受两个param,一个是输入规模,一个是输出规模
  net = nn.Sequential(nn.Linear(2, 1))  # Sequential是一个容器,里面可以存储一张完整的神经网络 在此只有一层全连接层
  

• Sequential的解释: Sequential类将多个层串联在一起。 当给定输入数据时，Sequential实例将数据传入到第一层， 然后将第一层的输出作为第二层的输入，以此类推。 在下面的例子中，我们的模型只包含一个层，因此实际上不需要Sequential。 但是由于以后几乎所有的模型都是多层的，在这里使用Sequential会让你熟悉“标准的流水线”。

• 初始化模型参数

  net[0].weight.data.normal_(0, 0.01)  # weight.data用于访问权重的数据 normal_方法用于填充数据(正态分布随机)
  net[0].bias.data.fill_(0)  # 同上 bias为偏置
  

• 定义损失函数

• loss = nn.MSELoss()  # MSELoss方法又称为2-范数,默认返回所有样本损失的平均值
  

• 定义优化方法

• # optimize(优化) optim内存储了众多优化方法 SGD即前述实现过的随机梯度下降算法,可以调用net.parameters()方法获取需要优化的参数,SGD算法只需指定一个超参数学习率
  trainer = torch.optim.SGD(net.parameters(), lr=0.03) 
  

• 训练

• num_epochs = 3  # 迭代周期数
  for epoch in range(num_epochs):
      for X, y in data_iter:  # data_iter:迭代器
          l = loss(net(X) ,y)  # 生成预测并通过计算损失l(前向传播)
          trainer.zero_grad()  # 清空优化器trainer的梯度
          l.backward()  # 反向传播更新梯度
          trainer.step()  # 优化器step()方法更新参数
      l = loss(net(features), labels)
      print(f'epoch {epoch + 1}, loss {l:f}')