HotSpot-多维属性的kpi异常定位(根因分析)
最近公司有这方面的需求,所以,就找一些论文和资料来了解一下在异常检测基础之上,如何做到对异常或者故障的根因分析。
有两种根因分析的需要,一种就是单指标异常检测,就是指标就是一维的这种,如果这种指标发生异常,直接就能够锁定到相关时间,位置,如果这种做异常检测,自然就需要升维,就是比如说,同时针对几个指标来进行,用窗口划分,然后看看同一时间段,都有哪些指标发生异常,然后这些窗口内的数据就组成原始处理数据,后续再处理。
一种就是这篇论文讲的,在多维kpi上进行根因定位,如果某一个多维kpi发生异常,你怎么知道具体是哪些属性发生了变化,是哪些属性导致了最终的异常的发生了?
这也就是这篇文章要解决的问题。
HotSpot: Anomaly Localization for Additive KPIs With Multi-Dimensional Attributes
这篇文章是裴丹老师他们发表的一篇文章,时间在2018年。
两个挑战
1、不同组合的多维指标相互依赖,对于定位多维指标异常是在哪一个聚合层次导致了多维指标发生改变是困难的;
2、当多维指标的纬度大到一定程度,会有成千上万的不同组合是可能导致异常发生的原因,其搜索空间巨大,找到导致异常发生的组合也是困难的;
整体思路
针对以上两个挑战,该论文提出了两个主要的解决办法,
1、基于异常传播的波动影响力计算可能性分值,来解决第一类问题;
2、用蒙特卡罗搜索树算法以及分级(hierarchical)剪枝策略来解决第二类问题;
效果
百分之九十五类型的根因分析,F值能够超过0.9,运维人员的体验显示,该算法能够把根因定位时间从人工1个小时降低到20s。
主要内容
基本概念介绍
pv -page view
| 术语 | 定义 | 标记 | 例子 |
|---|---|---|---|
| 属性 | 每一个pv记录的信息类别 | ---- | 省份(P),ISP(I),数据中心(D),频道(C) |
| 属性值 | 每一个属性可能的值 | ---- | 比如对于省份(北京,上海,广东) |
| 元素 | 对于每一个属性的不同值组合向量 | e=(p,i,d,c) | 例如(北京,* ,* ,*) |
| PV 值 | 一个元素的访问数量 | v(ei) | v(beijing,* ,* ,*) |
| 预测值 | 用历史值预测一个元素未来数值 | f(ei) | f(beijing, * ,* ,* ) |
| 数据立方体 | 多维数据的数据结构 | n-d 立方体 | 一个4维数据立方体(p,i,d,c) |
| 立方体 | 所给纬度的子集 | Bi | 比如(Bi,Bp,j,Bp,i,d,w) |
| 可能性分值 | 用来衡量一组元素是根本原因的可能性 | ps | ps(S),S={(beijing, * , * , * ),(* ,mobile, * , *)} |
PV 记录
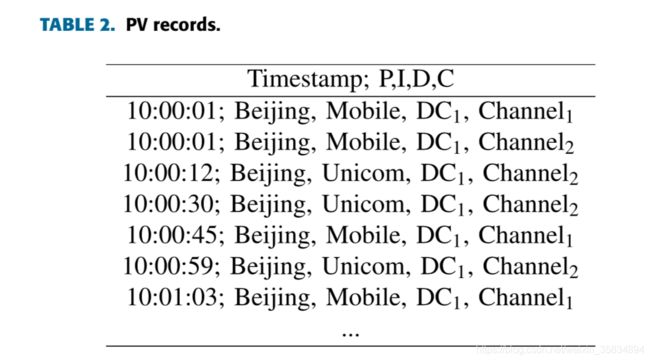
通过对这些日志记录的统计,比如说,按照每分钟的统计,我们可以得到下边的统计结果:

通过对一段时间内的如上日志统计,我们会得到下边的数据结构
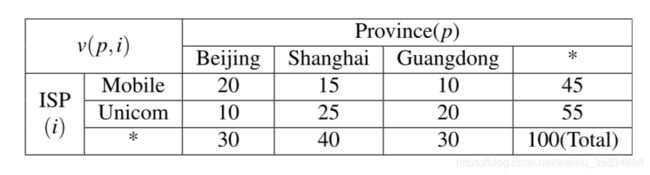
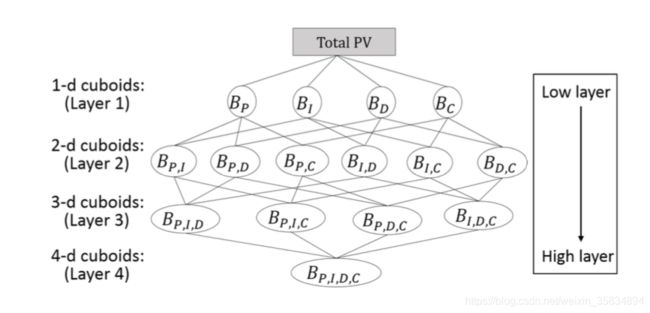
针对四维的PV数据立方体,我们看一下,它可以表示为两个三维立体
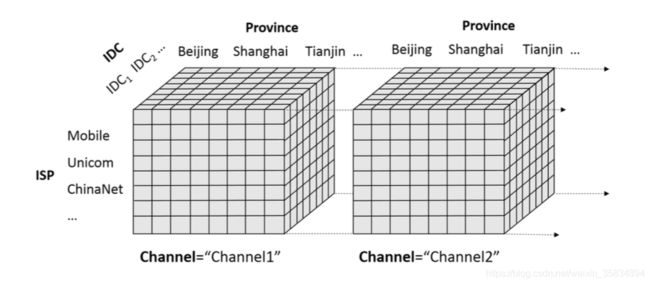
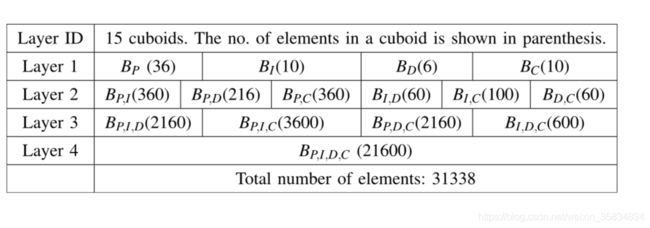
对于我们目前一直在谈论的page views的子集组合以及其层次,我们可以分为四个层次
问题再表述
对于多维kpi,异常定位问题,就是找到导致总kpi数值发生异常变化的最有可能的组合子集。
挑战
1、如何衡量一个组合会成为根本原因的方式,这种方式并不容易,
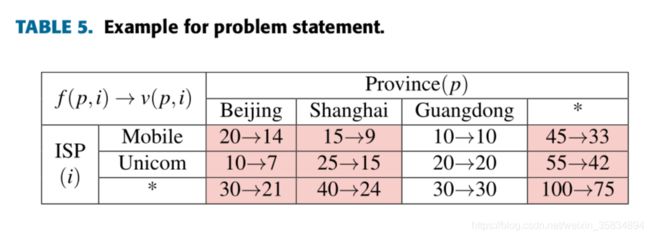
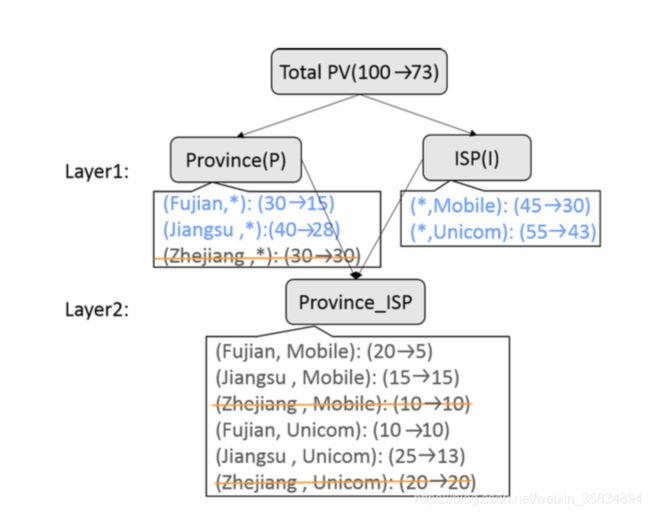
如上面图所示,直觉的会感觉用变化比例,但是这个并不好用。
文中用h(e)来表示一组组合变化
比如h(total)=25
之所以不用变化比例,是因为有的不同组合有可能变化比例相同,难以分清两个,那个可能是根因的可能性大
2、有很多集合需要被比对,
之所以很多集合需要被计算,去比对,因为ps这个指标不具备可分解特性,比如ps({e1,e2})!=ps({e1})+ps({e2})
蒙特卡罗搜索以及分级剪枝
论文作者受到MCTS在alphaGo上的优秀表现启发,所以准备使用这种方法来在搜索空间中进行最可能根因搜索,而分级剪枝则是受到以下直觉启发:
如果父亲组成集合不可能是根因组合,那么说明它的每一个孩子组合都不可能是是根因组合。
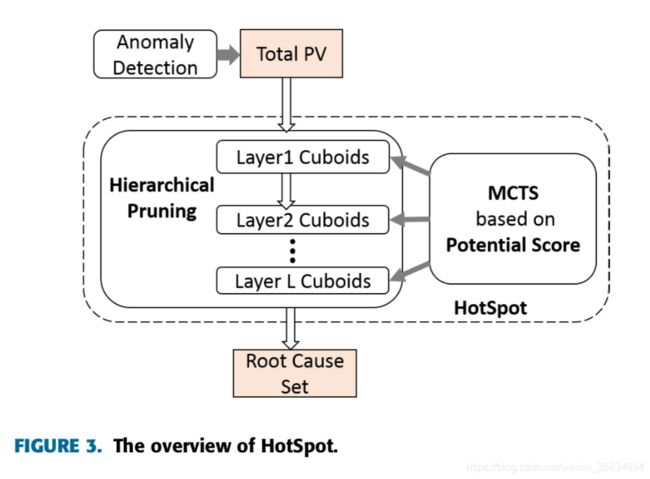
hotspot架构全览
依赖
这种方法依赖异常检测以及预测,虽然有了对于不同组合的统计,但是如果没有相对应的预测值以及检测方法,那就不知道异常是什么,那就无法针对该异常进行根因分析。
三大核心步骤
可能性分数计算
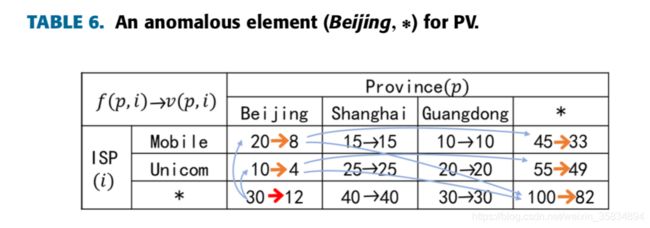
我们可以看到这个整体的变化都是由于(beijing,*)造成的,
v ( x i ′ ) = f ( x i ′ ) − h ( x ) × f ( x i ′ ) f ( x ) , ( f ( x ) ≠ 0 ) v\left(x_{i}^{\prime}\right)=f\left(x_{i}^{\prime}\right)-h(x) \times \frac{f\left(x_{i}^{\prime}\right)}{f(x)},(f(x) \neq 0) v(xi′)=f(xi′)−h(x)×f(x)f(xi′),(f(x)̸=0)
x是一个完整的集合,x‘ 是一个集合中的子集,如果一个组合发生了变化,那么其子集肯定对这个整体的变化有变化贡献,通过以上方式可以计算不同子集的变化贡献。
可能性分数计算
1、假设某个组合是根因
2、新降低的pv数值,
3、比对新降低的pv值与实际的pv值,越相近,是异常的可能性越大
Potential Score = max ( 1 − d ( v ⃗ , a ⃗ ) d ( v ⃗ , f ⃗ ) , 0 ) \text { Potential Score }=\max \left(1-\frac{d(\vec{v}, \vec{a})}{d(\vec{v}, \vec{f})}, 0\right) Potential Score =max(1−d(v,f)d(v,a),0)
可能性分数的范围就是0-1,分数值越高,是根因的可能性越大
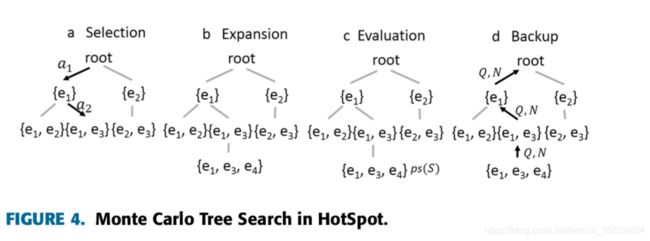
蒙特卡罗搜索
-
选择
先计算每一个组合的可能性分数,然后进行排名,
Q ( s , a ) = max u ∈ { s ′ } ∪ d e s c e n d e n t ( s ′ ) p s ( S ( u ) ) Q(s, a)=\max _{u \in\left\{s^{\prime}\right\} \cup d e s c e n d e n t\left(s^{\prime}\right)} p s(S(u)) Q(s,a)=u∈{s′}∪descendent(s′)maxps(S(u))
a = arg max a ∈ A ( s ) { Q ( s , a ) + C ln N ( s ) N ( s , a ) } a=\underset{a \in A(s)}{\arg \max }\left\{Q(s, a)+C \sqrt{\frac{\ln N(s)}{N(s, a)}}\right\} a=a∈A(s)argmax{Q(s,a)+CN(s,a)lnN(s)}
Q(s, a)执行步骤a的数值,数值越大,执行步骤a的可能性越大 -
扩展
当一个状态s被选择之后,开始进行扩展,增加新的节点S’
S ( s ′ ) = S ( s ) ∪ { e ∗ } S\left(s^{\prime}\right)=S(s) \cup\left\{e^{*}\right\} S(s′)=S(s)∪{e∗}
e ∗ = max e ∈ { e 1 , e 2 , … , e n } − S ( s ) p s ( e ) e^{*}=\max _{e \in\left\{e_{1}, e_{2}, \ldots, e_{n}\right\}}-S(s) p s(e) e∗=e∈{e1,e2,…,en}max−S(s)ps(e)
扩展标准就是选择一个最大的e* 使得余下的组合有最大的ps(S)
- 评估
初始化扩展后新的节点,计算ps,Q,N - 回溯
进行以上四步骤,直到满足以下三个条件之一:
- 一个最好的组合找到了
- 所有可用的节点都被扩展了
- 迭代次数已经超过限制,
分级剪枝
之前我们就说过了这个剪枝策略,其实这个策略确实和apriori 频繁项集的确实很像,
为了降低计算成本,我们看个例子
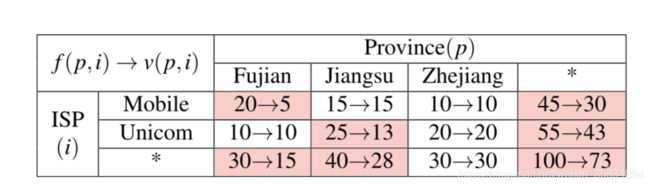
假设在第一层,有两个数据
BSet1.Bp={(Fujiang, ),(Jiangsu, )} ps(BSet1.Bp)=0.5
BSet1,Bi={(,Mobile),(,Unicom)} ps(BSet1,Bi)=0.32
当在我搜索第二层的时候,{(Zhejiang,Unicom)} 就不用再计算了,因为{(Zhejiang, *)} 不在BSet中