漫步微积分二十八——极限思想下的面积计算

上篇文章中讨论的概念给出了计算面积的实际过程。现在我们利用一些实例来测试这个过程是如何工作的。

例1：考虑区间 [0,b] 上的函数 y=f(x)=x 。图像(图1)下面的区域是高和底都为 b 的矩形，所以它的面积明显是b2/2。然而，我们需要去证实我们极限过程给出相同的答案，更重要的是，理解立即过程如何给出答案。

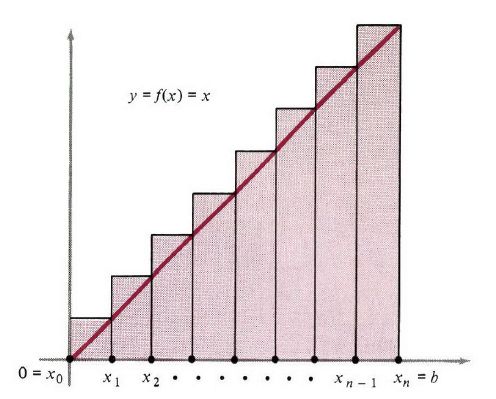
图1

n 是一个正整数，区间[0,b]分割成相等的 n 个子区间，得到n−1个间断点

x1=bn,x2=2bn,…,xn−1=(n−1)bn(1)

矩形的底是 Δxk=b/n ，如果我们用图1那样的上部和，那么矩形的高为

f(x1)=bn,f(x2)=2bn,…,f(xn−1)=(n−1)bn

于是我们有

Sn=(bn)(bn)+(2bn)(bn)+⋯+(nbn)(bn)=b2n2(1+2+⋯+n)

利用之前讲过的求和公式，可以写成

Sn=b2n2⋅n(n+1)2=b22⋅nn⋅n+1n=b22(1+1n)

所以我们得到

area of region=limn→∞Sn=limn→∞b22(1+1n)=b22

这就是开始我们得到的。用定积分的符号表示就是

∫baxdx=b22(2)

在本例中我们选择了相等的子区间及上部和。不代表必须作出这些选择；我们的目的仅仅是为了使计算尽可能容易。

例2：现在考虑区间 [0,b] 上的函数 y=f(x)=x2 ，如图2所示。 n 是一个正整数，区间[0,b]分割成相等的 n 个子区间，长度为Δxk=b/n。我们继续用上部和 Sn ，所以矩形的高度为

f(x1)=(bn)2,f(x2)=(2bn)2,…,f(xn−1)=((n−1)bn)2

从而得到

Sn=(bn)2(bn)+(2bn)2(bn)+⋯+(nbn)2(bn)=b3n3(12+22+⋯+n2)

利用前面文章提到的公式，上式可写为

Sn=b3n3⋅n(n+1)(2n+1)6=b36⋅nn⋅n+1n⋅2n+1n=b3n3(1+1n)(2+1n)

当 n→∞ 时我们得到

area of region=limn→∞Sn=b33

或等价地

∫bax2dx=b33(3)

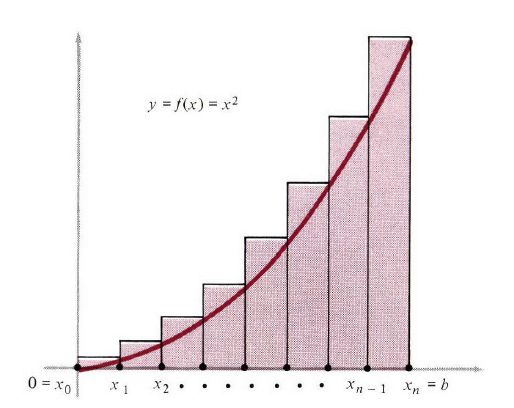
图2

用同样的方式我们可以得到 y=f(x)=x3 的定积分

∫bax3dx=b44(4)

很自然地我们根据(2)(3)(4)可以猜想

∫baxndx=bn+1n+1(5)

它可能对所有正整数 n=1,2,3,… 成立。对于 n=3,4,…,9 的情况，(5)的有效性由意大利数学家Cavalieri在1635年和1647年建立起来，但他费力的几何方法在 n=10 时就很难进行下去。几年以后费马发现了这个美丽的论点，一次就证明了(5)对所有正整数成立。这个论点有点远离我们的这里的主题。

例3：接下来，我们找出余弦曲线 y=cosx 下的面积，从 x=0 开始到 x=b ，其中 0<b≤π/2 (图3)。 n 是一个正整数，将区间[0,b]分割成相等的 n 个子区间，长度为Δxk=b/n。这次我们用下部和 sn 。因为函数是递减的，所以 x¯k 是子区间的右端点。连续矩形的高度是

cosbn,cos2bn,⋯,cosnbn

从而

sn=(cosbn)(bn)+(cos2bn)(bn)+⋯+(cosnbn)(bn)=bn∑k=1ncoskbn

为了计算 n→∞ 时的极限，需要用到下面的计算结果

∑k=1ncoskx=sin12nxcos12(n+1)xsin12x

其中 x=b/n 。从而我们得到

area of region=limn→∞sn=limn→∞bn⋅sin12bcos[(n+1)b2n]sin(b/2n)(6)

为了计算极限，考虑到余弦函数是连续的，可以看出

cos[(n+1)b2n]=cos(1+1n)b2→cosb2asn→∞

接下来，如果选 θ=b/2n ，那么当 n→∞ 时， θ→0 那么

bn⋅1sin(b/2n)=2⋅b/2nsin(b/2n)=2⋅θsinθ→2asn→∞

利用这些事实(6)可写为

area of region=limn→∞sn=2sinb2cosb2=sinb

或者等价地

∫b0cosxdx=sinb

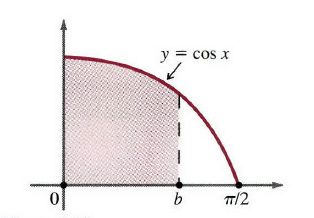
图3