多元线性回归算法预测房价【人工智能】

一、理论知识

一元线性回归是分析只有一个自变量（自变量x和因变量y）线性相关关系的方法。一元线性回归分析的数学模型为：y = a+bx+ε。
使用偏差平方和分别对参数a和参数b求偏导，可以得到线性模型的未知参数a、b的最小二乘估计值，其中，偏差平方和定义为∑(yi-a-bXi)2，a和b的唯一解如图所示。

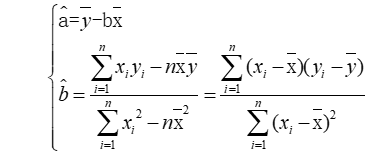
参数的最小二乘估计

为了方便回归效果显著性检验，根据b的估计，引入LXX、LYY、LXY三个数学符号，这三个数学符号定义如图所示。
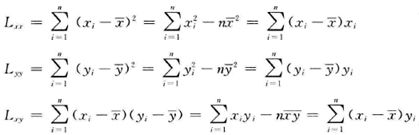LXX、LYY、LXY的数学定义

在现实问题研究中，因变量的变化往往受几个重要因素的影响，此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化，这就是多元回归。也就是说，当多个自变量与因变量之间是线性关系时，所进行的回归分析就是多元性回归。多元线性回归的数学模型为：y=β0+β1X1+β2X2+…++βpXp+ε。使用残差平方和分别对参数βi（i=0,1,…,p）求偏导，可以得到线性模型的未知参数βi（i=0,1,…,p）的估计值，β矩阵的估计值如图2-3所示。

二、Excel多元线性回归

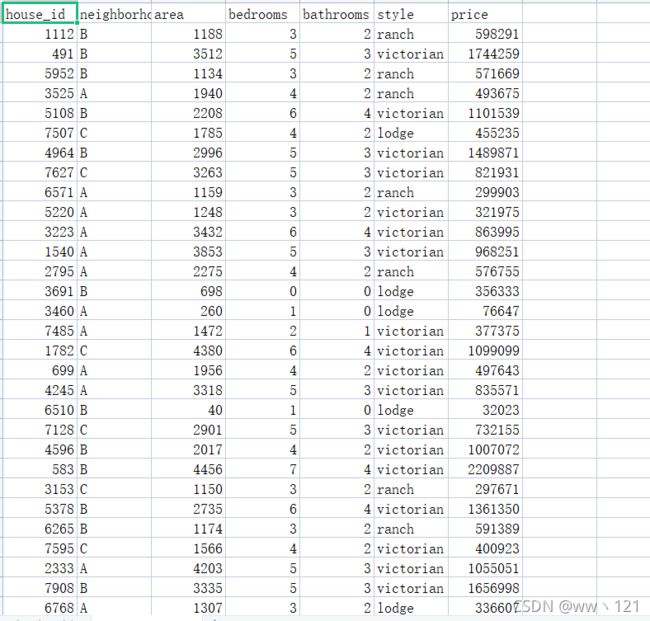
1.数据集

2.数据分析

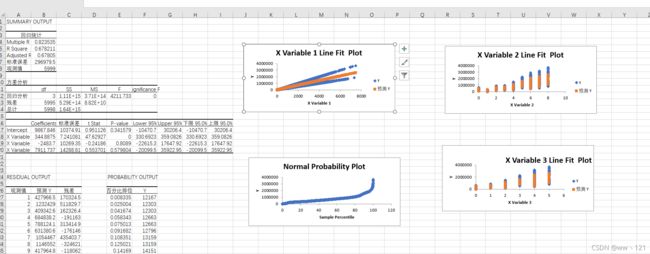
• 在Excel打开house_prices.csv文件，在数据选项中打开数据分析，选择其中的回归。
• 在选择其中的area，bathroom，bedroom作为x，可以得出三相数据和price是正相关。而黄线部分得出了对房价的预测。
  

三、借助Sklearn库实现多元线性回归

1.基础包与数据导入

查看数据基础信息

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt#导入数据
df = pd.read_csv("E:\人工智能\house_prices1.csv")
#读取数据的基础信息
df.info()

2.变量探索

数据处理

# 异常值处理
# ================ 异常值检验函数：iqr & z分数 两种方法 =========================
def outlier_test(data, column, method=None, z=2):
    """ 以某列为依据，使用 上下截断点法 检测异常值(索引) """
    """ 
    full_data: 完整数据
    column: full_data 中的指定行，格式 'x' 带引号
    return 可选; outlier: 异常值数据框 
    upper: 上截断点;  lower: 下截断点
    method：检验异常值的方法（可选, 默认的 None 为上下截断点法），
            选 Z 方法时，Z 默认为 2
    """
    # ================== 上下截断点法检验异常值 ==============================
    if method == None:
        print(f'以 {column} 列为依据，使用 上下截断点法(iqr) 检测异常值...')
        print('=' * 70)
        # 四分位点；这里调用函数会存在异常
        column_iqr = np.quantile(data[column], 0.75) - np.quantile(data[column], 0.25)
        # 1，3 分位数
        (q1, q3) = np.quantile(data[column], 0.25), np.quantile(data[column], 0.75)
        # 计算上下截断点
        upper, lower = (q3 + 1.5 * column_iqr), (q1 - 1.5 * column_iqr)
        # 检测异常值
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        print(f'第一分位数: {q1}, 第三分位数：{q3}, 四分位极差：{column_iqr}')
        print(f"上截断点：{upper}, 下截断点：{lower}")
        return outlier, upper, lower
    # ===================== Z 分数检验异常值 ==========================
    if method == 'z':
        """ 以某列为依据，传入数据与希望分段的 z 分数点，返回异常值索引与所在数据框 """
        """ 
        params
        data: 完整数据
        column: 指定的检测列
        z: Z分位数, 默认为2，根据 z分数-正态曲线表，可知取左右两端的 2%，
           根据您 z 分数的正负设置。也可以任意更改，知道任意顶端百分比的数据集合
        """
        print(f'以 {column} 列为依据，使用 Z 分数法，z 分位数取 {z} 来检测异常值...')
        print('=' * 70)
        # 计算两个 Z 分数的数值点
        mean, std = np.mean(data[column]), np.std(data[column])
        upper, lower = (mean + z * std), (mean - z * std)
        print(f"取 {z} 个 Z分数：大于 {upper} 或小于 {lower} 的即可被视为异常值。")
        print('=' * 70)
        # 检测异常值
        outlier = data[(data[column] <= lower) | (data[column] >= upper)]
        return outlier, upper, lower

调用函数

outlier, upper, lower = outlier_test(data=df, column='price', method='z')
outlier.info(); outlier.sample(5)

删除错误数据

# 这里简单的丢弃即可
df.drop(index=outlier.index, inplace=True)

3.分析数据

定义变量

# 类别变量，又称为名义变量，nominal variables
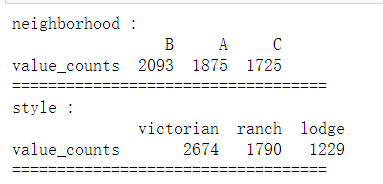
nominal_vars = ['neighborhood', 'style']

for each in nominal_vars:
    print(each, ':')
    print(df[each].agg(['value_counts']).T)
    # 直接 .value_counts().T 无法实现下面的效果
     ## 必须得 agg，而且里面的中括号 [] 也不能少
    print('='*35)
    # 发现各类别的数量也都还可以，为下面的方差分析做准备

热力图查看变量关联性

# 热力图 
def heatmap(data, method='pearson', camp='RdYlGn', figsize=(10 ,8)):
    """
    data: 整份数据
    method：默认为 pearson 系数
    camp：默认为：RdYlGn-红黄蓝；YlGnBu-黄绿蓝；Blues/Greens 也是不错的选择
    figsize: 默认为 10，8
    """
    ## 消除斜对角颜色重复的色块
    #     mask = np.zeros_like(df2.corr())
    #     mask[np.tril_indices_from(mask)] = True
    plt.figure(figsize=figsize, dpi= 80)
    sns.heatmap(data.corr(method=method), \
                xticklabels=data.corr(method=method).columns, \
                yticklabels=data.corr(method=method).columns, cmap=camp, \
                center=0, annot=True)
    # 要想实现只是留下对角线一半的效果，括号内的参数可以加上 mask=mask

调用函数输出结果

# 通过热力图可以看出 area，bedrooms，bathrooms 等变量与房屋价格 price 的关系都还比较强
 ## 所以值得放入模型，但分类变量 style 与 neighborhood 两者与 price 的关系未知
heatmap(data=df, figsize=(6,5))

4.建立线性回归模型

使用最小二乘法建立线性回归模型

from statsmodels.formula.api import ols
#最小二乘法建立线性回归模型
lm = ols('price ~ area + bedrooms + bathrooms', data=df).fit()
lm.summary()

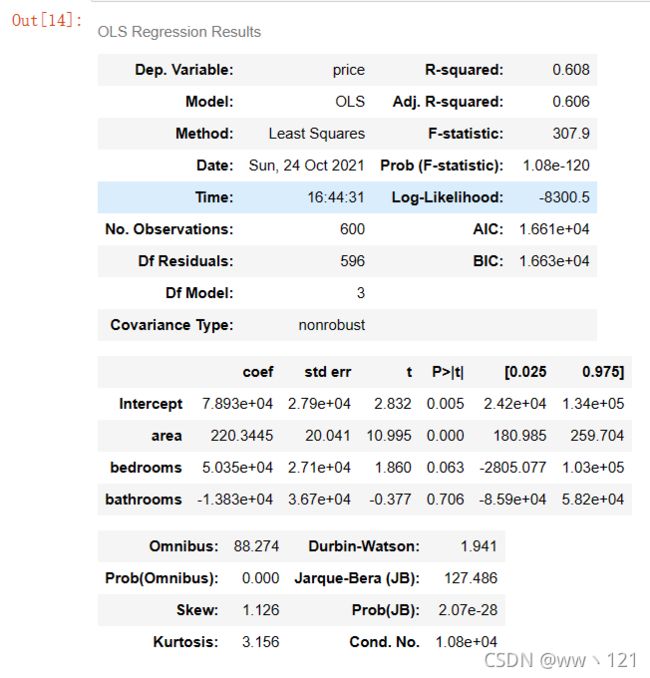模型优化
模型精度较低，这里通过添加虚拟变量与使用方差膨胀因子检测多元共线性的方式来提升模型精度

# 设置虚拟变量
# 以名义变量 neighborhood 街区为例
nominal_data = df['neighborhood']

# 设置虚拟变量
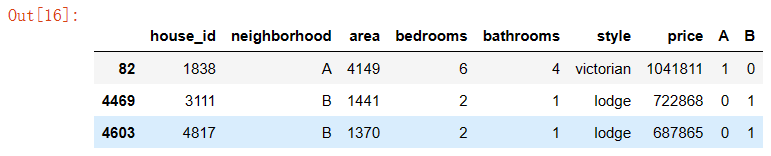
dummies = pd.get_dummies(nominal_data)
dummies.sample()  # pandas 会自动帮你命名

# 每个名义变量生成的虚拟变量中，需要各丢弃一个，这里以丢弃C为例
dummies.drop(columns=['C'], inplace=True)
dummies.sample()

结果与原数据集连接

# 将结果与原数据集拼接
results = pd.concat(objs=[df, dummies], axis='columns')  # 按照列来合并
results.sample(3)
# 对名义变量 style 的处理可自行尝试

lm = ols('price ~ area + bedrooms + bathrooms + A + B', data=results).fit()
lm.summary()

5.Sklearn库建立多元线性回归模型

#导入相关库
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split #这里是引用了交叉验证
from sklearn.linear_model import LinearRegression  #线性回归
from sklearn.linear_model import Lasso, Ridge, LinearRegression as LR
from sklearn.metrics import r2_score, explained_variance_score as EVS, mean_squared_error as MSE
from sklearn.model_selection import train_test_split, cross_val_score
from pandas.core.accessor import register_dataframe_accessor

读入数据

data=pd.read_csv('E:\人工智能\house_prices.csv')
x = data[['neighborhood','area','bedrooms','bathrooms','style']]#自变量
y= data['price']# 因变量

划分训练集等

x_train, x_test, y_train, y_test = train_test_split(
    x, y, test_size=0.3, random_state=1)

模型训练与求解
判断参数

四、参考文献

1.基于多元线性回归的房价预测

2.多元线性回归之预测房价