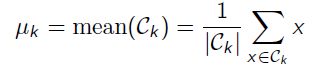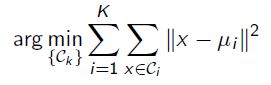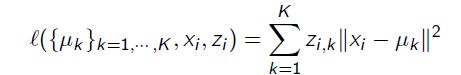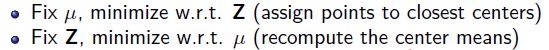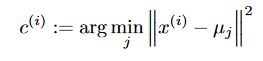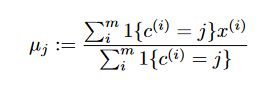山东大学机器学习实验六 K-Means

山东大学机器学习实验6报告

实验学时： 4 实验日期：2021.11.29

实验题目：Experiment 6 : K-Means

实验目的

In this exercise, you will use K-means to compress an image by reducing the
number of colors it contains

使用K-means 通过减少颜色的数量来压缩图像

实验环境

软件环境

​ Windows 10 + Matlab R2020a

​ CPU: Intel® Core™ i5-8300H CPU @ 2.30GHz 2.30 GHz

实验步骤与内容

了解K-Means

K-Means (Lloyd 1957)

1. 更新每个点的Class K: 通过计算每个数据点$X_i$ 到 每个类别中心点${\mu }_k$的距离，来选择某点属于哪个类别

   

2. 更新每个cluster means : 即根据当前这个类别的点，进行求mean操作，来得到中心点

   

3. 当${\mu }_k$或者Loss 不变时，认为迭代完成。

   Loss:

   

Loss Function

${\mu }_k$认为是第K个聚类的质心，$z_{i,k}$认为是$x_i$是否属于$C_k$的一个指示，然后对于每一条数据都会有一个$z_i$，因此定义某个数据$x_i$的$loss$为：

总的$LossFunction:$ 其中$XisN\times D$ 然后 $ZisN\times K且\mu isK\times D$

意思就是X表示所有D维数据，Z表示所有N个数据的聚类类别指示，$\mu$表示K个聚类的D维中心点。K-Means 就是去最小化这个Loss Function

K-Means Objective

​ K-Means 是一个启发式的方法，来解决这个NP-hard问题，并且他是一个Non-Convex problem，存在很多local minima

而算法描述为：

Choosing K

​ 选择聚类的个数也是一个问题。

• ​ 可以通过尝试不同的K值，画对于不同的K下的Loss图，选择elbow point 即可。

• ​ 也可以使用AIC 来求解计算

---

Task Description:

​ Your task is to compute 16 cluster centroids from this image, with each centroid being a vector of length three that holds a set of RGB values.

​ 计算16个聚类，每一个中心点都是一个 $size=3\times 1$的RGB $pixel$像素点 $value$表示RGB的值

​ 鉴于计算 $538\times 538\times 3$的图片的中心点会耗时巨大，因此先在 小图片$(128\times 128\times 3)$训练完之后，应用在大图片上，得到一个只使用16个color就表示的新图片

Experimental steps :

K-Means Algorithm

1. 随机初始化： 从整个picture中随机选取16个pixel 作为初始化的迭代中心点。我采取的随机数方案可以实现不重复采样。

   function code:

   %% 随机选取初始点 return K * 3 
   function sample_Datas = sample_random(num,datas,dimx,dimy)
       % datas 为原始数据 num 为目标数目 
       sample_Datas = zeros(num,3);
       a = rand(dimx,1);
       b = rand(dimy,1);
       [vala,posa] = sort(a);
       [valb,posb] = sort(b);
       chose_x = posa(1:num,1);
       chose_y = posb(1:num,1);
       for i=1:num
           sample_Datas(i,:) = datas(chose_x(i),chose_y(i),:);
       end
   end
   

2. 计算每个Pixel的最邻近点： 遍历每个像素，每个pixel都有一个$RGBvector$ 并且$size=3\times 1$ 然后和 所有中心点求距离，选最小距离对应的中心点的K 作为这个pixel的class

   

   function code:

   %% 计算每个pixel 的 类别 return Clusters: N * N val 为 类别 
   function Clusters = calculate_Ci(centroids,dimx,dimy,datas,K)
       Clusters = [];
       % 遍历每个pixel 计算一个z(i,j)
       for i= 1:dimy
           for j = 1:dimx
               % 得到xi
               pixel_rgb = [datas(i,j,1),datas(i,j,2),datas(i,j,3)];
               diff = ones(K,1)*pixel_rgb - centroids;
               distance = sum(diff.^2,2);
               [~,class] = min(distance); % 得到最小的对应的类别的index
               Clusters(i,j) = class;
           end
       end
   end
   

3. 更新中心点$\mu$ 通过

​ Function code:

​

%% 更新中心点 return 16 * 3
function newcenters = updatemeans(Clusters,dimx,dimy,dimz,datas,K)
    newcenters = zeros(K,dimz);
    nums =  zeros(K);
    sumred = zeros(K,1);
    sumgreen = zeros(K,1);
    sumblue = zeros(K,1);
    for i=1:dimx
        for j=1:dimy
            class = Clusters(i,j);
            nums(class) = nums(class) + 1;
            sumred(class) = sumred(class) + datas(i,j,1);
            sumgreen(class) = sumgreen(class) + datas(i,j,2);
            sumblue(class) = sumblue(class) + datas(i,j,3);
        end
    end
    for i=1:K
        if nums(i) ~= 0
            sumred(i) = sumred(i) / nums(i);
            sumgreen(i) = sumgreen(i) / nums(i);
            sumblue(i) = sumblue(i) / nums(i);
        end
    end
    newcenters = [sumred,sumgreen,sumblue];
    newcenters = round(newcenters);
end

4. 判断收敛：

   我设定了最大收敛次数为150次，或者根据所有中心点更新前后的平方之和如果<$10^{-5}$就认为是没变化了，收敛了。

编程实现上述过程，最后得到 每个像素点对应的**$Clusters,size=N\times N$** 以及 每个中心点的RGB值：$Centroids,size=K\ast 3$

Reassigning Colors to The Large Image

​ 在这里，我分别对小图和大图都进行了处理。

​ 小图片：即对每个pixel 转化为 对应的class 的 RGB 值

​ 大图片：首先计算每个pixel 和 训练出来的中心点的最临近点，然后更换RGB值，得到新图片。

​ 随机一次初始值的效果：

​ 小图片：

大图片：分辨率更高

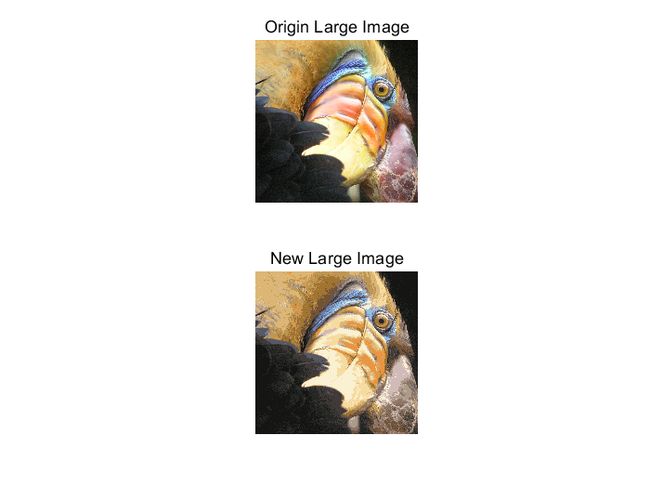
Choosing A Good Initial Point

选择一个好的初始点，为此我对上述过程进行循环，设定次数。意在选一个比较好的初始点。

每次计算出最后的图片之后，与原图进行逐一pixel的rgb差值求解，然后对RGB进行平方均值，计算出Loss，得到最低loss 的图片

作为Best New Small / Large Image

效果如下：

小图片：

大图片：

与原图对比一下，效果不错：

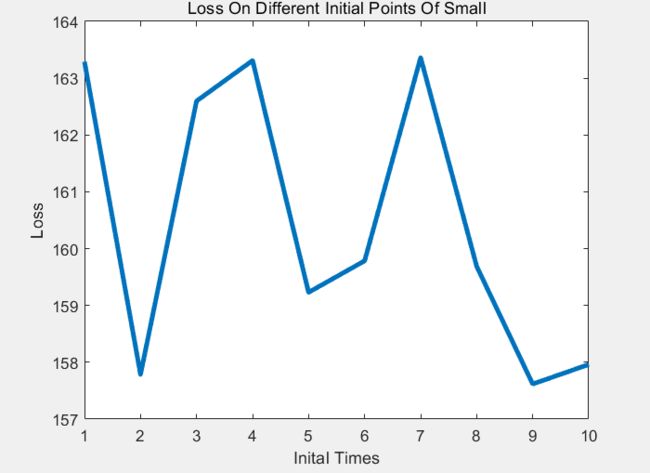
同时记录以下Loss 和 不同次进行随机初始的关系，画出图表：

可以看出：整体效果与初始点的初始有关系，可能存在Local Mininum

结论分析与体会

K-Means 整体算法架构

​ 即：

​ 每次固定中心点，然后更新每个点的类别

​ 或者固定每个点的类别，据此来更新中心点位置信息

Some Limitations Of K-Means

K-Means 具有适用范围：

• 适用于每个cluster 规模差不多，此时效果会不错
• 在round-shaped 的效果好

同时在non-convex shaped 表现不好

Kernel K-Means

即进行高维映射，以此来解决non-convex问题。同时仍不会显式投影，而是用 $K$

Hierarchical Clustering

层次聚类，bottom-up、top-down

实验源代码

Lab61.m

clear,clc
%% K-means
% small_img : 128 * 128 * 3
% large_img : 538 * 538 * 3
small_img = imread('bird_small.tiff');
large_img = imread('bird_large.tiff');
% 转化为double 矩阵 A(50,33,3) 表示 y = 50 x =33 的Blue 的val
small_img_matrix = double(small_img);
large_img_matrix = double(large_img);
%% show image 
% imshow(large_img)
%%
K = 16; % 16个class
[small_dimx,small_dimy,small_dimz] = size(small_img_matrix);
[large_dimx,large_dimy,large_dimz] = size(large_img_matrix);
max_iter_times = 200;
convergence_condition = 10^-5;
[centroids,Clusters] = kmeans(K,small_img_matrix,max_iter_times,convergence_condition);
%% 重新展示小图片
new_small_pic=[];
new_large_pic=[];
% 小图片处理
for i=1:small_dimx
    for j=1:small_dimy
        new_small_pic(i,j,:) =  centroids(Clusters(i,j),:);
    end
end

% 大图片处理
for i=1:large_dimy
    for j=1:large_dimy
        pixel_rgb = [large_img_matrix(i,j,1),large_img_matrix(i,j,2),large_img_matrix(i,j,3)];
        diff = ones(K,1)*pixel_rgb - centroids;
        distance = sum(diff.^2,2);
        [~,class] = min(distance); % 得到类别
        new_large_pic(i,j,:) =  centroids(class,:);
    end
end
%% 展示小图片 和 大图片
figure
subplot(2,1,1);
imshow(uint8(small_img_matrix)),title('Origin Small Image');
subplot(2,1,2);
imshow(uint8(new_small_pic)),title('New Small Image')
%% 
figure
subplot(2,1,1);
imshow(uint8(large_img_matrix)),title('Origin Large Image');
subplot(2,1,2);
imshow(uint8(new_large_pic)),title('New Large Image')
%% K-Means Fuction Return ?
function [centroids,Clusters] = kmeans(K,datas,max_iter_times,convergence_condition)
    % 返回中心点 K * dimz
    centroids = [];
    [dimy,dimx,dimz] = size(datas);
    % 随机初始化中心点 K*3
    centroids = sample_random(K,datas,dimx,dimy);
    for it = 1 : max_iter_times
        % 计算its nearest mean
        Clusters = calculate_Ci(centroids,dimx,dimy,datas,K);
        % 更新中心点
        new_centroids = updatemeans(Clusters,dimx,dimy,dimz,datas,K);
        % 看是否收敛
        convergence = judge(new_centroids,centroids,convergence_condition);
        centroids = new_centroids;
        if convergence
            break
        end
    end
end

%% 随机选取初始点 return K * 3 
function sample_Datas = sample_random(num,datas,dimx,dimy)
    % datas 为原始数据 num 为目标数目 
    sample_Datas = zeros(num,3);
    a = rand(dimx,1);
    b = rand(dimy,1);
    [vala,posa] = sort(a);
    [valb,posb] = sort(b);
    chose_x = posa(1:num,1);
    chose_y = posb(1:num,1);
    for i=1:num
        sample_Datas(i,:) = datas(chose_x(i),chose_y(i),:);
    end
    
end

%% 计算每个pixel 的 类别 return Clusters: N * N val 为 类别 
function Clusters = calculate_Ci(centroids,dimx,dimy,datas,K)
    Clusters = [];
    % 遍历每个pixel 计算一个z(i,j)
    for i= 1:dimy
        for j = 1:dimx
            % 得到xi
            pixel_rgb = [datas(i,j,1),datas(i,j,2),datas(i,j,3)];
            diff = ones(K,1)*pixel_rgb - centroids;
            distance = sum(diff.^2,2);
            [~,class] = min(distance); % 得到最小的对应的类别的index
            Clusters(i,j) = class;
        end
    end
end

%% 更新中心点 return 16 * 3
function newcenters = updatemeans(Clusters,dimx,dimy,dimz,datas,K)
    newcenters = zeros(K,dimz);
    nums =  zeros(K);
    sumred = zeros(K,1);
    sumgreen = zeros(K,1);
    sumblue = zeros(K,1);
    for i=1:dimx
        for j=1:dimy
            class = Clusters(i,j);
            nums(class) = nums(class) + 1;
            sumred(class) = sumred(class) + datas(i,j,1);
            sumgreen(class) = sumgreen(class) + datas(i,j,2);
            sumblue(class) = sumblue(class) + datas(i,j,3);
        end
    end
    for i=1:K
        if nums(i) ~= 0
            sumred(i) = sumred(i) / nums(i);
            sumgreen(i) = sumgreen(i) / nums(i);
            sumblue(i) = sumblue(i) / nums(i);
        end
    end
    newcenters = [sumred,sumgreen,sumblue];
    newcenters = round(newcenters);
end

%% 判断是否收敛
function convergence = judge(newcenter,oldcenter,condition)
    convergence = 0;
     d = sum(sqrt(sum((newcenter - oldcenter).^2, 2)));
    if d < condition
        convergence = 1;
    end
end

%% 返回行列坐标
function [row,col] = findrc(Clusters,val)
    [dimx,dimy] = size(Clusters);
    row = [];
    col = [];
    for i=1:dimx
        for j=1:dimy
            if Clusters(i,j) == val
                row = [row;i];
                col = [col;j];
            end
        end
    end
end

Lab62.m (多次迭代选最好效果)

clear,clc
%% 多进行几次，目的是初始点不同，找一个效果最好的。
%% K-means
% small_img : 128 * 128 * 3
% large_img : 538 * 538 * 3
small_img = imread('bird_small.tiff');
large_img = imread('bird_large.tiff');
% 转化为double 矩阵 A(50,33,3) 表示 y = 50 x =33 的Blue 的val
small_img_matrix = double(small_img);
large_img_matrix = double(large_img);
Best_new_small_pic=[];
Best_new_large_pic=[];
%% show image 
% imshow(large_img)
%%
inital_times = 10;
for inital_time = 1 : inital_times
    K = 16; % 16个class
    [small_dimx,small_dimy,small_dimz] = size(small_img_matrix);
    [large_dimx,large_dimy,large_dimz] = size(large_img_matrix);
    max_iter_times = 200;
    convergence_condition = 10^-5;
    [centroids,Clusters] = kmeans(K,small_img_matrix,max_iter_times,convergence_condition);
    %% 重新展示小图片
    loss_small = 1e9;
    loss_large = 1e9;
    new_small_pic=[];
    new_large_pic=[];
    % 小图片处理
    for i=1:small_dimx
        for j=1:small_dimy
            new_small_pic(i,j,:) =  centroids(Clusters(i,j),:);
        end
    end
    new_loss_small = calculate_Kmeans_Loss(small_img_matrix,new_small_pic,small_dimx,small_dimy);
    if new_loss_small < loss_small
        loss_small = new_loss_small;
        Best_new_small_pic = new_small_pic;
    end

    % 大图片处理
    for i=1:large_dimy
        for j=1:large_dimx
            pixel_rgb = [large_img_matrix(i,j,1),large_img_matrix(i,j,2),large_img_matrix(i,j,3)];
            diff = ones(K,1)*pixel_rgb - centroids;
            distance = sum(diff.^2,2);
            [~,class] = min(distance); % 得到类别
            new_large_pic(i,j,:) =  centroids(class,:);
        end
    end
    
    new_loss_large = calculate_Kmeans_Loss(large_img_matrix,new_large_pic,large_dimy,large_dimx);
    if new_loss_large < loss_large
        loss_large = new_loss_large;
        Best_new_large_pic = new_large_pic;
    end
end
%% 展示小图片 和 大图片
figure
subplot(2,1,1);
imshow(uint8(small_img_matrix)),title('Origin Small Image');
subplot(2,1,2);
imshow(uint8(Best_new_small_pic)),title('Best New Small Image')
imwrite(uint8(Best_new_small_pic),'Best New Small Image.png')

figure
subplot(2,1,1);
imshow(uint8(large_img_matrix)),title('Origin Large Image');
subplot(2,1,2);
imshow(uint8(Best_new_large_pic)),title('Best New Large Image')
imwrite(uint8(Best_new_large_pic),'Best New Large Image.png')
%% K-Means Fuction Return ?
function [centroids,Clusters] = kmeans(K,datas,max_iter_times,convergence_condition)
    % 返回中心点 K * dimz
    centroids = [];
    [dimy,dimx,dimz] = size(datas);
    % 随机初始化中心点 K*3
    centroids = sample_random(K,datas,dimx,dimy);
    for it = 1 : max_iter_times
        % 计算its nearest mean
        Clusters = calculate_Ci(centroids,dimx,dimy,datas,K);
        % 更新中心点
        new_centroids = updatemeans(Clusters,dimx,dimy,dimz,datas,K);
        % 看是否收敛
        convergence = judge(new_centroids,centroids,convergence_condition);
        centroids = new_centroids;
        if convergence
            break
        end
    end
end

%% 随机选取初始点 return K * 3 
function sample_Datas = sample_random(num,datas,dimx,dimy)
    % datas 为原始数据 num 为目标数目 
    sample_Datas = zeros(num,3);
    a = rand(dimx,1);
    b = rand(dimy,1);
    [vala,posa] = sort(a);
    [valb,posb] = sort(b);
    chose_x = posa(1:num,1);
    chose_y = posb(1:num,1);
    for i=1:num
        sample_Datas(i,:) = datas(chose_x(i),chose_y(i),:);
    end
    
end

%% 计算每个pixel 的 类别 return Clusters: N * N val 为 类别 
function Clusters = calculate_Ci(centroids,dimx,dimy,datas,K)
    Clusters = [];
    % 遍历每个pixel 计算一个z(i,j)
    for i= 1:dimy
        for j = 1:dimx
            % 得到xi
            pixel_rgb = [datas(i,j,1),datas(i,j,2),datas(i,j,3)];
            diff = ones(K,1)*pixel_rgb - centroids;
            distance = sum(diff.^2,2);
            [~,class] = min(distance); % 得到最小的对应的类别的index
            Clusters(i,j) = class;
        end
    end
end

%% 更新中心点 return 16 * 3
function newcenters = updatemeans(Clusters,dimx,dimy,dimz,datas,K)
    newcenters = zeros(K,dimz);
    nums =  zeros(K);
    sumred = zeros(K,1);
    sumgreen = zeros(K,1);
    sumblue = zeros(K,1);
    for i=1:dimx
        for j=1:dimy
            class = Clusters(i,j);
            nums(class) = nums(class) + 1;
            sumred(class) = sumred(class) + datas(i,j,1);
            sumgreen(class) = sumgreen(class) + datas(i,j,2);
            sumblue(class) = sumblue(class) + datas(i,j,3);
        end
    end
    for i=1:K
        if nums(i) ~= 0
            sumred(i) = sumred(i) / nums(i);
            sumgreen(i) = sumgreen(i) / nums(i);
            sumblue(i) = sumblue(i) / nums(i);
        end
    end
    newcenters = [sumred,sumgreen,sumblue];
    newcenters = round(newcenters);
end

%% 判断是否收敛
function convergence = judge(newcenter,oldcenter,condition)
    convergence = 0;
     d = sum(sqrt(sum((newcenter - oldcenter).^2, 2)));
    if d < condition
        convergence = 1;
    end
end

%% 计算K-Means 之后的图片的loss：计算所有pixel的rgb sum 然后 avg
function Loss1 = calculate_Kmeans_Loss(ori_img,new_img,dimx,dimy)
    Loss = zeros(3,1);
    div_num = dimx*dimy;
    for i=1:dimx
        for j = 1 :dimy
            Loss(1) = Loss(1) + (ori_img(i,j,1)-new_img(i,j,1)).^2 / div_num;
            Loss(2) = Loss(2) + (ori_img(i,j,2)-new_img(i,j,2)).^2 / div_num;
            Loss(3) = Loss(3) + (ori_img(i,j,3)-new_img(i,j,3)).^2 / div_num;
        end
    end
    Loss1 = sum(Loss) / 3;
end

n

    convergence = 1;
end

end

%% 计算K-Means 之后的图片的loss：计算所有pixel的rgb sum 然后 avg
function Loss1 = calculate_Kmeans_Loss(ori_img,new_img,dimx,dimy)
Loss = zeros(3,1);
div_num = dimx*dimy;
for i=1:dimx
for j = 1 :dimy
Loss(1) = Loss(1) + (ori_img(i,j,1)-new_img(i,j,1)).^2 / div_num;
Loss(2) = Loss(2) + (ori_img(i,j,2)-new_img(i,j,2)).^2 / div_num;
Loss(3) = Loss(3) + (ori_img(i,j,3)-new_img(i,j,3)).^2 / div_num;
end
end
Loss1 = sum(Loss) / 3;
end