AutoZOOM: Autoencoder-based Zeroth Order Optimization Method for Attacking Black-box Neural Networks

AutoZOOM: Autoencoder-based Zeroth Order Optimization Method for Attacking Black-box Neural Networks

Abstract

最近的研究表明，当目标模型被称为白盒设置（white box setting）时，由深度神经网络（DNN）训练的最先进图像分类器中的对抗样本可以很容易地生成。然而，当攻击已部署的机器学习服务时，只能获取目标模型的输入输出对应关系；这就是所谓的黑箱攻击设置。**现有黑盒攻击的主要缺点是需要过多的模型查询，这可能由于低效的查询设计而给模型健壮性带来错误的感觉。**为了弥补这一差距，我们提出了一个查询高效黑盒攻击的通用框架。我们的框架AutoZOOM是基于自动编码器的零阶优化方法的简称，它具有两个新的构造块，用于有效的黑盒攻击：（i）一种自适应随机梯度估计策略，用于平衡查询计数和失真，以及（ii）一种自动编码器，可以使用未标记的数据离线训练，也可以使用双线性调整操作来加速攻击。实验结果表明，通过将AutoZOOM应用于最先进的黑盒攻击（ZOO），可以显著减少模型查询，而不会牺牲攻击成功率和生成的对抗样本的视觉质量。特别是，与标准的ZOO方法相比，AutoZOOM可以在MNIST、CIFAR-10和ImageNet数据集上持续地将查找成功对抗样本（或达到相同失真水平）的平均查询数减少至少93%，从而对对抗性稳健性有了新的认识。

1 Introduction

近年来，”机器学习作为一种服务”为世界提供了一种不费吹灰之力就能完成各种任务的强大机器学习工具。例如，Google Cloud Vision API和Clarifai.com等商用服务为公众提供训练有素的图像分类器。允许以一个较低的价格上传图像和并获得预测分类。然而，现有和新兴的机器学习平台及其较低的模型访问成本引起了越来越多的安全问题，因为它们还提供了测试恶意尝试的理想环境。更糟糕的是，当这些服务用于构建衍生产品时，风险可能会被放大，攻击者可能会利用固有的安全漏洞。

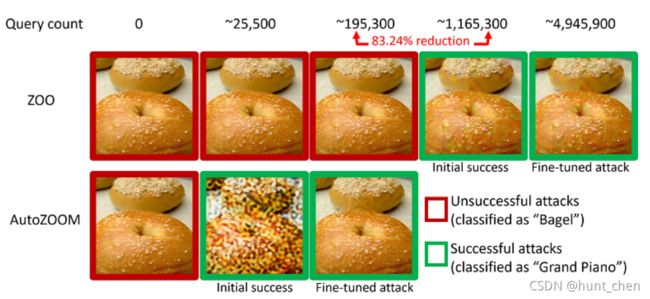
在许多计算机视觉任务中，DNN模型达到了最先进的预测精度，因此被广泛应用于现代机器学习服务中。尽管如此，最近的研究强调了DNN在对抗性干扰下的脆弱性。在目标模型对攻击者完全透明的白盒设置中，可以轻松制作视觉上不易察觉的敌对图像，通过利用输入梯度信息欺骗目标DNN模型进行错误分类（Szegedy et al.2014；Goodfello、Shlens和Szegedy 2015）。然而，在黑盒设置中，部署模型的参数是隐藏的，人们只能观察被查询样本的输入输出对应关系，制作对抗样本需要无梯度（零阶）优化方法来收集必要的攻击信息。图1显示了一个通过迭代模型查询从在ImageNet上训练的黑盒DNN（Inception - v3模型（Szegedy et al.2016））编制的预测规避对抗样本。

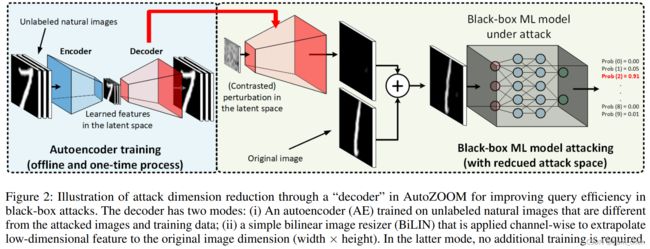
尽管通过使用梯度估计实现了显著的攻击效果，但当前的黑盒攻击方法，如（Chen等人2017；Nitin Bhagoji等人2018），由于利用坐标梯度估计和值更新，因此查询效率不高，这不可避免地会产生过多的模型查询，并且由于查询设计效率低下，可能会给模型健壮性带来错误的感觉。在本文中，我们建议使用基于自动编码器的零阶优化方法AutoZOOM来解决上述问题。AutoZOOM有两个新的构建模块：（i）一个新的自适应随机梯度估计策略，用于在制作对抗样本时平衡查询计数和失真；（ii）一个自动编码器，该编码器可以脱机对其他未标记数据进行训练，也可以基于简单的双线性调整操作，以加速黑盒攻击。如图2所示，AutoZOOM利用“解码器”从（学习到的）低维潜在空间表示中构建高维对抗性扰动，其查询效率可以通过无梯度优化中与维度相关的收敛速度得到很好的解释。

**贡献。**我们总结了我们在对抗鲁棒性方面的主要贡献和新见解，如下所示：

1. 我们提出了AutoZOOM，一种新的查询高效黑盒攻击框架，用于生成对抗样本。AutoZOOM采用自适应随机梯度估计策略和降维技术（离线训练的自动编码器或双线性重定器），以减少攻击查询计数，同时保持攻击有效性和视觉相似性。据我们所知，AutoZOOM是第一个使用随机全梯度估计和数据驱动加速的黑盒攻击。
2. 我们使用零阶优化的收敛速度来提高AutoZOOM的查询效率，并对AutoZOOM中的新梯度估计器进行了误差分析，以确定估计误差和查询计数之间的权衡。
3. 当应用于（Chen等人，2017年）中提出的最先进的黑盒攻击时，AutoZOOM获得了类似的攻击成功率，同时显著减少了攻击MNIST、CIFAR-10和ImageNet的DNN图像分类器所需的平均查询数（至少93%）。它还可以通过执行更精细的梯度估计来微调成功后阶段的失真。
4. 在实验中，我们还发现，使用简单的双线性重定器作为解码器（AutoZOOM BiLIN）的AutoZOOM可以获得显著的查询效率，尽管它仍然比使用离线训练的自动编码器（AutoZOOM AE）的AutoZOOM差。但是，AutoZOOM BiLIN更容易安装，因为不需要额外的培训。研究结果还表明，一个有趣的发现是，虽然学习合法图像的有效低维表示仍然是一项具有挑战性的任务，但使用明显较少自由度（即降低维度）的黑盒攻击肯定是可行的。

2 Related Work

基于梯度的对DNN的对抗性攻击属于白盒设置，因为获取关于输入的梯度需要知道目标DNN的权重。作为对黑盒攻击的第一次尝试，（Papernot et al.2017）中的作者建议使用迭代模型查询训练替代模型，对替代模型执行白盒攻击，并对目标模型实施转移攻击（Papernot、McDaniel和Goodfello 2016；Liu et al.2017）。然而，由于攻击可转移性差，其攻击性能可能会严重降低（Su等人，2018年）。尽管ZOO的攻击成功率和视觉质量与许多白盒攻击方法相似（Chen等人，2017），但其坐标梯度估计需要过多的目标模型评估，因此查询效率不高。同样的梯度估计技术也用于（Nitin Bhagoji等人，2018年）。

除了基于优化的方法外，（Ilyas等人，2018年）的作者还提出使用自然进化策略（NES）来提高查询效率。尽管在NES攻击中存在向量梯度估计步骤，但我们将其视为并行工作，因为其自然进化步骤超出了使用零阶梯度下降的黑盒攻击的范围。我们还注意到，与NES不同，我们的AutoZOOM框架使用了一种理论驱动的查询高效的基于随机向量的梯度估计策略。此外，自动缩放可以进一步提高网元的查询效率，因为网元没有考虑攻击降维的因素，这是自动缩放的新颖之处，也是本文的重点。

在更严格的攻击设置下，攻击者只知道决策（top-1预测类），在（Brendel、Rauber和Bethge 2018）中的作者提出了一种围绕决策边界的基于随机游走的攻击。这种黑盒攻击会分配类预测分数，因此需要额外的模型查询。由于篇幅限制，我们在补充资料中提供了更多的背景和一个比较现有黑盒攻击的表格。

3 AutoZOOM: Background and Method

3.1 Black-box Attack Fomulation and Zeroth Order Optimization

贯穿这篇文章，我们聚焦于通过AutoZOOM提高基于梯度估计和梯度下降的黑盒攻击的查询效率，且我们认为威胁模型（threat model）的类预测分数是为攻击者所知的。在此设定中，可以将目标DNN表示为一个分类函数$F:[0,1{]}^d\to {\mathbb{R}}^K$，它把一个d维度的图片（$d$-dimensional scaled image）作为输入，然后产出一个关于对所有$K$类图片的预测分数的向量，比如预测属于某一类的置信概率。我们还进一步考虑将初级(entry-wise)单调变换（monotonic transformation）$M(F)$应用于黑盒攻击的输出端 ，因为单调既变换保留了类预测的排序，又可以减轻的大分数变化（large score variation）的问题（e.g. 概率->对数概率）。

这里我们形式化了目标（targeted）黑盒攻击，这个公式同样也可以很好的适用于非目标攻击。$({\mathbf{x}}_0,t_0)$中的${\mathbf{x}}_0$表示自然（干净的）图像，$t_0$表示其所属的正确类别标签；$(\mathbf{x},t)$中的$\mathbf{x}$表示${\mathbf{x}}_0$的对抗样本，$t$表示目标类标签类别（$t\ne t_0$）。找到对抗样本这个问题可以形式化为一个优化问题，通用形式为
$$\underset{\mathbf{x}\in [0,1{]}^{\mathbf{d}}}{\min }\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}(\mathrm{x},{\mathrm{x}}_0)+\lambda \cdot \mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}(\mathrm{x},\text{M}(\text{F}(\mathrm{x}))\text{t})$$
$\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}(\mathrm{x},{\mathrm{x}}_0)$度量了自然图像$\mathrm{x}$和对抗样本${\mathrm{x}}_0$之间的失真程度（distortion）。$\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}(\cdot ）$是一个攻击目标，反映预测$t=\arg {\max }_{k\in \{1,\dots ,K\}}[M(F(x)){]}_k$的可能性。λ是正则化系数，约束$\mathrm{x}\in [0,1{]}^{\text{d}}$将对抗图像$\mathrm{x}$限制在有效图像空间内。自然图像$\mathrm{x}$和对抗样本${\mathrm{x}}_0$之间的失真程度$\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}(\mathrm{x},{\mathrm{x}}_0)$通常采用$L_p$来衡量，即对于$p\ge 1$有$\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}(\mathrm{x},{\mathrm{x}}_0)=||\mathrm{x}-{\mathrm{x}}_0|{|}_{\mathrm{p}}=||\mathbf{\delta }|{|}_{\mathrm{p}}={\sum }_{\mathrm{i}=1}^{\mathrm{d}}|{\mathbf{\delta }}_{\mathrm{i}}{|}^{\frac{1}{\text{p}}}$，$\mathbf{\delta }$是对原始图像的扰动且$\boldsymbol\delta = \rm x-x_0 $。攻击目标$\rm Loss(\cdot）$可以是DNNs的训练损失函数(Goodfellow, Shlens, and Szegedy 2015)或是基于模型预测的损失 (Carlini and Wagner 2017b)。

在白盒攻击设置中，通过使用诸如ADAM(Kingma and Ba 2015) 的下游优化器（downstream optimizer）解决（1），从而生成一个对抗样本；这就需要与通过反向传播在DNN中输入的$F$有关的目标函数$f(x)=\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}(\mathrm{x},{\mathrm{x}}_0)+\lambda \cdot \mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}(\mathrm{x},\text{M}(\text{F}(\mathrm{x})),\text{t}))$的梯度KaTeX parse error: Undefined control sequence: \grad at position 1: \̲g̲r̲a̲d̲ ̲f(x)。不过，在黑盒攻击设置中，获取KaTeX parse error: Undefined control sequence: \grad at position 1: \̲g̲r̲a̲d̲ ̲f(\cdot)是不可信的（implausible），只能得到函数的估计（evaluation）$F(\cdot )$，这使得求解（1）是一个零阶优化问题。最近，零阶优化方法 (Ghadimi and Lan 2013; Nesterov and Spokoiny 2017; Liu et al. 2018) 通过函数估计近似真实梯度，规避了上述挑战。具体的来说，在黑箱攻击求解（1）中，梯度估计既应用于梯度计算和下降，又应用于优化过程。

3.2 Random Vector based Gradient Estimation

作为首次尝试对DNN使用无梯度黑盒攻击的人，另一篇论文作者（Chen et al. 2017）使用对称差商方法（symmetric difference quotient method） (Lax and Terrell 2014）来评估DNN的第$i$个组成部分的梯度$\frac{\partial f(\mathrm{x})}{\partial {\mathrm{x}}_{\mathrm{i}}}$，如下：
$$g_i=\frac{f(\mathbf{x}+\text{h}{\mathbf{e}}_i)-f(\mathbf{x}-h{\mathbf{e}}_i)}{2h}\approx \frac{\partial f(\mathbf{x})}{\partial {\mathbf{x}}_i}$$
${\mathbf{e}}_i$表示第$i$个初等基，$h$时一个很小的数。尽管Chen的方法可以产生强大的黑盒攻击，且适用于像ImageNet这样的大型网络，但（2）中坐标梯度估计步骤的性质必须引起大量的模型查询，因此查询效率不高。例如，ImageNet数据集部分图片有$d=299\times 299\times 3\approx 270000$个输入维度，致使（rendering）基于梯度估计的坐标零阶优化查询效率低下。

为了提高查询效率，我们省去(dispense with)了坐标估计，提出了一种对KaTeX parse error: Undefined control sequence: \grad at position 1: \̲g̲r̲a̲d̲ ̲f(\mathbf x)的比例随机全梯度估计，定义为：
$$\mathbf{g}=b\cdot \frac{f(\mathbf{x}+\beta \mathbf{u})-f(\mathbf{x})}{\beta }\cdot \mathbf{u}$$
其中， $\beta >0$ 是一个平滑的参数，$\mathbf{u}$是一个从单位欧几里德球体均匀随机绘制的单位长度向量，$b$是可调缩放参数，用于权衡、平衡梯度估计误差的偏差和方差。

注意，如果$b=1$，则（3）中的梯度估计器与 (Duchi et al. 2015).中使用的梯度估计器一模一样。当$b=d$时，该估计器又会成为(Gao, Jiang, and Zhang 2014)中所采用的。在下面的分析中，我们将为平衡查询效率和估计误差提供一个最佳值$b$ （此处b右上角有一个*，不知道是什么意思，应该是有出处但没找到）。

平均随机梯度估计。为了有效地控制梯度估计中的误差，我们考虑更通用的梯度估计器，其中梯度估计在$q$个随机方向$\{{\mathbf{u}}_j{\}}_{j=1}^q$上平均，即：
$$\overline{\mathbf{g}}=\frac{1}{q}\sum _{j=1}^q{\mathbf{g}}_j$$
其中${\mathbf{g}}_j$是当${\mathbf{u}=\mathbf{u}}_j$时公式(3)中定义的一个梯度估计。对于凸损失函数，使用多个随机方向可以减少$\overline{\mathbf{g}}$的方差。(Duchi et al. 2015; Liu et al. 2018)

下面我们建立了关于（4）中平均随机梯度估计器的误差分析，以研究参数$b$和$q$对估计误差和查询效率的影响。

定理1： 假设： $f:{\mathbb{R}}^d\to \mathbb{R}$是可微的，它的梯度KaTeX parse error: Undefined control sequence: \grad at position 1: \̲g̲r̲a̲d̲ ̲f( \cdot)是L-Lipschitz[^1]的。则（4）中的 $\overline{\mathbf{g}}$ 的均方估计误差可以由以下表达式确定上界：
KaTeX parse error: Undefined control sequence: \grad at position 36: …e{ \mathbf{g}}-\̲g̲r̲a̲d̲ ̲f\mathbf{(x)}||…
证明：证明在supplementary file中给出

在这里，我们强调了基于定理1的重要隐含点：

（i）误差分析成立当$f$是非凸函数时（$误差分析成立\to f是非凸函数$）（ii）在DNNs中，真实梯度KaTeX parse error: Undefined control sequence: \grad at position 1: \̲g̲r̲a̲d̲ ̲f可视为通过反向传播获得的数值梯度；（iii）对于任何固定的$b$，选择一个小的$\beta$（例如，我们在AutoZOOM中设置$\beta =1/d$）可以有效地减少（5）中的最后一个误差项，也因此我们重点优化第一个误差项；（iv）（5）中的第一个误差项显示了$b$和$q$对估计误差的影响，并且独立于$\beta$。我们之后会进一步阐述（iv）。固定$q$，然后让$\eta (b)=\frac{b^2}{d^2}+\frac{b^2}{dq}+\frac{(b-d{)}^2}{d^2}$代替（5）中第一个误差项的系数，然后能使$\eta (b)$最小化的最优$b^{\ast }==\frac{dq}{2q+d}$。为了提高查询效率，我们希望较小的$q$值，这意味着$b^{\ast }\approx q$且当维度$d$较大时 $\eta (b^{\ast })\approx 1$ 。另一方面，当$q\to \infty ,b^{\ast }\approx d/2$且$\eta (b^{\ast })\approx 1/2$，这虽然会产生更小的错误上限，但查询效率较低。我们还注意到当设置$b=q$时，第一个误差项的系数 $\eta (b)=\frac{b^2}{d^2}+\frac{b^2}{dq}+\frac{(b-d{)}^2}{d^2}\approx 1$ ，因此与维度$d$和参数$q$无关。

自适应随机梯度估计。基于定理1和我们的误差分析，在AutoZOOM中，我们在（5）中设置 $b=q$ ，并提出使用自适应策略进行选择 $q$ 。AutoZOOM使用$q=1$（i.e.，尽可能少的模型评估）首先获得用于求解（1）的粗略梯度估计直到找到成功的敌方图像。初始攻击成功后，它将切换到使用更精确的梯度估计值（$q>1$）来微调图像质量。第4节将研究 $q$ （与查询计数成比例）和失真减少之间的权衡。

3.3 Attack Dimension Reduction via Autoencoder

**使用梯度估计的维度依赖收敛率。**与一阶收敛结果不同，零阶梯度下降法的收敛速度有一个额外的相乘的维数依赖因子$d$。在凸损失（convex loss）中设置（收敛）速度为 $O(\sqrt{d/T})$ ， $T$ 是迭代次数（Nesterov and Spokoiny 2017; Liu et al. 2018; Gao, Jiang, and Zhang 2014; Wang et al. 2018）。在非凸的设置中也找到了同样的设置 (Ghadimi and Lan 2013)。与维数相关的收敛因子$d$表明，当（矢量化的）图像维数$d$较大时，由于收敛中的维数灾难(curse of dimensionality)，使用梯度估计的普通黑盒攻击会是低效的。这也促使我们提出在黑盒攻击中使用自动编码器来降低攻击维数并提高查询效率。

在AutoZOOM中，我们在降低的维数 $d’<d$ 执行随机梯度估计，从而提高查询效率。具体来说，如图2所示，针对DNN上的黑盒攻击，对图像${\mathrm{x}}_0$的附加扰动实际上是通过“解码器” $D:\mathbb{R}\to {\mathbb{R}}^d$ 使得 $\mathrm{x}={\mathrm{x}}_0+\text{D}({\mathbf{\delta }}^{\prime })$ 实现的，其中 ${\mathbf{\delta }}^{\prime }\in {\mathbb{R}}^{d^{\prime }}$ 。也就是说，对${\mathrm{x}}_0$的对抗性扰动 $\mathbf{\delta }\in {\mathbb{R}}^d$ 实际上是从降维空间生成的，其目的是提高查询效率（根据降低之前收敛分析中的降维依赖因子 $d$ ）。AutoZOOM为这种解码器$D$提供了两种模式：

• 在一组与训练数据不同无标签数据上训练的的自动编码器（AE），用于学习从降维表示中重建。AE中的编码器$E(\cdot )$将数据压缩到低维潜在（latent）空间，解码器$D(\cdot )$从这个（低维）潜在表示重构样本。AE中的权重线朝着最小化平均$L2$重建误差的方向学习。注意：针对黑盒对抗性攻击训练此类AE是一次性的，并且完全离线（i.e.，不需要模型查询）。
• 一个简单的通道双线性图像大小调整器（BiLIN），可以通过双线性外极（extrapolation）将小图像缩放为大图像。请注意，BiLIN不需要额外的训练。

**为什么是AE？**我们之所以建议$\mathrm{A}\mathrm{E}$，是因为(Goodfellow, Shlens, and Szegedy 2015)中的深刻发现：一个成功的对抗干扰与某些类似于目标类形状的、人类不易察觉的噪声模式高度相关，称之为“阴影”（shadow）。由于$ \rm AE$中的解码器学习从潜在表示重构数据，因此它还可以为映射对抗扰动以生成这些阴影提供分布指导。

我们还注意到，对于任何降维 （后的维度）$d^{\prime }$ ，要最小化定理1中相应的估计误差，$b^{\ast }=q$ 是最优的设置，尽管事实上不同的降维下梯度估计误差不能直接比较。在第4节中，我们将报告使用$\mathrm{A}\mathrm{E}$或$\mathrm{B}\mathrm{i}\mathrm{L}\mathrm{I}\mathrm{N}$作为解码器在黑盒攻击中的优越查询效率，并讨论攻击降维的好处。

3.4 AutoZOOM Algorithm

算法1 AutoZOOM在DNN上的黑盒攻击

**输入：**黑盒DNN模型$F$，原始样本${\mathrm{x}}_0$。失真量化函数$\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}(\cdot )$，攻击目标损失函数$\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}(\cdot )$，单调变换函数$M(\cdot )$，解码器$D(\cdot )\in \mathrm{A}\mathrm{E},\mathrm{B}\mathrm{i}\mathrm{L}\mathrm{I}\mathrm{N}$，初始系数${\lambda }_{\mathrm{i}\mathrm{n}\mathrm{i}}$，和查询预算$Q$。

while 查询次数 $\le Q$，do

​ **1. 探索：**使用$\mathrm{x}={\mathrm{x}}_0+\mathrm{D}({\mathbf{\delta }}^{\prime })$和（4）中的随机梯度估计器（$q=1$）到下游优化器（如ADAM），解决（1）知道首个攻击被找到。

​ **2. 开发（exploitation）（后成功阶段）：**继续调整对抗扰动$D({\mathbf{\delta }}^{\prime })$以解决（1）直到可以在（4）中设置$q>1$

end while

**输出：**最小失真的成功对抗样本

算法1总结了AutoZOOM对于在DNNs上进行高效查询黑盒攻击的框架，我们还注意到AutoZOOM是一个通用的加速工具，可以与任何遵循（1）的基于梯度估计的黑盒对抗攻击相容。它还具有一些理论上的估计误差保证，并根据定理1选择查询高效的参数。第4节将讨论基于运行时模型评估结果调整正则化系数$\lambda$和查询参数$q$的细节。代码公开在github¹上。

4 Performance Evaluation

本节介绍了根据第一次攻击成功所需的查询数量和特定失真级别，评估AutoZOOM在加速DNN黑盒攻击中的性能的实验。

4.1 Distortion Measure and Attack Objective

如第3节所述，AutoZOOM是一个高效的无梯度优化框架，用于解决（1）中的黑盒攻击公式。在以下实验中，我们使用ZOO（Chen等人，2017）提出的相同攻击公式证明了AutoZOOM的实用性（utility），该公式使用平方 $L_2$ 范数作为失真量化函数 $\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{t}(\cdot )$ ，并采用攻击目标
$$\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}=\max \{\underset{\mathrm{j}\ne \mathrm{t}}{\max }\log [\text{F}(\mathrm{x}){]}_{\mathrm{j}}-\log [\text{F}(\mathrm{x}){]}_{\mathrm{t}}\},0\}$$

其中这个Hinge函数是为在DNN模模型$F$上的目标黑盒攻击设计的，且在模型输出端使用单调变化(函数)$M(\cdot )=log(\cdot )$。

4.2 Comparative Black-box Attack Methods

我们两种不同的基线比较了AutoZOOM-AE $(D=AE)$ 和AutoZOOM-BiLIN $(D=\mathrm{B}\mathrm{i}\mathrm{L}\mathrm{I}\mathrm{N})$ ：(i)使用双线性缩放（与BiLIN相同）进行降维实现的标准ZOO² (ii)ZOO+AE，即有AE的ZOO。请注意，所有攻击会基于相同的降低攻击维度产生对抗性干扰。

4.3 Experiment Setup, Evaluation, Datasets and AutoZOOM Implementation

我们评估了几种典型基准数据集上不同攻击方法的性能，包括MNIST（LeCun et al.1998）、CIFAR-10（Krizhevsky 2009）和ImageNet（Russakovsky et al.2015）。对于MNIST和CIFAR-10，我们使用与（Carlini和Wagner 2017b）中相同的DNN图像分类模型³。对于ImageNet，我们使用Inception-v3模型（Szegedy等人，2016）。所有实验均使用TensorFlow机器学习库，在配备Intel Xeon E5-2690v3 CPU和Nvidia Tesla K80 GPU的机器上进行。

所有攻击都使用其估计梯度和ADAM求解$(1)$，且学习率都被相同的初始化为 $2\times 10^{-3}$ 。在MNIST和CIFAR-10上，所有方法都采用1000次ADAM迭代。在ImageNet上，ZOO和 ZOO+AE 采用20000次迭代，而AutoZOOM BiLIN和AutoZOOM AE采用100000次迭代。请注意，由于梯度估计方法不同，每次黑盒攻击迭代的查询计数（即，模型评估的数量）可能会有所不同。ZOO和ZOO+AE使用$(2)$的并行梯度更新，一批128像素，每次迭代产生 $256$ 个查询计数。AutoZOOM BiLIN和AutoZOOM AE使用$(4)$中的平均随机全梯度估计器，每次迭代的结果为 $q+1$ 查询计数。为了进行公平比较，查询计数用于性能评估。

**查询缩减率。**我们使用具有最小 ${\lambda }_{\mathrm{i}\mathrm{n}\mathrm{i}}$ 的ZOO的平均查询计数作为基线来计算其他方法和配置的查询缩减率。

**TPR和初步成功。**我们报告了真实阳性率（TPR），它测量了满足对标准化（每像素） $L_2$ 失真的预定义约束 $\ell$ 的成功攻击的百分比，以及它们到首次成功的查询计数。我们还报告了初始成功的每像素 $L_2$ 失真，其中初始成功指的是第一次找到成功对抗样本的查询计数（原句是where an initial success refers to the first query count that finds a successful adversarial example，直译为“初始成功指的是找到成功对抗样本的第一次查询计数”，不太明白，有所改动）。

P.S. TPR就是检测出来的真阳性样本数除以所有真实阳性样本数。

$\mathrm{T}\mathrm{P}\mathrm{R}=\frac{满足约束\mathrm{\ell }的成功攻击数目}{所有的成功攻击数目}\times 100\%$

**成功后微调（fine-tuning）。**在MNIST和CIFAR-10上实现算法1的AutoZOOM时，我们发现无需微调（即 $q=1$ ）的AutoZOOM就已经产生与ZOO类似的失真。我们注意到，ZOO可以被视为坐标微调，因此查询效率低下。在ImageNet上，我们将研究成功后微调对减少失真的影响。

**自动编码器训练。**在AutoZOOM-AE中，我们使用卷积自动编码器进行攻击降维，该编码器在不同于训练数据集和被攻击自然样本的未标记数据集上进行训练。补充材料中给出了实施细节。

**动态切换 $\lambda$ 。**为了调整 $(1)$ 中的正则化系数 $\lambda$ ，在所有方法中，我们在MNIST和CIFAR-10上设置其初始值 $λ_{\rm ini}\in {0.1,1,10} $ ，在ImageNet上设置 ${\lambda }_{\mathrm{i}\mathrm{n}\mathrm{i}}=10$。此外，为了平衡 $(1)$ 中的失真距离和攻击目标损失，我们在优化过程中使用了动态切换 策略来更新 $\lambda$ 。如果攻击从未成功，则每 $S$ 次迭代， $\lambda$ 更新为当前值的10倍。否则，它更新为其当前值除以2。在MNIST和CIFAR-10上，我们设置 $S=100$ 。在ImageNet上，我们设置 $S=1000$ 。在初始成功的情况下，我们还将 $\lambda ={\lambda }_{\mathrm{i}\mathrm{n}\mathrm{i}}$ 和ADAM参数重置为默认值，因为根据经验，这样做可以减少所有攻击方法的失真。

4.4 Black-box Attacks on MNIST and CIFAR-10

于MNIST和CIFAR-10，我们从它们的测试集中随机选择50个正确分类的图像，并对这些图像执行有针对性的攻击。由于两个数据集都有10个类，因此每个选定的图像都会受到9次攻击（攻击对象为除了其正确标签之外的其他9个类别标签）。对于所有攻击，MNIST的缩减攻击空间维度为原始攻击空间维度（即 $d^{\prime }/d$ ）的25%，CIFAR-10则缩减为6.25%。

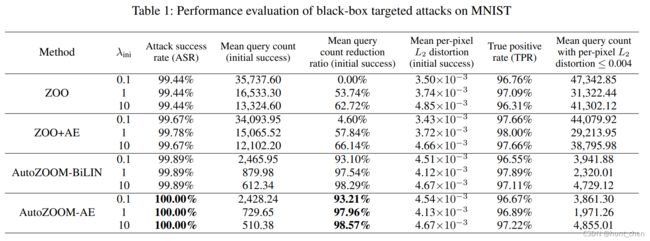
表1显示了在MNIST上使用各种 ${\lambda }_{\mathrm{i}\mathrm{n}\mathrm{i}}$ 值（即 $(1)$ 中正则系数 $\lambda$ 的初始值）的性能评估。我们使用 ${\lambda }_{\mathrm{i}\mathrm{n}\mathrm{i}}=0.1$ 的ZOO性能作为比较基准。例如，当 ${\lambda }_{\mathrm{i}\mathrm{n}\mathrm{i}}=0.1$ 和 $10$ 时，AutoZOOM-AE获得初始成功所需的平均查询数分别减少了93.21%和98.57%。我们还可以观察到，允许更大的 ${\lambda }_{\mathrm{i}\mathrm{n}\mathrm{i}}$ 通常会带来更少的平均查询计数，但是代价是初始攻击的失真会略微增加。AutoZOOM和ZOO/ZOO+AE之间所需的攻击查询计数的显著差异验证了我们在 $(3)$ 中提出的随机全梯度估计器的有效性，该估计器在ZOO中省去了坐标梯度估计，但仍然保持类似的（comparable）TPR，从而大大提高了查询效率。

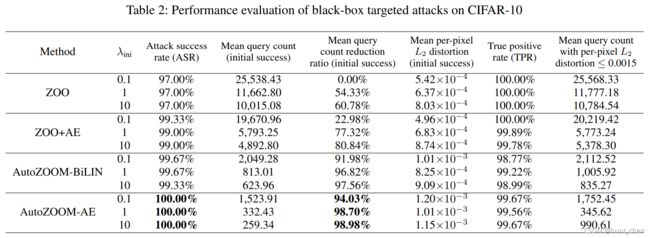
对于CIFAR-10，我们报告了如表2所示的类似的查询效率改进。特别是，通过比较两种查询效率高的黑盒攻击方法（AutoZOOM BiLIN和AutoZOOM-AE），我们发现AutoZOOM-AE比AutoZOOM-BiLIN具有更高的查询效率，但需要额外的AE训练步骤。对于不同的 ${\lambda }_{\mathrm{i}\mathrm{n}\mathrm{i}}$ 值，AutoZOOM-AE实现了最高的攻击成功率（ASR）和平均查询减少率。此外，它们的真阳性率（TPR）相似，但AutoZOOM-AE通常仅需较少的查询计数就能达到相同的 $L_2$ 失真。我们注意到，当 $\lambda \mathrm{i}\mathrm{n}\mathrm{i}=10$ 时，AutoZOOM-AE具有更高的TPR，但也需要比AutoZOOM BiLIN略多的平均查询计数才能达到相同的 $L2$ 失真。这表明存在部分对抗样本，双线性重定器很难减少它们成功后的失真，但可以由AE处理。

4.5 Black-box Attacks on ImageNet

我们从ImageNet测试集中选择了50张正确分类的图像来执行随机目标攻击，并设置 ${\lambda }_{\mathrm{i}\mathrm{n}\mathrm{i}}=10$ 和攻击降维率为1.15%。结果汇总在表3中。请注意，与ZOO相比，AutoZOOM-AE可以将获得初始成功所需的查询数显著减少99.39%（或99.35%以达到相同的 $L2$ 失真），这是一个显著的改进，因为这意味着减少了超过2.2m个维度，鉴于ImageNet的维度$(\approx 270K)$比MNIST和CIFAR-10大得多。

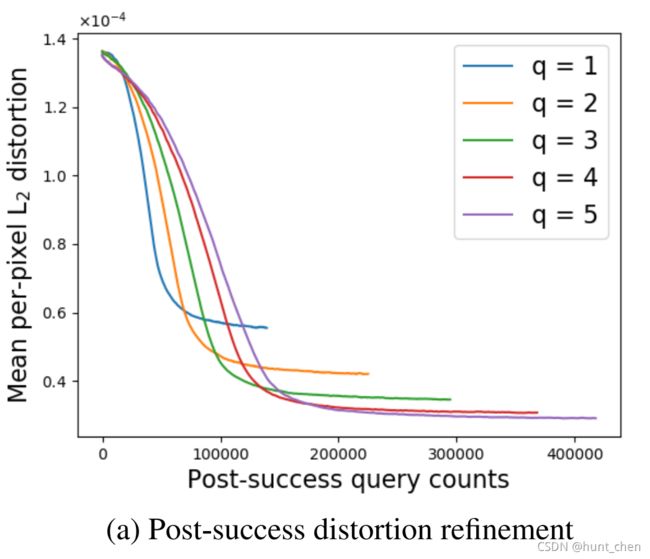
**成功后失真优化（refinement）。**如算法1所述，自适应随机梯度估计集成在AutoZOOM中，在攻击生成中提供快速的初始成功，然后进行微调过程以有效减少失真。这是通过在成功后阶段调整 $(4)$ 中的梯度估计平均参数 $q$ 来实现的。一般来说，在更多随机方向上求平均值（i.e.，设置更大的 $q$ 值）倾向于更好地减少梯度估计误差的方差，但代价是增加模型查询。图3（a）显示了在成功后阶段对 $q$ 的各种选择的平均失真随着查询计数的变化情况。结果表明，与 $q=1$ 的情况相比，设置一些小 $q(q>1)$ 可以进一步降低收敛阶段的失真。此外，在 $q=4$ 时，失真的优化效应（refinement effect）在经验上达到饱和，这意味着超出该值的边际增益（很小）。这些发现还表明，我们提出的自动缩放确实在黑盒攻击中的失真和查询效率之间取得了平衡。

4.6 Dimension Reduction and Query Efficiency

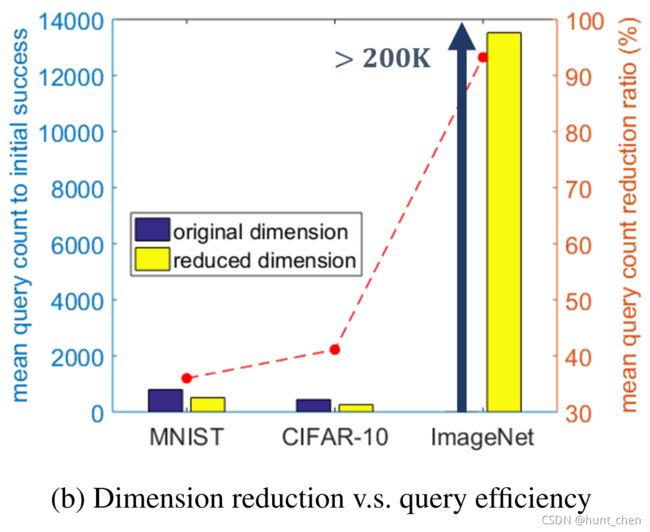
除了零阶优化中的收敛速度 $O(\sqrt{d/T})$ （第3.3节）的动机外，作为一种合理性（sanity）检查，我们通过比较AutoZOOM（此处我们使用 $D=AE$ ）及其在原始（未缩减）维度上的替代操作，证实(corroborate)了攻击维度缩减对黑盒攻击中查询效率的好处（即 ${\delta }^{\prime }=D(\delta 0^{\prime })=\delta$ ）。在所有三个数据集和上述(aforementioned：上述的)设置上进行测试，图3（b）显示所有三个数据集中 $ λ_{\rm ini}=10$ 时对应的初始成功平均查询数和平均查询缩减率。与原始维度的攻击结果相比，通过AutoZOOM进行的维度缩减的攻击在MNIST和CIFAR-10上大约减少了35-40%的查询数，在ImageNet上至少减少了95%。此结果强调了维度缩减对查询高效的黑盒攻击的重要性。例如，如果没有维度缩减，对原始ImageNet维度的攻击甚至无法在查询预算内成功（查询次数$Q=200K$）。

4.7 Additional Remarks and Discussion

• 除了初始攻击成功的基准测试外，当达到相同的 $L_2$ 失真时，可以直接从每个表的最后一列计算查询减少率。
• 与AutoZOOM-BiLIN相比，AutoZOOM-AE的攻击增益(attack gain)有时可能是微乎其微的，但我们也注意到，通过探索不同的AE模型，来改进AutoZOOM-AE。然而，在测试模型稳健性时，我们提倡将AutoZOOM-BiLIN作为查询效率高的黑盒攻击的理想候选，因为它易部署（easy-to-mount），并且没有额外的培训成本。
• 虽然学习合法图像的有效低维表示仍然是一项具有挑战性的任务，但如本文所示，使用明显较少自由度（即降低维度）的黑盒攻击无疑是可行的，从而对模型鲁棒性产生了新的影响。

5 Conclusion

AutoZOOM是一个通用的攻击加速框架，它与任何基于梯度估计的黑盒攻击（具有 $(1)$ 中的一般公式）兼容。它采用了一种新的自适应随机全梯度估计策略来平衡查询计数和估计误差，并具有一个解码器（AE或BiLIN）来减少攻击维数和加速算法收敛。与最先进的攻击（ZOO）相比，在攻击MNIST、CIFAT-10和ImageNet的黑盒DNN图像分类器时，AutoZOOM始终减少了平均查询数，在找到最初成功的对抗对抗样本（或达到相同的失真）时，查询数至少减少93%同时保持相似的攻击成功率。它还可以有效地微调图像失真，以保持与原始图像的高度视觉相似性。因此，AutoZOOM为评估已部署机器学习模型的鲁棒性提供了新颖有效的方法。

暴力的黑盒对抗样本攻击 – ZOO - 简书 (jianshu.com)
第一次读讲论文，太难受了。有问题兄弟萌告诉我一下。

---

1. https://github.com/IBM/Autozoom-Attack ↩︎

2. 标准ZOO代码仓库 ↩︎

3. 代码仓库 ↩︎