生成式模型和判别式模型、HMM
参考–图很好


根据训练数据得到分类函数和分界面,比如说根据SVM模型得到一个分界面,然后直接计算条件概率
判别式模型计算的是P(y|x)的最大概率作为分类–判别式模型是对条件概率建模,学习不同类别之间的最优边界,无法反映训练数据本身的特性,能力有限,其只能告诉我们分类的类别。
生成式模型计算的是P(x,y)作为联合概率作为分类。

因为P(x,y) = P(x|y) * P(y) :比如说类别标签有{猫,狗,猪},那首先根据猫的特征学习出一个猫的模型,再根据狗的特征学习出狗的模型,之后分别计算新样本 跟三个类别的联合概率-----p(X|Y)在狗/猫的模型下,选择X属性特征的概率。
总结


总之,判别式模型和生成式模型都是使后验概率最大化,判别式是直接对后验概率建模,而生成式模型通过贝叶斯定理这一“桥梁”使问题转化为求联合概率。
HMM
隐马尔可夫模型由初始状态矩阵Π;状态转移概率矩阵A以及观测概率矩阵B决定,初始状态矩阵Π;状态转移概率矩阵A决定状态序列,B决定观测序列。
其实HMM不难,主要就是观测序列,初始状态,状态转移之间的关系。
HMM包含三个基本问题:概率计算问题、预测问题、学习问题。
主要包括了 初始状态矩阵Π;状态转移概率矩阵A以及观测概率矩阵B—模型参数三个。
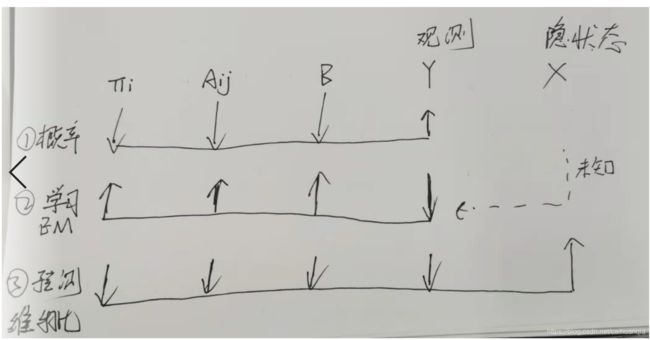
Y观测序列,X隐状态序列
1、概率计算问题:已知模型的所有参数,计算观测序列出现的概率,
可以使用前向算法和后向算法求解。—已知Π、A和B, 求Y出现的概率。
2、预测问题:已知模型的所有参数和观测序列Y,计算最有可能的隐状态序列X,可以使用动态规划—维特比算法求解最有可能的状态序列。—已知Π、A和B和Y,求概率最大的X。
3、学习问题:已知观测序列Y,求使得该观测序列概率最大的模型参数,包括隐状态序列、隐状态之间的转移概率分布以及从隐状态到观测状态的概率分布。使用Baum-Welch求解。------已知Y, 求Π、A和B。
1、概率计算问题–其实也就是简单的动态规划问题
动态规划–递归 由上一个状态推导到现在的状态。
前向算法和后向算法
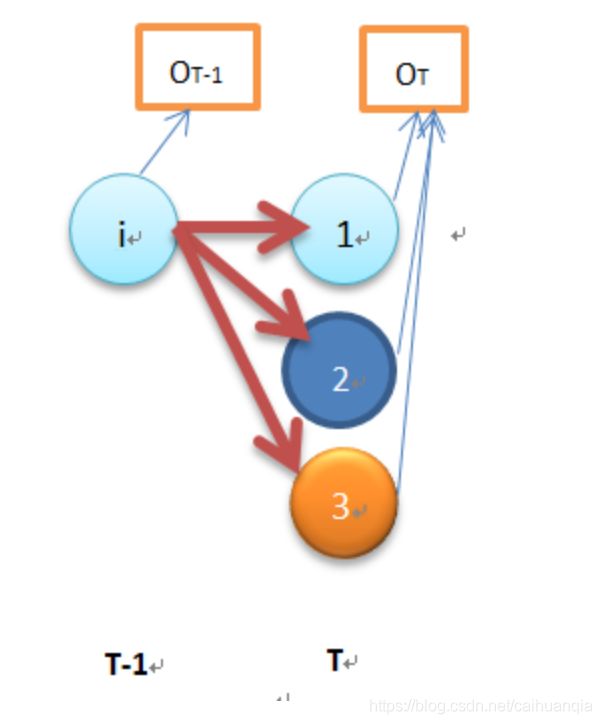
前向算法用下面的图可以较好表示,1、2、3分别表示不同的时间节点,上面的四个节点是四个状态,t时刻的状态i由t-1时刻的所有状态转移得到。最后计算出最后时刻的各个状态对应的 概率之和 就是取得 观测序列的概率。
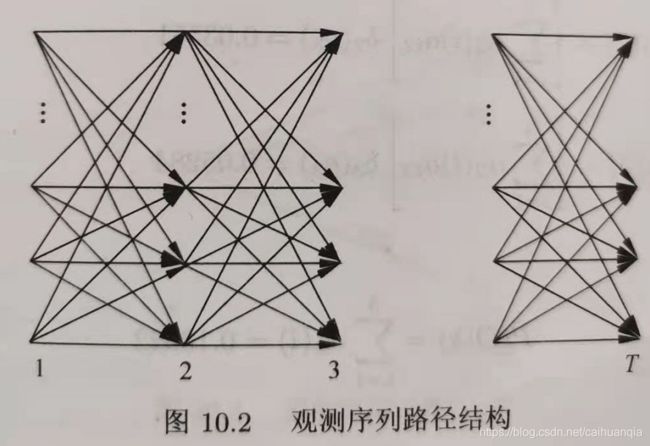
前向算法实例
后向算法
注意β的定义:在已知T时刻状态为qi,和模型三个参数的条件下,那么得到所有观测序列的概率必定是1.右边是已知的。等价于 == P(ot+1,ot+2…) == 1 观测也是已知的。

注意状态转移aij本就是可以相互转换的,有aij也有aji。
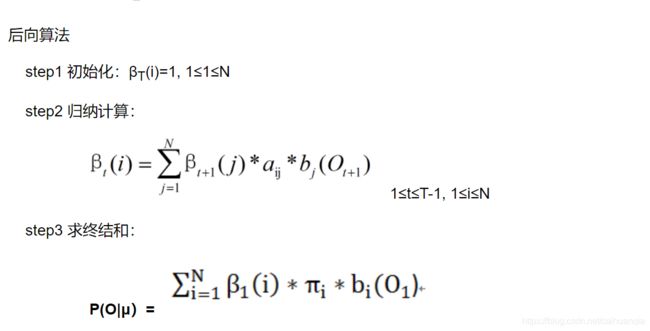

明确好β的含义就清楚最终时刻的β就是1—在时刻t,状态为si的前提下,输出观测序列的概率。
因为我们后推的每个状态仍然是假如最后一个状态选定的条件下逆向的,所以,到了时刻1,因为有初始概率,所以就可以计算出求得该观测序列的概率。
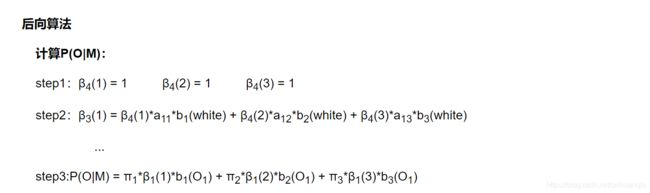
![]()
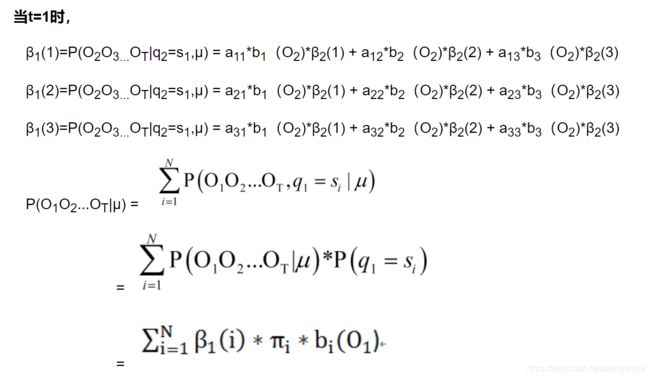

2、预测问题–维特比算法
维特比算法也就是动态规划求解最优路径。在给定观测序列和状态转移概率矩阵之下,求得最优的状态–也就是得到在此观测序列之下概率最大的状态。
动态规划要注意到,达到i节点的路径是最优的,那么达到i-1节点的路径也肯定是最优的。不然的话,从时刻1 – i-1的路径就有更优的路径,我们记录的是最优路径。
所以我们可以从t=1开始,递推计算在t时刻状态为i的各条部分路径的最大概率。
每一个时刻的I个状态都是从上一个时刻的I个状态转移过来的,然后取最优值。
原理很简单,但是看公式稍微费力。
—正常leetcode的解法即可。dp[i][j] — i代表时刻,j代表状态, b表示的是观测
转移矩阵: dp[i][j] = max(dp[i-1][0]*a[0,j] * b[i], dp[i-1][1]*a[1,j] * b[i] …)

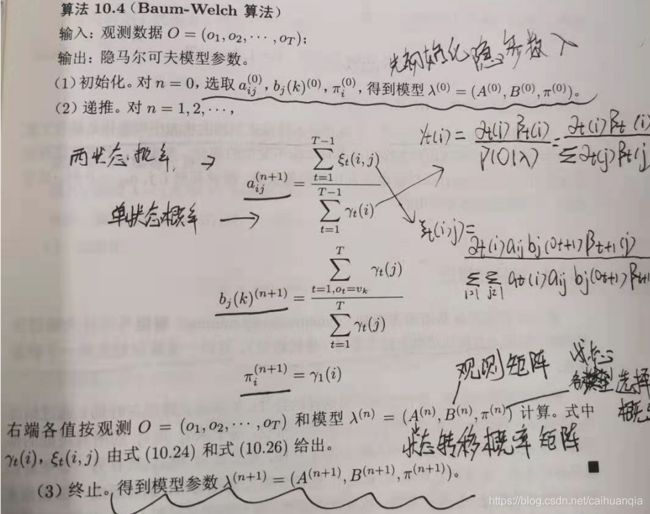
3、 学习问题
其实就是假设模型,然后使得P(O|A,B,Π )最大,即极大似然估计法。但是怎么假设得到模型,就是通过EM算法这种高效的方式进行。–把极大化的问题归结为Q函数,再通过最大化Q函数等价于使得P最大,求得的模型自然也满足了极大似然的要求。
学习问题其实是完完整整的EM算法的流程。—已知观测序列和对应的状态序列,求隐马尔可夫模型的参数。
模型的参数包括三个:A 状态转移概率矩阵、B 观测矩阵、Π 初始状态概率的估计。
详见统计机器学习P204,主要用到了拉格朗日乘子法来实现求导,使得对Q函数极大化。
其实学习问题也就是用到了EM算法,EM算法已经会推导,所以直接套用E得到的Q函数,然后对Q函数进行分解开来,得到三部分,我们的目的是极大化Q函数,因为要极大化的参数分别在三部分里,所以极大化各自的部分是等价的。这三部分分别也就是 A 状态转移概率矩阵、B 观测矩阵、Π 初始状态概率的估计。
通过引入拉格朗日乘子,添加原本的约束条件,再进行求导,令值为0,极大化,最终得到 参数的表达式。
引入拉格朗日乘子的目的是使得求导的结果同时也满足约束条件。