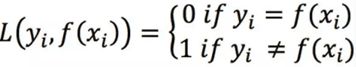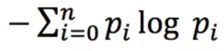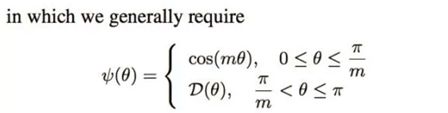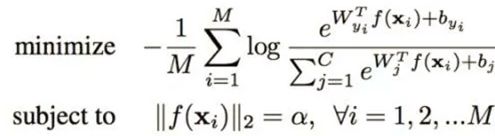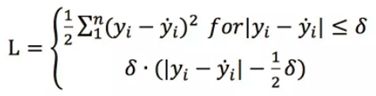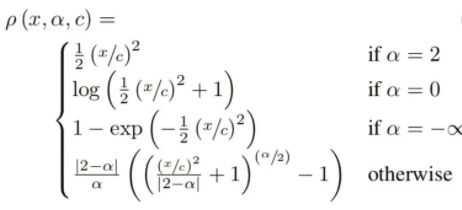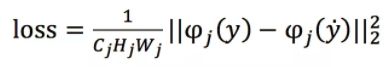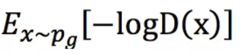扫盲记-第八篇--深度学习 之 损失函数学习

1 什么是损失函数

机器学习中的损失函数（loss function）是用来评估模型的预测值-f(x)与真实值-y的不一致程度，损失函数越小，代表模型的鲁棒性越好，损失函数能指导模型学习。

 

2 分类任务损失 

2.1、0-1 loss

0-1 loss是最原始的loss，它直接比较输出值与输入值是否相等，对于样本i，它的loss等于：

当标签与预测类别相等时，loss为0，否则为1。可以看出，0-1 loss无法对x进行求导，在依赖于反向传播的深度学习任务中，无法被使用，0-1 loss更多的是启发新的loss的产生。

2.2、熵与交叉熵loss

物理学中的熵，表示一个热力学系统的无序程度。为了解决对信息的量化度量问题，香农在1948年提出了“信息熵”的概念，它使用对数函数表示对不确定性的测量。熵越高，表示能传输的信息越多，熵越少，表示传输的信息越少，可以直接将熵理解为信息量。

按照香农的理论，熵背后的原理是任何信息都存在冗余，并且冗余大小与信息中每个符号（数字、字母或单词）的出现概率或者说不确定性有关。概率大，出现机会多，则不确定性小，这个关系就用对数函数来表征。

为什么选择对数函数而不是其他函数呢？首先，不确定性必须是概率P的单调递降函数，假设一个系统中各个离散事件互不相关，要求其总的不确定性等于各自不确定性之和，对数函数是满足这个要求的。将不确定性f定义为log(1/p)=-log(p)，其中p是概率。

对于单个的信息源，信源的平均不确定性就是单个符号不确定性-logp_i的统计平均值，信息熵的定义如下：

假设有两个概率分布p(x)和q(x)，其中p是已知的分布，q是未知的分布，则其交叉熵函数是两个分布的互信息，可以反应其相关程度。

至此，引出了分类任务中最常用的loss，即log loss，又名交叉熵loss，后统一称为交叉熵：

n对应于样本数量，m是类别数量，y_ij 表示第i个样本属于分类j的标签，它是0或者1。对于单分类任务，只有一个分类的标签非零。f(x_ij) 表示的是样本i预测为j分类的概率。loss的大小完全取决于分类为正确标签那一类的概率，当所有的样本都分类正确时，loss=0，否则大于0。

2.3、softmax loss及其变种

假如log loss中的f(x_ij)的表现形式是softmax概率的形式，那么交叉熵loss就是熟知的softmax with cross-entropy loss，简称softmax loss，所以说softmax loss只是交叉熵的一个特例。

softmax loss被广泛用于分类分割等任务，且发展出了很多的变种，有针对不平衡样本问题的weighted softmax loss，  focal loss，针对蒸馏学习的soft softmax loss，促进类内更加紧凑的L-softmax Loss等一系列的改进：

2.3.1、softmax loss

softmax loss实际上是由softmax和cross-entropy loss组合而成，两者放一起数值计算更加稳定。推到过程如下：

令z是softmax层的输入，f(z)是softmax的输出，则

单个像素i的softmax loss等于cross-entropy error如下:

 

展开上式：

在caffe实现中，z即bottom blob，l(y,z)是top blob，反向传播时，就是要根据top blob diff得到bottom blob diff，所以要得到 

下面求loss对z的第k个节点的梯度

可见，传给groundtruth label节点和非groundtruth label节点的梯度是不一样的。

原始的softmax loss非常优雅，简洁，被广泛用于分类问题。它的特点就是优化类间的距离非常棒，但是优化类内距离时比较弱。

2.3.2、weighted softmax loss

假如一个二分类问题，两类的样本数目差距非常之大。如边缘检测问题，边缘像素的重要性明显比非边缘像素大的重要性要大，此时可以针对性的对样本进行加权。

w_c就是这个权重， c=0代表边缘像素，c=1代表非边缘像素，则可以令w₀=1，w₁=0.001，即加大边缘像素的权重。这个权重，还可以动态地计算让其自适应。

2.3.3、soft softmax loss

当T=1时，就是softmax的定义，当T>1，就称之为soft softmax，T越大，因为Z_k产生的概率差异就会越小。作者提出这个是为了迁移学习，生成软标签，然后将软标签和硬标签同时用于新网络的学习。

为什么这么用，当训练好一个模型之后，模型为所有的误标签都分配了很小的概率；然而实际上对于不同的错误标签，其被分配的概率仍然可能存在数个量级的悬殊差距。这个差距，在softmax中直接就被忽略了，但这其实是一部分有用的信息。

作者先利用softmax loss训练获得一个大模型，然后基于大模型的softmax输出结果获取每一类的概率，将这个概率，作为小模型训练时soft target的label。

2.3.4、Large-Margin Softmax Loss / L-Softmax loss

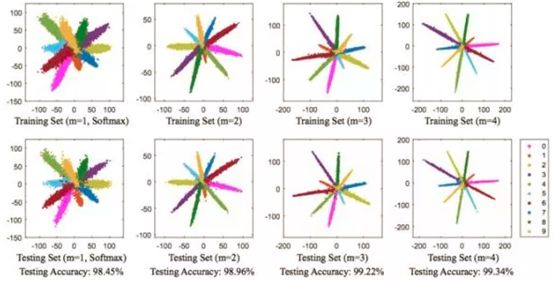
上图显示的是不同softmax loss和L-Softmax loss学习到的cnn特征分布。第一列就是softmax，第2列是L-Softmax loss在参数m取不同值时的分布。通过可视化特征，可知学习到的类间的特征是比较明显的，但是类内比较散。而large-margin softmax loss则类内更加紧凑，怎么做到的呢？

loss的定义形式:

由于 z_k 是全连接层的输出，所以可以写成形式如下:

将内积更具体的表现出来，就是：

对于二分类的情况，对于属于第1类的样本，希望：

若对它提出更高的要求？由于cos函数在0～PI区间是递减函数，将其改为：

其中m>=1，

在这个条件下，原始的softmax条件仍然得到满足。

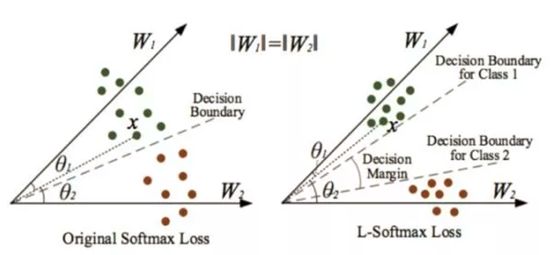
下图，如果W₁=W₂，那么满足条件2，显然需要θ1与θ2之间的差距变得更大，原来的softmax的decision boundary只有一个，而现在类别1和类别2的decision boundary不相同，这样类间的距离进一步增加，类内更近紧凑。

更具体的定义如下：

 

L-Softmax loss中，m是一个控制距离的变量，它越大训练会变得越困难，因为类内不可能无限紧凑。作者是通过一个LargeMargin全连接层+softmax loss来共同实现。

2.3.5、L2-constrained softmax loss

将学习的特征x归一化。观测到好的正面的脸，特征的L2-norm大，而特征不明显的脸，其对应的特征L2-norm小，因此，作者提出这样的约束来增强特征的区分度：

 

上面式就是将其归一化到固定值α。实际训练的时候都不需要修改代码，只需要添加L2-norm层与scale层，如下图：

 

为什么要加这个scale层？NormFace指出了直接归一化权重和特征，会导致loss不能下降。因为就算是极端情况下，多类样本，令正样本|wx|=1取最大值，负样本|wx|=-1取最小值，这时候分类概率也是

 

当类别数n=10，p=0.45；n=1000，p=0.007。当类别数增加到1000类时，正样本最大的概率还不足0.01，而反向求导的时候，梯度=1-p，会导致一直传回去很大的loss。所以，有必要在后面加上scale层。

2.4、KL散度

Kullback和Leibler定义了KL散度用于估计两个分布的相似性，定义如下；

 

D_kl是非负的，只有当p与q处处相等时，才会等于0。上式也等价于

 

其中l(p,p)是分布p的熵，而l(p,q)就是p和q的交叉熵。假如p是一个已知的分布，则熵是一个常数，此时D_kl(p|q)与l(p,q)只有一个常数的差异，两者是等价的。但是，KL散度并不是一个对称的loss，即D_kl (p|q) != D_kl (q|p)，KL散度常被用于生成式的模型。

2.5、Hinge loss

Hinge loss主要用于支持向量机中，它的称呼来源于损失的形式，定义如下：

 

如果分类正确，loss=0，如果错误则为1-f(x)，所以它是一个分段不光滑的曲线。Hinge loss被用来解SVM问题中的间距最大化问题。

2.6、Exponential loss与Logistic loss

Exponential loss是一个指数形式的loss，特点是梯度比较大，主要用于Adaboost集成学习算法中，定义如下：

 

logistic loss取了Exponential loss的对数形式，它的定义如下：

 

logistic loss 梯度相对变化更加平缓。

此外，还有sigmoid cross_entropy_loss，可以被用于多标签分类任务或者不需要创建类间竞争机制的分类任务，在Mask RCNN中就使用了sigmoid cross_entropy_loss。

 

以上涵盖了大部分常用的分类任务损失，大部分都是对数的形式，这是由信息熵的定义和参数似然估计的本质决定的。

3 回归任务损失

在回归任务中，回归的结果是一些整数或者实数，并没有先验的概率密度分布，常使用的loss是L1 loss和L2 loss。

3.1、L1 loss

Mean absolute loss(MAE)也被称为L1 Loss，是以绝对误差作为距离：

由于L1 loss具有稀疏性，为了惩罚较大的值，因此常常将其作为正则项添加到其他loss中作为约束。L1 loss的最大问题是梯度在零点不平滑，会跳过极小值点。

3.2、L2 loss

Mean Squared Loss/ Quadratic Loss(MSE loss)也被称为L2 loss，或欧氏距离，它以误差的平方和作为距离：

 

L2 loss也常常作为正则项。当预测值与目标值相差很大时, 梯度容易爆炸（因为梯度里包含了x−t）。

3.3、L1 loss与L2 loss的改进

原始的L1 loss和L2 loss都有缺陷，如L1 loss的最大问题是梯度不平滑，而L2 loss的最大问题是容易梯度爆炸，所以研究者们对其提出了很多的改进。

在faster RCNN框架中，使用了smooth L1 loss来综合L1与L2 loss的优点，定义如下:

在x比较小时，上式等价于L2 loss，保持平滑。在x比较大时，上式等价于L1 loss，可以限制数值的大小。

为了增强L2 loss对噪声(离群点)的鲁棒性，研究者提出了Huber loss，定义如下：

Huber对于离群点非常的有效，它同时结合了L1与L2的优点，不过多出来了一个delta参数需要进行训练。除此之外还有Log-Cosh Loss等损失。

从上文可以看出，L1/L2各有优劣，设计一个通用的框架同时满足L1/L2损失的优点是研究重点，有如下：

3.4、感知损失perceptual loss

对于图像风格化，图像超分辨率重建等任务来说，早期都使用了图像像素空间的L2 loss，但是L2 loss与人眼感知的图像质量并不匹配，恢复出来的图像往往细节表现不好。现在的研究中，L2 loss逐步被人眼感知loss所取代。人眼感知loss也被称为perceptual loss（感知损失），它与MSE采用图像像素进行求差的不同之处在于所计算的空间不再是图像空间。

研究者们常使用VGG等网络的特征，令φ来表示损失网络，C_j表示网络的第j层，C_jH_jW_j表示第j层的特征图的大小，感知损失的定义如下：

 

可以看出，perceptual loss与L2 loss具有同样的形式，只是计算的空间被转换到了特征空间。

4 生成对抗网络损失

生成对抗网络即Generative Adversarial Networks，简称GAN，于2014年以后兴起的无监督学习网络。原始的用于生成图片的GAN的损失函数包括了生成式模型和判别式模型两部分，如今GAN被用于各类任务，其他的各种损失也被引入，在此仅针对GAN的基本损失进行阐述。

4.1、GAN的基本损失

GAN是在生成模型和判别模型的相互博弈中进行迭代优化，它的优化目标如下：

 

从上式可以看出，包含两个部分：E_x∼pdata(x)[logD(x)]和E_z∼pz(z)[log(1−D(G(z)))]，要求最大化判别模型D对真实样本的概率估计，最小化判别模型D对生成的样本的概率估计，生成器G则要求最大化D(G(z))，即最大化判别模型对生成样本的误判，这里的loss是对数log的形式。

原始的GAN的损失使用了JS散度，两个分布之间越接近，它们的JS散度越小，但实际上这并不适合衡量生成数据分布和真实数据分布的距离，相关的分析请查阅相关文献。

4.2、-log D trick

Ian Goodfellow提出了-log D trick，使得生成器的损失不依赖于生成器G，即把生成器loss改成如下：

最小化目标存在两个严重的问题：第一是它同时要最小化生成分布与真实分布的KL散度，却又要最大化两者的JS散度，这是矛盾的会导致梯度不稳定。第二，因为KL散度不是对称的，导致此时loss不对称，对于正确样本误分和错误样本误分的惩罚是不一样的。第一种错误对应的是“生成器没能生成真实的样本”，即多样性差，惩罚微小；第二种错误对应的是“生成器生成了不真实的样本”，即准确性低，惩罚巨大。这样造成生成器生成多样性很差的样本，出现了常说的模式崩塌(collapse mode)问题。

4.3、Wasserstein GAN(简称wgan)等改进方案

wgan采用了Earth-Mover距离(EM距离)作为loss，它是在最优路径规划下的最小消耗，计算的是在联合分布γ下，样本对距离的期望值：

 

与原始的GAN的loss形式相比，wgan的生成器和判别器的loss不取log。wessertein距离相比KL散度和JS散度的优势在于：即使两个分布的支撑集没有重叠或者重叠非常少，仍然能够反映两个分布的远近。而JS散度在此情况下是常量，KL散度可能无意义。wgan有一些问题，wgan-gp改进了wgan连续性限制的条件，相关最新研究请查阅文献。

4.4、LS-GAN

LS-GAN即Least Squares Generative Adversarial Networks。它的原理部分可以一句话概括：使用了最小二乘损失函数代替了GAN的损失函数。这相当于最小化P和Q之间的Pearson卡方散度（divergence），属于f-divergence的一种，有效地缓解了GAN训练不稳定和生成图像质量差多样性不足的问题。提出者认为使用JS散度并不能拉近真实分布和生成分布之间的距离，使用最小二乘可以将图像的分布尽可能的接近决策边界，其损失函数定义如下：

以交叉熵作为损失，它的特点是会使得生成器不会再优化那些被判别器识别为真实图片的生成图片，即使这些生成图片距离判别器的决策边界仍然很远，也就是距真实数据比较远，这意味着生成器的生成图片质量并不高。而要想最小二乘损失比较小，则在混淆判别器的前提下还得让生成器把距离决策边界比较远的生成图片拉向决策边界，这就是LS-GAN的优势。

4.5、Loss-sensitive-GAN

在原始的GAN的损失函数后添加了一个约束项来直接限定GAN的建模能力，它的损失函数如下：

优化将通过最小化这个目标来得到一个“损失函数" (下文称之为L函数)。L函数在真实样本上越小越好，在生成的样本上越大越好。它是以真实样本x和生成样本的一个度量为各自L函数的目标间隔，把x和生成样本分开。好处是如果生成的样本和真实样本已经很接近，就不必要求他们的L函数有个固定间隔，因为生成的样本已经很好。这样就可以集中力量提高那些距离真实样本还很远，真实度不那么高的样本，能更合理地使用LS-GAN的建模能力，被称为“按需分配”。

关于GAN的损失优化：

 

推荐GAN论文网址：https://hollobit.github.io/All-About-the-GAN/

 

学习来源于网络：公众号 有三AI

https://mp.weixin.qq.com/s/ixYhM29-famb8lbzNYnHAg

https://mp.weixin.qq.com/s/BdSdBw7FbzswCBsEivDANw

转载于:https://www.cnblogs.com/jeshy/p/10629556.html