浅谈利用强化学习A3C玩转超级玛丽奥

前言

很早以前看过超级玛丽奥利用人工智能玩，以前感觉很高档。就写一篇吧。

github

https://github.com/yanjingke/Super-mario

什么是Actor-Critic？

Actor-Critic，其实是用了两个网络：两个网络有一个共同点，输入状态S: 一个输出策略，负责选择动作，我们把这个网络成为Actor； 一个负责计算每个动作的分数，我们把这个网络成为Critic。
大家可以形象地想象为，Actor是舞台上的舞者，Critic是台下的评委。Actor在台上跳舞，一开始舞姿并不好看，Critic根据Actor的舞姿打分。Actor通过Critic给出的分数，去学习：如果Critic给的分数高，那么Actor会调整这个动作的输出概率；相反，如果Critic给的分数低，那么就减少这个动作输出的概率。
在AC中中的Critic，估算的是V值也就是一个评分，因为在强化学习中，往往没有足够的时间让我们去和环境互动。在Critic中如果预测动作评价，假设我们用Critic网络，预估到S状态下三个动作A1，A2，A3的Q值分别为1,2,10。但在开始的时候，我们采用平均策略，于是随机到A1。于是我们用策略梯度的带权重方法更新策略，这里的权重就是Q值。于是策略会更倾向于选择A1，意味着更大概率选择A1。结果A1的概率就持续升高…
这就掉进了正数陷阱。我们明明希望A3能够获得更多的机会，最后却是A1获得最多的机会。这是为什么呢？
这是因为Q值用于是一个正数，如果权重是一个正数，那么我们相当于提高对应动作的选择的概率。权重越大，我们调整的幅度将会越大。其实当我们有足够的迭代次数，这个是不用担心这个问题的。因为总会有机会抽中到权重更大的动作，因为权重比较大，抽中一次就能提高很高的概率。

但在强化学习中，往往没有足够的时间让我们去和环境互动。这就会出现由于运气不好，使得一个很好的动作没有被采样到的情况发生。要解决这个问题，我们可以通过减去一个baseline，令到权重有正有负。而通常这个baseline，我们选取的是权重的平均值。减去平均值之后，值就变成有正有负了。

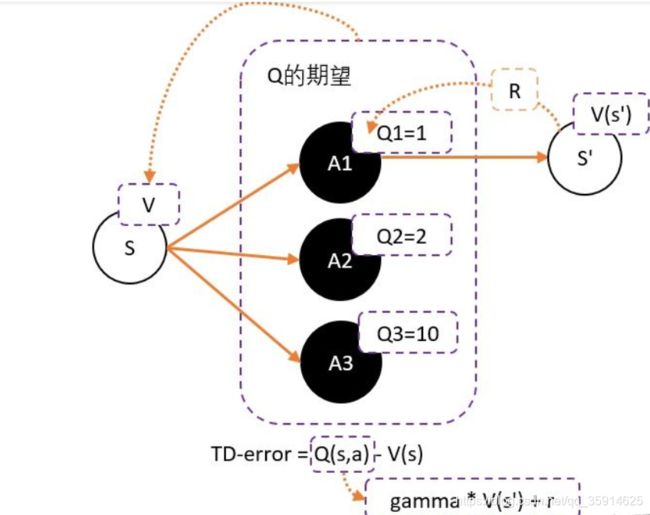
所以我们可以得到更新的权重：Q(s,a)-V(s)。然而在每次的奖励中会进行得分的衰减gamma。
总结

1、为了避免正数陷阱，我们希望Actor的更新权重有正有负。因此，我们把Q值减去他们的均值V。有：Q(s,a)-V(s)

2、为了避免需要预估V值和Q值，我们希望把Q和V统一；由于Q(s,a) = gamma * V(s’) + r - V(s)。所以我们得到TD-error公式： TD-error = gamma * V(s’) + r - V(s)

A3C算法

在A3C中有一个公共的神经网络模型，这个神经网络包括Actor网络和Critic网络两部分的功能这样加快了速度。下面有n个worker线程，每个线程里有和公共的神经网络一样的网络结构，每个线程会独立的和环境进行交互得到经验数据，这些线程之间互不干扰，独立运行。

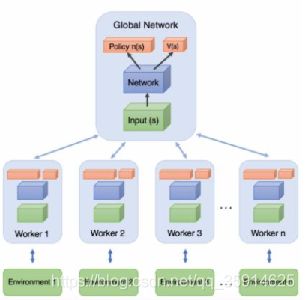
它是怎么实现公共网络的啦？
在A3C中需要解决的问题：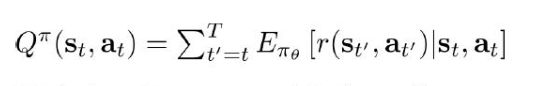

由于智能体在与环境交互过程中有大量的随机性，所以算的是期望，为了计算A，现在出现了Q和V，那我得训练俩网络了，
来个近似让问题简单些吧：

是不是不用训练两个网络啦？对

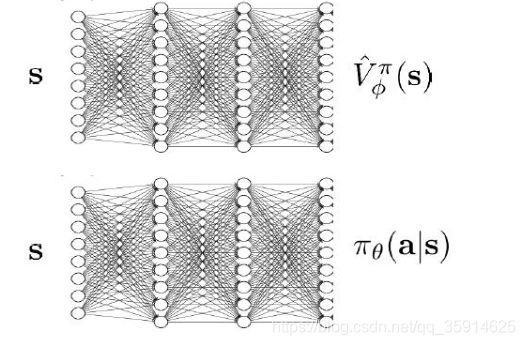
它俩好像都是根据状态来预测结果：

class ActorCritic(nn.Module):
    def __init__(self, num_inputs, num_actions):
        super(ActorCritic, self).__init__()
        self.conv1 = nn.Conv2d(num_inputs, 32, 3, stride=2, padding=1)
        self.conv2 = nn.Conv2d(32, 32, 3, stride=2, padding=1)
        self.conv3 = nn.Conv2d(32, 32, 3, stride=2, padding=1)
        self.conv4 = nn.Conv2d(32, 32, 3, stride=2, padding=1)
        self.lstm = nn.LSTMCell(32 * 6 * 6, 512)
        self.critic_linear = nn.Linear(512, 1)
        self.actor_linear = nn.Linear(512, num_actions)
        self._initialize_weights()

    def _initialize_weights(self):
        for module in self.modules():
            if isinstance(module, nn.Conv2d) or isinstance(module, nn.Linear):
                nn.init.xavier_uniform_(module.weight)
                # nn.init.kaiming_uniform_(module.weight)
                nn.init.constant_(module.bias, 0)
            elif isinstance(module, nn.LSTMCell):
                nn.init.constant_(module.bias_ih, 0)
                nn.init.constant_(module.bias_hh, 0)

    def forward(self, x, hx, cx):
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        x = F.relu(self.conv3(x))
        x = F.relu(self.conv4(x))
        # print( (hx, cx))
        hx, cx = self.lstm(x.view(x.size(0), -1), (hx, cx))
        return self.actor_linear(hx), self.critic_linear(hx), hx, cx#隐层和记忆单元

AC整体流程：
1.获取数据： （不断与环境交互，通过策略 ）
2.前向传播计算：

3.计算梯度：

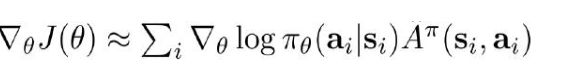
4.更新参数：

def local_train(index, opt, global_model, optimizer, save=False):
    torch.manual_seed(123 + index)
    if save:
        start_time = timeit.default_timer()
    writer = SummaryWriter(opt.log_path)
    env, num_states, num_actions = create_train_env(opt.world, opt.stage, opt.action_type)#单独玩
    local_model = ActorCritic(num_states, num_actions)
    if opt.use_gpu:
        local_model.cuda()
    local_model.train()
    state = torch.from_numpy(env.reset())
    if opt.use_gpu:
        state = state.cuda()
    done = True
    curr_step = 0
    curr_episode = 0
    while True:
        if save:
            if curr_episode % opt.save_interval == 0 and curr_episode > 0:
                torch.save(global_model.state_dict(),
                           "{}/a3c_super_mario_bros_{}_{}".format(opt.saved_path, opt.world, opt.stage))
            print("Process {}. Episode {}".format(index, curr_episode))
        curr_episode += 1
        local_model.load_state_dict(global_model.state_dict())
        if done:
            h_0 = torch.zeros((1, 512), dtype=torch.float)
            c_0 = torch.zeros((1, 512), dtype=torch.float)
        else:
            h_0 = h_0.detach()
            c_0 = c_0.detach()
        if opt.use_gpu:
            h_0 = h_0.cuda()
            c_0 = c_0.cuda()

        log_policies = []
        values = []
        rewards = []
        entropies = []

        for _ in range(opt.num_local_steps):
            curr_step += 1
            logits, value, h_0, c_0 = local_model(state, h_0, c_0)#return self.actor_linear(hx), self.critic_linear(hx), hx, cx#隐层和记忆单元
            policy = F.softmax(logits, dim=1)
            log_policy = F.log_softmax(logits, dim=1)
            entropy = -(policy * log_policy).sum(1, keepdim=True)#计算当前熵值

            #进行分布采样
            m = Categorical(policy)#采样
            action = m.sample().item()

            state, reward, done, _ = env.step(action)
            # env.render()
            state = torch.from_numpy(state)
            if opt.use_gpu:
                state = state.cuda()
            if curr_step > opt.num_global_steps:
                done = True

            if done:
                curr_step = 0
                state = torch.from_numpy(env.reset())
                if opt.use_gpu:
                    state = state.cuda()

            values.append(value)
            log_policies.append(log_policy[0, action])
            rewards.append(reward)
            entropies.append(entropy)

            if done:
                break

        R = torch.zeros((1, 1), dtype=torch.float)
        if opt.use_gpu:
            R = R.cuda()
        if not done:
            _, R, _, _ = local_model(state, h_0, c_0)#这个R相当于最后一次的V值，第二个返回值是critic网络的

        gae = torch.zeros((1, 1), dtype=torch.float)#额外的处理，为了减小variance
        if opt.use_gpu:
            gae = gae.cuda()
        actor_loss = 0
        critic_loss = 0
        entropy_loss = 0
        next_value = R

        for value, log_policy, reward, entropy in list(zip(values, log_policies, rewards, entropies))[::-1]:
            gae = gae * opt.gamma * opt.tau
            gae = gae + reward + opt.gamma * next_value.detach() - value.detach()#Generalized Advantage Estimator 带权重的折扣项
            next_value = value
            actor_loss = actor_loss + log_policy * gae
            R = R * opt.gamma + reward
            critic_loss = critic_loss + (R - value) ** 2 / 2
            entropy_loss = entropy_loss + entropy

        total_loss = -actor_loss + critic_loss - opt.beta * entropy_loss
        writer.add_scalar("Train_{}/Loss".format(index), total_loss, curr_episode)
        optimizer.zero_grad()
        total_loss.backward()

        for local_param, global_param in zip(local_model.parameters(), global_model.parameters()):
            if global_param.grad is not None:
                break
            global_param._grad = local_param.grad

        optimizer.step()

        if curr_episode == int(opt.num_global_steps / opt.num_local_steps):
            print("Training process {} terminated".format(index))
            if save:
                end_time = timeit.default_timer()
                print('The code runs for %.2f s ' % (end_time - start_time))
            return

loss值计算

策略损失（Policy）: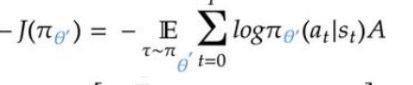
（起决策的网络）
Value网络损失：
（预期与实际的差异）
熵：（熵越大表示各种行为可能性都能有一些，别太绝对）
整体损失函数：

  for value, log_policy, reward, entropy in list(zip(values, log_policies, rewards, entropies))[::-1]:
            gae = gae * opt.gamma * opt.tau
            gae = gae + reward + opt.gamma * next_value.detach() - value.detach()#Generalized Advantage Estimator 带权重的折扣项
            next_value = value
            actor_loss = actor_loss + log_policy * gae
            R = R * opt.gamma + reward
            critic_loss = critic_loss + (R - value) ** 2 / 2
            entropy_loss = entropy_loss + entropy

        total_loss = -actor_loss + critic_loss - opt.beta * entropy_loss
        writer.add_scalar("Train_{}/Loss".format(index), total_loss, curr_episode)
        optimizer.zero_grad()
        total_loss.backward()