强化学习相关概念梳理

强化学习相关概念梳理

强化学习概念特别多，且涉及大量数学知识，此文章旨在梳理一些基本概念，如有错误，欢迎指正！

目录

• 强化学习的基本组成元素
• 马尔科夫决策过程(MDP)
• 贝尔曼方程
  
  

正文

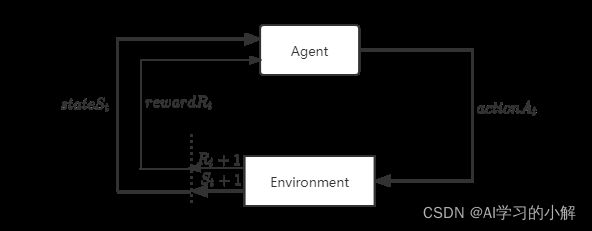
1.强化学习的基本组成元素

为了便于理解，举一个爷青回的例子：超级玛丽，相信大家都玩过！

• agent（智能体）：强化学习的本体，作为学习者或决策者存在。例如上图中的马里奥。
• environment（环境）：agent以外的一切，主要指状态。例如上图的马里奥游戏环境。
• state（状态）：记为S，表示environment的数据，例如马里奥游戏的一帧。状态集是environment中所有可能的state。
• action（动作）：记为A，agent所能执行的操作。例如图中马里奥智能执行up，left，right。动作集是agent所能做出的所有动作。
• policy（策略）：记为π，从state到action的映射，agent基于某种state选择某种action的过程。根据观测到的state，做出决策，控制agent运动。公式如下：

$$\pi (a|s)=P(A=a|S=s)$$
实际上$\pi (a|s)$ 是一个 概率密度函数，即：给定状态s，做出动作a的概率密度
eg:
             $\pi (left|s)=0.2$ , 20%的可能性朝左走
             $\pi (right|s)=0.1$, 10%的可能性朝右走
             $\pi (up|s)=0.7$, 70%的可能性朝上走
在state S = s时，agent的动作是随机的。

• reward（奖励）：记为R，agent在执行一个动作后，获得的正负奖励信号。

eg:如上图马里奥游戏中：
           收集到金币：R = + 1
           赢得游戏：R = + 10000
           碰到敌人（game over）：R = - 10000
           无事发生：R = 0
这些奖励都是根据实际情况认为设计的。

• state transition（状态转移）：

action

old_state

new_state

$$p(s^{{}^{\prime }},r|s,a)=P(S_{t+1}=s^{{}^{\prime }},R_{t+1}=r|S_t=s,A_t=a)$$
从式子中可以看出t+1时刻的状态s’,和奖励r是由t时刻的状态s和执行的动作a决定的。是一个 条件概率密度函数
注意：
  1.状态转移可以是确定的，也可以是随机的，通常都是随机的。例如多臂赌博机中就是确定的，马里奥游戏中就是不确定的。
  2.状态转移的随机性来源于环境内部。例如马里奥游戏中，当前状态执行一个动作后，下一个状态是由游戏内部机制所决定的。

• rerurn（未来的累计奖励）：记为U（也有的记为G），未来所有时刻的总回报。公式如下：

$$U_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+{\gamma }^3{R}_{t+4}+...$$
其中，$\gamma$为折扣率，$\gamma \in [0,1]$，因为时间越久远的回报对当前的回报价值越低，就比如说，你今天掉了一百块钱，可能会影响你中午的伙食（钱丢了，少吃一点），但对100天后的你来说，之前丢的一百块钱并不算什么。

强化学习的目标：获得的累计奖励要尽可能高！！！

2.马尔科夫决策过程(MDP)

• MDP是在环境中模拟智能体的随机性策略（policy）与回报的数学模型，且环境的状态具有马尔可夫性质。
• 马尔可夫性质：也叫后无效性，指在时间步t+1时，环境的反馈仅取决于上一时间步t的状态s和动作a，与时间步t-1及t-1步之前的时间步都没有关联性。马尔科夫性是一种为了简化问题而做的假设。

具体过程如下图：

马尔科夫过程可表示为一个五元组：
$$MDP(S,A,P,R,\gamma )$$
其中S为状态，A为动作，P为状态转移概率，R为奖励，$\gamma$为折扣率

基本流程如下：

Created with Raphaël 2.3.0 开始 初始化:S,P,R,γ ,π，t = 0 继续条件：t

其中，T为终止时间步数。
MDP会产生一个状态-动作-奖励序列：
$s_0,a_0,r_1,s_1,a_1,r_2,s_2,a_2,r_3,\dots ,s_t,a_t,r_{t+1},\dots ,s_{T-1},a_{T-1},r_T,s_T$
累计奖励为：$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+{\gamma }^3{R}_{t+4}+...$

目标：使累计奖励最大。

下面举一个例子将上述l两部分概念捋一遍：

机器人在如下表格中走路，障碍为（2,2）的格子，机器人碰到墙或障碍物会保持不动。机器人初始状态为格子（1,3），若机器人走到格子（3,4），则过程结束。

• 状态集合：由11个状态构成，分别为除障碍物外的每一个格子
  $S=\left\{(1,1),(1,2),...,(3,4)\right\}$
• 动作集合：由4个动作组成，每个移动方向为一个动作
  $A=\left\{up,down,left,right\right\}$
• 状态转移概率：由于机器人轮子打滑等原因，即便给出的动作命令是down，机器人也会以0.1的概率分别执行left或right，比如当机器人处在状态(1, 3)，被要求执行动作down时，我们有：
  $P_{(1,3),down}((2,3))=0.8$  在状态(1, 3)执行动作down时，转移到状态(2, 3)的概率为0.8
  $P_{(1,3),left}((1,2))=0.1$
  $P_{(1,3),right}((1,4))=0.1$
• 奖励函数：
  $R((2,3),down,(3,3))=0$ 在状态(2, 3)执行动作down，到达状态(3, 3),所得到的奖励为0
  $R((3,3),left,(3,4))=1$  在状态(3, 3)执行动作left，到达状态(3, 4),所得到奖励为1，因为到达了终点
• 折扣因子：
  $\gamma \in [0,1]$
• MDP序列：
  $s_0,a_0,r_1,s_1,a_1,r_2,s_2,a_2,r_3,\dots ,s_{T-1},a_{T-1},r_T,s_T$
• 累计奖励：
  $G_0=r_1+\gamma r_2+{\gamma }^2{r}_3+{\gamma }^3{r}_4+...+{\gamma }^{T-1}{r}_T$

3.贝尔曼方程

• Value Function（价值函数）：定义如下：

$$V_{\pi }(s)=E_{\pi }[G_t|S_t=s]$$
其中，$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+{\gamma }^3{R}_{t+4}+...$
解释：在当前状态已知的情况改下，采取策略π，所获得的累计奖励的期望。为什么是期望呢？
如上图的回溯图，当状态$S_t=s$时，根据策略函数$\pi (a|s)$，会执行动作$a_1,a_2,a_3$中的一个（由于策略函数π是个概率密度函数，所以这三个动作都有被执行的可能）；在选择执行哪个动作之后，再根据状态转移函数$p(s^{{}^{\prime }},r|s,a)$得到下一个状态$s^{{}^{\prime }}$,并获得奖励$r_t$,由于状态转移函数也是概率密度函数，此过程也是随机的，$s_1,s_2,s_3$都有被执行的可能。由于以上这些随机性，用期望的形式才能更好的表示价值函数。

价值函数还可以化简如下:

$V_{\pi }(s)=E_{\pi }[G_t|S_t=s]$
      $=E_{\pi }[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+{\gamma }^3{R}_{t+4}+...|S_t=s]$
      $=E_{\pi }[R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+{\gamma }^2{R}_{t+4}+...)|S_t=s]$
      $=E_{\pi }[R_{t+1}+\gamma G_{t+1}|S_t=s]$
      $={\sum }_a^{}\pi \left(a|s\right){\sum }_{s^{{}^{\prime }}}{\sum }_r^{}p\left(s^{{}^{\prime }},r\mid s,a\right)[r+\gamma E_{\pi }\left[G_{t+1}\mid S_{t+1}=s^{{}^{\prime }}\right]]$  离散随机变量的期望定义
      $={\sum }_a^{}\pi \left(a|s\right){\sum }_{s^{{}^{\prime }},r}p\left(s^{{}^{\prime }},r\mid s,a\right)[r+\gamma V_{\pi }\left(s^{{}^{\prime }}\right)]$

价值函数的意义：

说通俗一点就是：判断当前的局势好不好，比如游戏中是快赢了还是快输了，$V_{\pi }\left(s\right)$越大代表局势越好。

• Action-value Function（动作价值函数）：定义如下：

$$Q_{\pi }(s,a)=E_{\pi }[G_t|S_t=s,A_t=a]$$
解释：在当前状态已知的情况改下，采取策略π并执行动作a之后，所获得的累计奖励的期望。

动作价值函数化简如下：

$Q_{\pi }(s,a)=E_{\pi }[G_t|S_t=s,A_t=a]$
      $=E_{\pi }[R_{t+1}+\gamma G_{t+1}|S_t=s,A_t=a]$
      $={\sum }_{s^{{}^{\prime }},r}p\left(s^{{}^{\prime }},r\mid s,a\right)[r+\gamma V_{\pi }\left(s^{{}^{\prime }}\right)]（1）$

动作价值函数的意义：

$Q_{\pi }\left(s,a\right)$对当前状态s下，通过策略执行的动作a进行评估（打分），$Q_{\pi }\left(s,a\right)$越大说明当前执行的动作a越好。

• Value Function 和 Action-value Function二者之间的关系：
  很多资料都是从公式角度出发，一步一步推导出二者关系，对于数学底子薄弱的同学可能很难理解，所以我将从回溯图的角度直观的介绍二者之间的关系。

回溯图

如上图所示，状态价值函数$V_{\pi }\left(s\right)$只要知道当前状态和策略就可以进行计算之后的累计回报，而动作价值函数$Q_{\pi }\left(s,a\right)$还需要知道确切的选择动作，才能计算之后的累计回报。二者之间仅仅差了一个动作的选择，而动作的选择靠的就是策略$\pi (a|s)$。所以很明显的可以得到下式：
$$V_{\pi }=\sum _{a\in A}\pi (a|s)\cdot Q_{\pi }(s,a)$$
$$Q_{\pi }(s,a)=\sum _{s^{{}^{\prime }},r}p\left(s^{{}^{\prime }},r\mid s,a\right)[r+\gamma V_{\pi }\left(s^{{}^{\prime }}\right)]（1）$$

• Optimal Value Function（最优价值函数）：定义如下：

$$V_{\ast }(s)=ma{x}_{\pi }{V}_{\pi }(s)$$
解释：所有策略$\pi$中，所计算出来的$V_{\pi }(s)$中的最大值，即为$V_{\ast }(s)$，此时策略$\pi$就是最好的策略。也就是说，无论采取任何策略$\pi$，所计算出来的$V_{\pi }(s)$都不可能大于$V_{\ast }(s)$。

最优价值函数化简如下：

$V_{\ast }(s)=ma{x}_{\pi }{V}_{\pi }(s)$
      $=max{E}_{\pi }[R_{t+1}+\gamma G_{t+1}|S_t=s]$
      $=max{\sum }_a^{}\pi \left(a|s\right){\sum }_{s^{{}^{\prime }},r}p\left(s^{{}^{\prime }},r\mid s,a\right)[r+\gamma V_{\pi }\left(s^{{}^{\prime }}\right)]$ 取最好的策略$\pi$
      $=ma{x}_a{\sum }_{s^{{}^{\prime }},r}p\left(s^{{}^{\prime }},r\mid s,a\right)[r+\gamma V_{\ast }\left(s^{{}^{\prime }}\right)]$

• Optimal Action-value Function（最优动作价值函数）：定义如下：

$$Q_{\ast }(s,a)=ma{x}_{\pi }{Q}_{\pi }(s,a)$$
解释：无论使用什么策略$\pi$，所计算出最大的$Q_{\pi }(s,a)$。

最优动作价值函数化简如下：

$Q_{\ast }(s,a)=ma{x}_{\pi }{Q}_{\pi }(s,a)$
      $=ma{x}_{\pi }{E}_{\pi }[G_t|S_t=s,A_t=a]$
      $={\sum }_{s^{{}^{\prime }},r}p\left(s^{{}^{\prime }},r\mid s,a\right)[r+\gamma ma{x}_{a^{\prime }}{Q}_{\ast }\left(s^{{}^{\prime }},a^{{}^{\prime }}\right)]$