TensoRF-张量辐射场论文笔记

TensoRF-张量辐射场论文笔记

TensoRF: Tensorial Radiance Fields 是2022 年ECCV上的论文

论文地址：https://arxiv.org/abs/2203.09517
源码地址：https://github.com/apchenstu/TensoRF

论文讲解视频：B站视频 TensoRF-张量辐射场简介

代码讲解视频：B站视频 TensoRF-源码简介

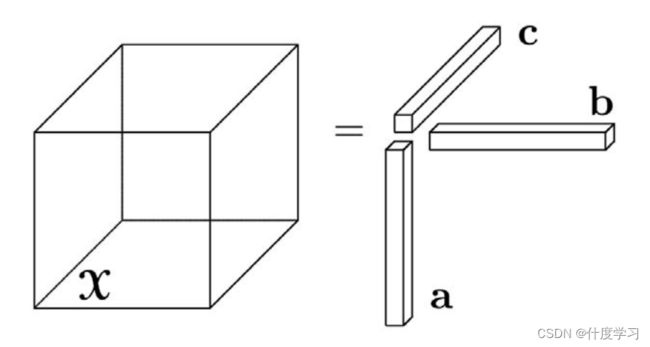
张量辐射场是一种新颖的建模和重建辐射场的方法。跟NeRF使用多层感知机隐式建模场景表达的方式不同，TensoRF将场景建模为一个四维的张量，张量中的每一项代表了一个体素，体素内包含了体积密度和多维的特征信息

论文的中心思想是使用张量分解技术，将4D张量分解成多个低秩的张量分量，以小见大

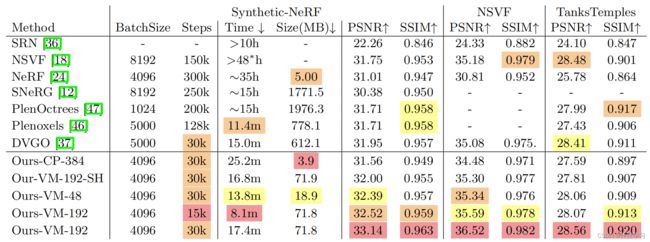
从上图中可以看出，张量辐射场可以达到：

1. 更好的质量
2. 更快的速度
3. 更小的模型体积

张量辐射场除了渲染质量更好之外，与同时期使用体素方式的研究相比占用更少的内存使用

张量辐射场在30分钟内就可以完成重建，并且模型的大小小于4M，这比NeRF更快，以及更小巧

使用VM分解方式的可以达到10分钟的时间，以及更好的质量，模型大小小于75M

TensoRF是第一个从张量的角度来看待辐射场建模，并提出了辐射场重建作为一个低秩张量重建的问题

---

张量分解

论文中的使用的张量分解技术是通用的，论文中使用了CP分解和VM分解，当然也可以尝试使用其他的张量分解方式

通过CP/VM分解，紧凑地编码了体素网格中的空间变化的特征
体积密度和视角相关的颜色值可以从特征中解码出来

最常见的两种张量分解方式

1. Tucker decomposition
2. CP decomposition

这两种分解方法可以看成是张量奇异值分解的推广

CP分解可以认为是一种特殊的Tucker分解

在理解CP分解之前需要知道两个向量的知识

1. 向量外积
2. Rank-one 秩一张量

向量外积

$$c=\mathbf{a}\otimes \mathbf{b}=\mathbf{a}{\mathbf{b}}^{\top }=\left[\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_m\end{array}\right]\left[\begin{array}{llll}{b}_1& b_2& \cdots & b_n\end{array}\right]=\left[\begin{array}{cccc}{a}_1{b}_1& a_1{b}_2& \dots & a_1{b}_n\\ a_2{b}_1& a_2{b}_2& \dots & a_2{b}_n\\ ⋮& ⋮& \ddots & ⋮\\ a_m{b}_1& a_m{b}_2& \dots & a_m{b}_n\end{array}\right]$$

在这里的a b 两个向量的长度并无要求

同理，在后面的3D张量的分解中 a b c 三个向量的长度也没有要求（其实就是跟3D张量的各个维度的长度一样）

注意：向量的外积和向量的叉乘并不是一个意思

Rank-one tensor （秩一张量）

如果一个张量可以写成N个向量的外积，这个张量就是秩一张量
$$\mathbf{X}\in {\mathbb{R}}^{I_1\times I_2\times \cdots \times I_N}$$

$$\mathcal{X}={\mathbf{a}}^{(1)}\circ {\mathbf{a}}^{(2)}\circ \cdots \circ {\mathbf{a}}^{(N)}$$

同时，张量中的每一个元素为：

$$x_{i_1{i}_2\cdots i_N}=a_{i_1}^{(1)}{a}_{i_2}^{(2)}\cdots a_{i_N}^{(N)}\text{ for all }1\le i_n\le I_n$$

CP分解

cp分解是将其变成一些向量外积的和
更细致的说，cp分解是将其分解为秩一张量之和

多个秩一张量的和，表达式：

$$\mathbf{X}\approx \sum _{r=1}^R{\mathbf{a}}_r\circ {\mathbf{b}}_r\circ {\mathbf{c}}_r$$

这里补充一个内容，张量的秩的概念，张量的秩表示的意义跟矩阵的秩差不多
矩阵的秩是其行秩和列秩中的最小值
张量的值就是将其分解成秩一张量和的那个最小的 张量的数量，就是上面公式中 R的数量的最小值

CP分解 与 SVD

CP分解可以看成是SVD分解在张量上的推广

从张量分解成向量的外积，这里反向思考SVD分解

假设A矩阵可以分解成多个矩阵的加和
其中每一个矩阵的构成方式如下：
这里以第一个为例，第一个子矩阵就是U矩阵中的第一个向量和V矩阵中的第一个向量的外积，这两个向量的外积得到的矩阵，其大小就是与A矩阵相同的，以此类推还有第二个，第三个矩阵。。。
Sigma矩阵中的奇异值（主对角线上的值），就认为是这些子矩阵的加权系数

那么以这种视角看待SVD分解，SVD分解和CP分解的形式基本上统一的

---

VM分解

在论文中，主要介绍的内容是VM分解方式，VM分解方式与CP分解相似

VM的含义是 Vector-Matric 向量和矩阵的意思

$$\mathcal{T}=\sum _{r=1}^{R_1}{\mathbf{v}}_r^1\circ {\mathbf{M}}_r^{2,3}+\sum _{r=1}^{R_2}{\mathbf{v}}_r^2\circ {\mathbf{M}}_r^{1,3}+\sum _{r=1}^{R_3}{\mathbf{v}}_r^3\circ {\mathbf{M}}_r^{1,2}$$

上面是论文中的VM分解公式
相比于CP分解，这里有三项内容的加和，每一项有各自的组件数量R1，R2，R3，这三个值可以不同

但是在后续的内容中，认为这三个值可以设置成相同的值，因为这三项就是代表了三队向量和空间的关系，一个简单的想法便是，它们在空间中的贡献是相同的

第一项中的v可以假设其是x轴方向的向量，那么M便是yz平面的矩阵，以此类推后面两项。

---

辐射场

以上是张量分解的定义
完成了张量分解之后，下一步便是将张量中的具体的值与场景中的体积密度，表面特征建立联系

$$\sigma ,c={\mathcal{G}}_{\sigma }(\mathbf{x}),S\left({\mathcal{G}}_c(\mathbf{x}),d\right)$$

上式是论文中给出的定义公式

体积密度的详细的公式如下：

$${\mathcal{G}}_{\sigma }=\sum _{r=1}^{R_{\sigma }}{\mathbf{v}}_{\sigma ,r}^X\circ {\mathbf{M}}_{\sigma ,r}^{YZ}+{\mathbf{v}}_{\sigma ,r}^Y\circ {\mathbf{M}}_{\sigma ,r}^{XZ}+{\mathbf{v}}_{\sigma ,r}^Z\circ {\mathbf{M}}_{\sigma ,r}^{XY}=\sum _{r=1}^{R_{\sigma }}\sum _{m\in XYZ}{\mathcal{A}}_{\sigma ,r}^m$$

sigma的定义基本就是VM的公式，体积密度其本身就是一个3D的张量

表面特征的详细公式如下：

$$\begin{array}{rl}{\mathcal{G}}_c& =\sum _{r=1}^{R_c}{\mathbf{v}}_{c,r}^X\circ {\mathbf{M}}_{c,r}^{YZ}\circ {\mathbf{b}}_{3r-2}+{\mathbf{v}}_{c,r}^Y\circ {\mathbf{M}}_{c,r}^{XZ}\circ {\mathbf{b}}_{3r-1}+{\mathbf{v}}_{c,r}^Z\circ {\mathbf{M}}_{c,r}^{XY}\circ {\mathbf{b}}_{3r}\\ & =\sum _{r=1}^{R_c}{\mathcal{A}}_{c,r}^X\circ {\mathbf{b}}_{3r-2}+{\mathcal{A}}_{c,r}^Y\circ {\mathbf{b}}_{3r-1}+{\mathcal{A}}_{c,r}^Z\circ {\mathbf{b}}_{3r}\end{array}$$
表面特征是一个4D的张量，在空间XYZ的三维基础上，多了一个特征维度（这个值在代码中式27）
上面中的b向量代表的就是从XYZ空间上的值向第四维度的转换 （v M b，这三个内容合起来是4D张量）

---

模型

这里与NeRF不同的就是如何计算Sigma和RGB的中间那个区域，其他的部分，如体渲染，最后Loss的计算都是相同的

---

实验数据

上面这张图是论文中的实验对比
可以看出，TensoRF在训练时间，质量，模型大小多个维度的对比上，都有很大的提升