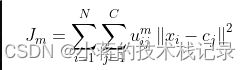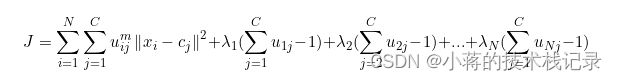2022年11月30日 Fuzzy C-Means学习笔记
Fuzzy C-Means 模糊c均值聚类,它的一大优势就是引入了一个隶属度的概念,没有对样本进行非黑即白的分类,而是分类的时候乘上隶属度,直白点说就是他和某个中心有多像,到底是40%像还是70%像。
参考:在众多模糊聚类算法中,模糊C-均值( FCM) 算法应用最广泛且较成功,它通过优化目标函数得到每个样本点对所有类中心的隶属度,从而决定样本点的类属以达到自动对样本数据进行分类的目的。
目标函数
隶属度为uij,表示第i个样本对第j类的隶属度,其中每个数据xi对于所有类别的隶属度和要为1。uij所有值求和要为1。m为聚类的簇数。xi表示第i个样本,cj表示第j个聚类中心
最小化目标函数,先将uij所有值求和要为1作为约束条件利用拉格朗日数乘法引入
再分别对uij,cj求偏导令导数等于0解得
利用这个式子进行迭代,就能得到最小化的目标函数。迭代的方式有两种,一种是设置迭代次数,另一种是设置误差阈值,当误差小于某个值的时候停止迭代。
具体步骤如下:
初始化聚类中心或隶属度举证
利用公式,不断更新隶属度矩阵和聚类中心
满足条件后停止迭代,输出聚类结果。
iris.data数据下载
python代码实现
#!/usr/bin/python3
# -*- coding: utf-8 -*-
'''
@Date : 2019/9/11
@Author : Rezero
'''
import numpy as np
import pandas as pd
def loadData(datapath):
data = pd.read_csv(datapath, sep=',', header=None)
data = data.sample(frac=1.0) # 打乱数据顺序
dataX = data.iloc[:, :-1].values # 特征
labels = data.iloc[:, -1].values # 标签
# 将标签类别用 0, 1, 2表示
labels[np.where(labels == "Iris-setosa")] = 0
labels[np.where(labels == "Iris-versicolor")] = 1
labels[np.where(labels == "Iris-virginica")] = 2
return dataX, labels
def initialize_U(samples, classes):
U = np.random.rand(samples, classes) # 先生成随机矩阵
sumU = 1 / np.sum(U, axis=1) # 求每行的和
U = np.multiply(U.T, sumU) # 使隶属度矩阵每一行和为1
return U.T
# 计算样本和簇中心的距离,这里使用欧氏距离
def distance(X, centroid):
return np.sqrt(np.sum((X-centroid)**2, axis=1))
def computeU(X, centroids, m=2):
sampleNumber = X.shape[0] # 样本数
classes = len(centroids)
U = np.zeros((sampleNumber, classes))
# 更新隶属度矩阵
for i in range(classes):
for k in range(classes):
U[:, i] += (distance(X, centroids[i]) / distance(X, centroids[k])) ** (2 / (m - 1))
U = 1 / U
return U
def ajustCentroid(centroids, U, labels):
newCentroids = [[], [], []]
curr = np.argmax(U, axis=1) # 当前中心顺序得到的标签
for i in range(len(centroids)):
index = np.where(curr == i) # 建立中心和类别的映射
trueLabel = list(labels[index]) # 获取labels[index]出现次数最多的元素,就是真实类别
trueLabel = max(set(trueLabel), key=trueLabel.count)
newCentroids[trueLabel] = centroids[i]
return newCentroids
def cluster(data, labels, m, classes, EPS):
"""
:param data: 数据集
:param m: 模糊系数(fuzziness coefficient)
:param classes: 类别数
:return: 聚类中心
"""
sampleNumber = data.shape[0] # 样本数
cNumber = data.shape[1] # 特征数
U = initialize_U(sampleNumber, classes) # 初始化隶属度矩阵
U_old = np.zeros((sampleNumber, classes))
while True:
centroids = []
# 更新簇中心
for i in range(classes):
centroid = np.dot(U[:, i]**m, data) / (np.sum(U[:, i]**m))
centroids.append(centroid)
U_old = U.copy()
U = computeU(data, centroids, m) # 计算新的隶属度矩阵
if np.max(np.abs(U - U_old)) < EPS:
# 这里的类别和数据标签并不是一一对应的, 调整使得第i个中心表示第i类
centroids = ajustCentroid(centroids, U, labels)
return centroids, U
# 预测所属的类别
def predict(X, centroids):
labels = np.zeros(X.shape[0])
U = computeU(X, centroids) # 计算隶属度矩阵
labels = np.argmax(U, axis=1) # 找到隶属度矩阵中每行的最大值,即该样本最大可能所属类别
return labels
def main():
datapath = "iris.data"
dataX, labels = loadData(datapath) # 读取数据
# 划分训练集和测试集
ratio = 0.6 # 训练集的比例
trainLength = int(dataX.shape[0] * ratio) # 训练集长度
trainX = dataX[:trainLength, :]
trainLabels = labels[:trainLength]
testX = dataX[trainLength:, :]
testLabels = labels[trainLength:]
EPS = 1e-6 # 停止误差条件
m = 2 # 模糊因子
classes = 3 # 类别数
# 得到各类别的中心
centroids, U = cluster(trainX, trainLabels, m, classes, EPS)
trainLabels_prediction = predict(trainX, centroids)
testLabels_prediction = predict(testX, centroids)
train_error = 1 - np.sum(np.abs(trainLabels_prediction - trainLabels)) / trainLength
test_error = 1 - np.sum(np.abs(testLabels_prediction - testLabels)) / (dataX.shape[0] - trainLength)
print("Clustering on traintset is %.2f%%" % (train_error*100))
print("Clustering on testset is %.2f%%" % (test_error*100))
if __name__ == "__main__":
main()
另一个代码
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Wed Mar 27 10:51:45 2019
模糊c聚类:https://blog.csdn.net/lyxleft/article/details/88964494
@author: youxinlin
"""
import copy
import math
import random
import time
global MAX # 用于初始化隶属度矩阵U
MAX = 10000.0
global Epsilon # 结束条件
Epsilon = 0.0000001
def print_matrix(list):
"""
以可重复的方式打印矩阵
"""
for i in range(0, len(list)):
print(list[i])
def initialize_U(data, cluster_number):
"""
这个函数是隶属度矩阵U的每行加起来都为1. 此处需要一个全局变量MAX.
"""
global MAX
U = []
for i in range(0, len(data)):
current = []
rand_sum = 0.0
for j in range(0, cluster_number):
dummy = random.randint(1, int(MAX))
current.append(dummy)
rand_sum += dummy
for j in range(0, cluster_number):
current[j] = current[j] / rand_sum
U.append(current)
return U
def distance(point, center):
"""
该函数计算2点之间的距离(作为列表)。我们指欧几里德距离。闵可夫斯基距离
"""
if len(point) != len(center):
return -1
dummy = 0.0
for i in range(0, len(point)):
dummy += abs(point[i] - center[i]) ** 2
return math.sqrt(dummy)
def end_conditon(U, U_old):
"""
结束条件。当U矩阵随着连续迭代停止变化时,触发结束
"""
global Epsilon
for i in range(0, len(U)):
for j in range(0, len(U[0])):
if abs(U[i][j] - U_old[i][j]) > Epsilon:
return False
return True
def normalise_U(U):
"""
在聚类结束时使U模糊化。每个样本的隶属度最大的为1,其余为0
"""
for i in range(0, len(U)):
maximum = max(U[i])
for j in range(0, len(U[0])):
if U[i][j] != maximum:
U[i][j] = 0
else:
U[i][j] = 1
return U
def fuzzy(data, cluster_number, m):
"""
这是主函数,它将计算所需的聚类中心,并返回最终的归一化隶属矩阵U.
输入参数:簇数(cluster_number)、隶属度的因子(m)的最佳取值范围为[1.5,2.5]
"""
# 初始化隶属度矩阵U
U = initialize_U(data, cluster_number)
# print_matrix(U)
# 循环更新U
while (True):
# 创建它的副本,以检查结束条件
U_old = copy.deepcopy(U)
# 计算聚类中心
C = []
for j in range(0, cluster_number):
current_cluster_center = []
for i in range(0, len(data[0])):
dummy_sum_num = 0.0
dummy_sum_dum = 0.0
for k in range(0, len(data)):
# 分子
dummy_sum_num += (U[k][j] ** m) * data[k][i]
# 分母
dummy_sum_dum += (U[k][j] ** m)
# 第i列的聚类中心
current_cluster_center.append(dummy_sum_num / dummy_sum_dum)
# 第j簇的所有聚类中心
C.append(current_cluster_center)
# 创建一个距离向量, 用于计算U矩阵。
distance_matrix = []
for i in range(0, len(data)):
current = []
for j in range(0, cluster_number):
current.append(distance(data[i], C[j]))
distance_matrix.append(current)
# 更新U
for j in range(0, cluster_number):
for i in range(0, len(data)):
dummy = 0.0
for k in range(0, cluster_number):
# 分母
dummy += (distance_matrix[i][j] / distance_matrix[i][k]) ** (2 / (m - 1))
U[i][j] = 1 / dummy
if end_conditon(U, U_old):
print("已完成聚类")
break
U = normalise_U(U)
return U
if __name__ == '__main__':
data = [[6.1, 2.8, 4.7, 1.2], [5.1, 3.4, 1.5, 0.2], [6.0, 3.4, 4.5, 1.6], [4.6, 3.1, 1.5, 0.2],
[6.7, 3.3, 5.7, 2.1], [7.2, 3.0, 5.8, 1.6], [6.7, 3.1, 4.4, 1.4], [6.4, 2.7, 5.3, 1.9],
[4.8, 3.0, 1.4, 0.3], [7.9, 3.8, 6.4, 2.0], [5.2, 3.5, 1.5, 0.2], [5.9, 3.0, 5.1, 1.8],
[5.7, 2.8, 4.1, 1.3], [6.8, 3.2, 5.9, 2.3], [5.4, 3.4, 1.5, 0.4], [5.4, 3.7, 1.5, 0.2],
[6.6, 3.0, 4.4, 1.4], [5.1, 3.5, 1.4, 0.2], [6.0, 2.2, 4.0, 1.0], [7.7, 2.8, 6.7, 2.0],
[6.3, 2.8, 5.1, 1.5], [7.4, 2.8, 6.1, 1.9], [5.5, 4.2, 1.4, 0.2], [5.7, 3.0, 4.2, 1.2],
[5.5, 2.6, 4.4, 1.2], [5.2, 3.4, 1.4, 0.2], [4.9, 3.1, 1.5, 0.1], [4.6, 3.6, 1.0, 0.2],
[4.6, 3.2, 1.4, 0.2], [5.8, 2.7, 3.9, 1.2], [5.0, 3.4, 1.5, 0.2], [6.1, 3.0, 4.6, 1.4],
[4.7, 3.2, 1.6, 0.2], [6.7, 3.3, 5.7, 2.5], [6.5, 3.0, 5.8, 2.2], [5.4, 3.4, 1.7, 0.2],
[5.8, 2.7, 5.1, 1.9], [5.4, 3.9, 1.3, 0.4], [5.3, 3.7, 1.5, 0.2], [6.1, 3.0, 4.9, 1.8],
[7.2, 3.2, 6.0, 1.8], [5.5, 2.3, 4.0, 1.3], [5.7, 2.8, 4.5, 1.3], [4.9, 2.4, 3.3, 1.0],
[5.4, 3.0, 4.5, 1.5], [5.0, 3.5, 1.6, 0.6], [5.2, 4.1, 1.5, 0.1], [5.8, 4.0, 1.2, 0.2],
[5.4, 3.9, 1.7, 0.4], [6.5, 3.2, 5.1, 2.0], [5.5, 2.4, 3.7, 1.0], [5.0, 3.5, 1.3, 0.3],
[6.3, 2.5, 5.0, 1.9], [6.9, 3.1, 4.9, 1.5], [6.2, 2.2, 4.5, 1.5], [6.3, 3.3, 4.7, 1.6],
[6.4, 3.2, 4.5, 1.5], [4.7, 3.2, 1.3, 0.2], [5.5, 2.4, 3.8, 1.1], [5.0, 2.0, 3.5, 1.0],
[4.4, 2.9, 1.4, 0.2], [4.8, 3.4, 1.9, 0.2], [6.3, 3.4, 5.6, 2.4], [5.5, 2.5, 4.0, 1.3],
[5.7, 2.5, 5.0, 2.0], [6.5, 3.0, 5.2, 2.0], [6.7, 3.0, 5.0, 1.7], [5.2, 2.7, 3.9, 1.4],
[6.9, 3.1, 5.1, 2.3], [7.2, 3.6, 6.1, 2.5], [4.8, 3.0, 1.4, 0.1], [6.3, 2.9, 5.6, 1.8],
[5.1, 3.5, 1.4, 0.3], [6.9, 3.1, 5.4, 2.1], [5.6, 3.0, 4.1, 1.3], [7.7, 2.6, 6.9, 2.3],
[6.4, 2.9, 4.3, 1.3], [5.8, 2.7, 4.1, 1.0], [6.1, 2.9, 4.7, 1.4], [5.7, 2.9, 4.2, 1.3],
[6.2, 2.8, 4.8, 1.8], [4.8, 3.4, 1.6, 0.2], [5.6, 2.9, 3.6, 1.3], [6.7, 2.5, 5.8, 1.8],
[5.0, 3.4, 1.6, 0.4], [6.3, 3.3, 6.0, 2.5], [5.1, 3.8, 1.9, 0.4], [6.6, 2.9, 4.6, 1.3],
[5.1, 3.3, 1.7, 0.5], [6.3, 2.5, 4.9, 1.5], [6.4, 3.1, 5.5, 1.8], [6.2, 3.4, 5.4, 2.3],
[6.7, 3.1, 5.6, 2.4], [4.6, 3.4, 1.4, 0.3], [5.5, 3.5, 1.3, 0.2], [5.6, 2.7, 4.2, 1.3],
[5.6, 2.8, 4.9, 2.0], [6.2, 2.9, 4.3, 1.3], [7.0, 3.2, 4.7, 1.4], [5.0, 3.2, 1.2, 0.2],
[4.3, 3.0, 1.1, 0.1], [7.7, 3.8, 6.7, 2.2], [5.6, 3.0, 4.5, 1.5], [5.8, 2.7, 5.1, 1.9],
[5.8, 2.8, 5.1, 2.4], [4.9, 3.1, 1.5, 0.1], [5.7, 3.8, 1.7, 0.3], [7.1, 3.0, 5.9, 2.1],
[5.1, 3.7, 1.5, 0.4], [6.3, 2.7, 4.9, 1.8], [6.7, 3.0, 5.2, 2.3], [5.1, 2.5, 3.0, 1.1],
[7.6, 3.0, 6.6, 2.1], [4.5, 2.3, 1.3, 0.3], [4.9, 3.0, 1.4, 0.2], [6.5, 2.8, 4.6, 1.5],
[5.7, 4.4, 1.5, 0.4], [6.8, 3.0, 5.5, 2.1], [4.9, 2.5, 4.5, 1.7], [5.1, 3.8, 1.5, 0.3],
[6.5, 3.0, 5.5, 1.8], [5.7, 2.6, 3.5, 1.0], [5.1, 3.8, 1.6, 0.2], [5.9, 3.0, 4.2, 1.5],
[6.4, 3.2, 5.3, 2.3], [4.4, 3.0, 1.3, 0.2], [6.1, 2.8, 4.0, 1.3], [6.3, 2.3, 4.4, 1.3],
[5.0, 2.3, 3.3, 1.0], [5.0, 3.6, 1.4, 0.2], [5.9, 3.2, 4.8, 1.8], [6.4, 2.8, 5.6, 2.2],
[6.1, 2.6, 5.6, 1.4], [5.6, 2.5, 3.9, 1.1], [6.0, 2.7, 5.1, 1.6], [6.0, 3.0, 4.8, 1.8],
[6.4, 2.8, 5.6, 2.1], [6.0, 2.9, 4.5, 1.5], [5.8, 2.6, 4.0, 1.2], [7.7, 3.0, 6.1, 2.3],
[5.0, 3.3, 1.4, 0.2], [6.9, 3.2, 5.7, 2.3], [6.8, 2.8, 4.8, 1.4], [4.8, 3.1, 1.6, 0.2],
[6.7, 3.1, 4.7, 1.5], [4.9, 3.1, 1.5, 0.1], [7.3, 2.9, 6.3, 1.8], [4.4, 3.2, 1.3, 0.2],
[6.0, 2.2, 5.0, 1.5], [5.0, 3.0, 1.6, 0.2]]
start = time.time()
# 调用模糊C均值函数
res_U = fuzzy(data, 3, 2)
# 计算准确率
print("用时:{0}".format(time.time() - start))