模糊C聚类(Fuzzy C-means Clustering, FCM)
文章目录
- 模糊C聚类(Fuzzy C-means Clustering, FCM)
-
- 1. 思想
- 2. 说明
- 3. 推导
-
- 3.1 初始条件
- 3.2 目标函数
- 3.3 最优化求解
- 3.4 问题解决
- 4. 实现
-
- 4.1 代码
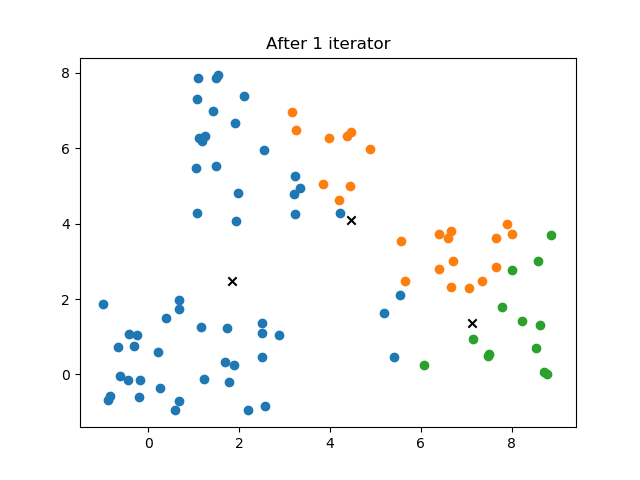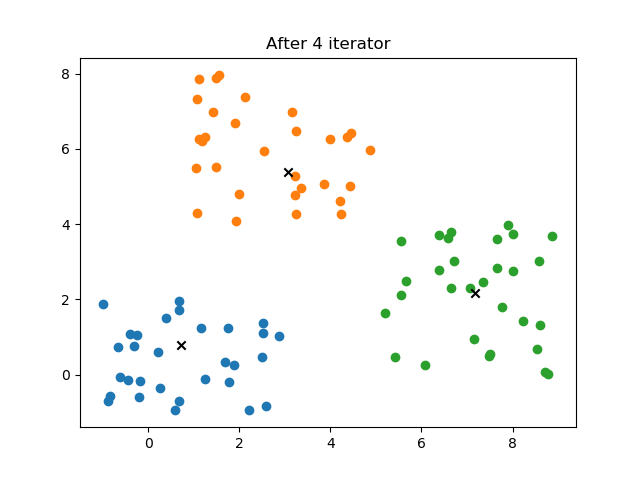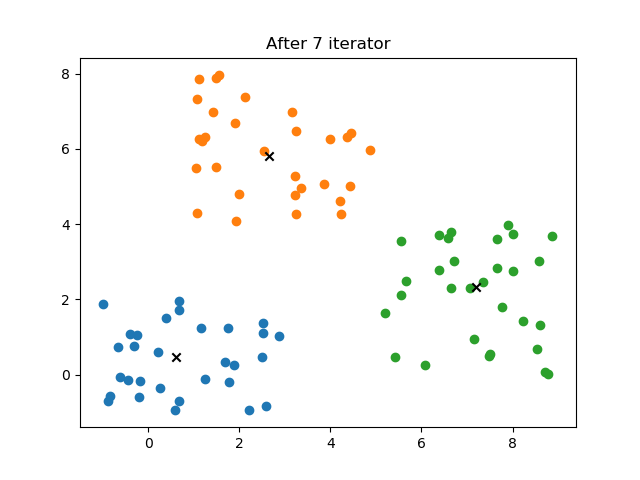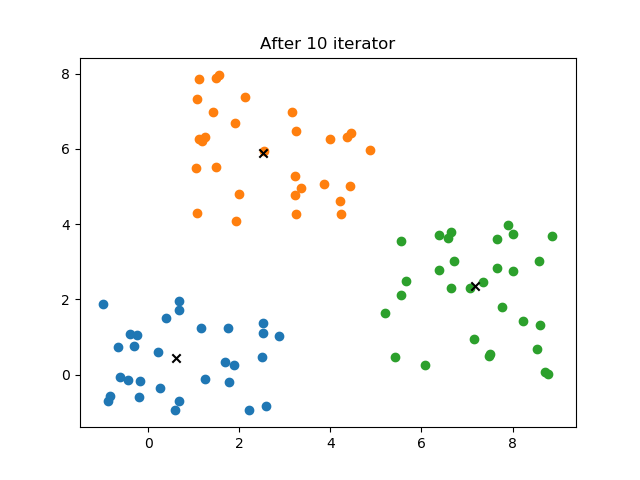
- 4.2 结果
模糊C聚类(Fuzzy C-means Clustering, FCM)
1. 思想
- 簇内距离尽量小(*)
- 簇间距离尽量大
2. 说明
-
某种程度上类似于 LDA 的思想,但他们间有明显差距,LDA是属于监督学习下的降维操作,而该聚类基于非监督;
-
过程跟k-means聚类类似,区别在于FCM计算了(中心)点到所有数据点的距离,增加了隶属于某一簇的概率值(隶属值),还有属于某一簇的重视程度 m ( > 1 \gt 1 >1)
3. 推导
3.1 初始条件
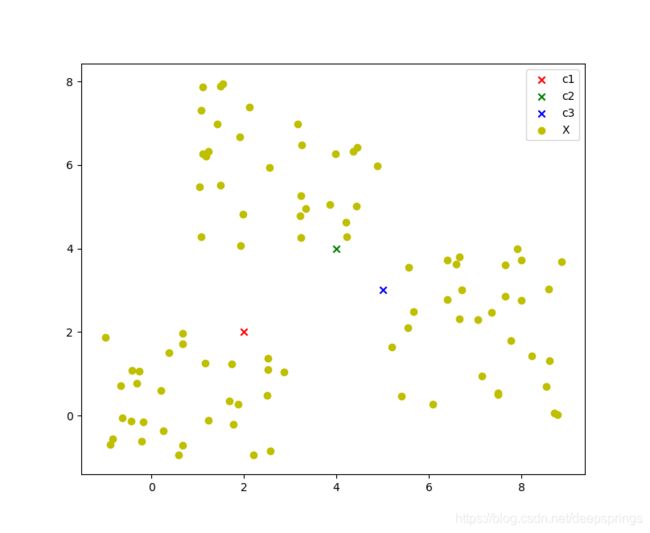
假设有N个原始数据点 X = ( x 1 , x 2 , ⋯ , x N ) X = (x_1, x_2, \cdots, x_N) X=(x1,x2,⋯,xN) ,设定有 L 个簇,初始簇心手动设定为 C = ( c 1 , c 2 , ⋯ , c l ) C=(c_1, c_2, \cdots, c_l) C=(c1,c2,⋯,cl) .
示意图如下(L=3时)
3.2 目标函数
计算每个数据点到簇心的距离(以到第一个簇心 c 1 c_1 c1为例)
d 1 = ∣ ∣ x 1 − c 1 ∣ ∣ 2 + ∣ ∣ x 2 − c 1 ∣ ∣ 2 + ⋯ + ∣ ∣ x N − c 1 ∣ ∣ 2 d_1 = ||x_1-c_1||^2+||x_2-c_1||^2+\cdots+||x_N-c_1||^2 d1=∣∣x1−c1∣∣2+∣∣x2−c1∣∣2+⋯+∣∣xN−c1∣∣2
为了表征一点到不同簇心的隶属程度,设定这些点到某一簇心的概率(隶属值,Membership values)为 u k i u_{ki} uki,该值表示第 i 点到第 k 个簇心的隶属值。点与簇心距离越大,该值越小。对于同一点来说,有
u 1 i + u 2 i + ⋯ + u L i = 1 u_{1i} + u_{2i} + \cdots + u_{Li} = 1 u1i+u2i+⋯+uLi=1
即,同一点到所有簇心隶属值和为 1
同时为了表示该点实实在在属于某一类,如图中右侧数据的某点属于 蓝色x 的重要程度更高,引入另一个参数:模糊系数(Fuzzifier) m
关于引入了隶属值 u k i u_{ki} uki 后为什么还要引入模糊系数m?
那么加权后,每个数据点到簇心 c 1 c_1 c1 的距离和为
d 1 ′ = u 11 m ∣ ∣ x 1 − c 1 ∣ ∣ 2 + u 12 m ∣ ∣ x 2 − c 1 ∣ ∣ 2 + ⋯ + u 1 N m ∣ ∣ x N − c 1 ∣ ∣ 2 = ∑ i = 1 N u 1 i m ∣ ∣ x i − c 1 ∣ ∣ 2 \begin{aligned} d'_1 &= u_{11}^m||x_1-c_1||^2 + u_{12}^m||x_2-c_1||^2 + \cdots + u_{1N}^m||x_N-c_1||^2 \\ &= \sum\limits_{i=1}^N u_{1i}^m||x_i-c_1||^2 \end{aligned} d1′=u11m∣∣x1−c1∣∣2+u12m∣∣x2−c1∣∣2+⋯+u1Nm∣∣xN−c1∣∣2=i=1∑Nu1im∣∣xi−c1∣∣2
对于所有点到所有簇心距离和为
D = ∑ k = 1 L ∑ i = 1 N u k i m ∣ ∣ x i − c k ∣ ∣ 2 D = \sum\limits_{k=1}^L \sum\limits_{i=1}^N u_{ki}^m||x_i-c_k||^2 D=k=1∑Li=1∑Nukim∣∣xi−ck∣∣2
该方程就是目标函数,优化方法是最小化该函数
M i n J ( u k i , c k ) = ∑ k = 1 L ∑ i = 1 N u k i m ∣ ∣ x i − c k ∣ ∣ 2 s . t ∑ k = 1 L u k i = 1 , i = 1 , 2 , ⋯ , N (1*) \begin{aligned}Min\ \ \ J(u_{ki}, c_k) &= \sum\limits_{k=1}^L \sum\limits_{i=1}^N u_{ki}^m||x_i-c_k||^2 \\s.t\ \ \sum\limits_{k=1}^L u_{ki} &= 1,\ \ i = 1,2,\cdots,N\end{aligned}\tag{1*} Min J(uki,ck)s.t k=1∑Luki=k=1∑Li=1∑Nukim∣∣xi−ck∣∣2=1, i=1,2,⋯,N(1*)
若 c k c_k ck 给定时, ∣ ∣ x i − c k ∣ ∣ 2 ||x_i-c_k||^2 ∣∣xi−ck∣∣2 为定值(假设为 d k i d_{ki} dki),因此也即是最小化
M i n J ( u k i ) = ∑ k = 1 L ∑ i = 1 N u k i m > d k i Min\ \ J(u_{ki}) = \sum\limits_{k=1}^L\sum\limits_{i=1}^N u_{ki}^m > d_{ki} Min J(uki)=k=1∑Li=1∑Nukim>dki
此时只与 u k i u_{ki} uki 相关。若隶属值 u k i u_{ki} uki 已知,同样可以得到
M i n J ( c k ) = ∑ k = 1 L ∑ i = 1 N u k i m ∣ ∣ x i − c k ∣ ∣ 2 Min\ \ J(c_k) = \sum\limits_{k=1}^L \sum\limits_{i=1}^N u_{ki}^m||x_i-c_k||^2 Min J(ck)=k=1∑Li=1∑Nukim∣∣xi−ck∣∣2
此时只与 c k c_k ck 相关。
3.3 最优化求解
推导过程
对于方程(1*)构造拉格朗日函数
L ( u k i , c k ) = ∑ k = 1 L ∑ i = 1 N u k i m ∣ ∣ x i − c k ∣ ∣ 2 − ∑ i = 1 N λ i ( ∑ k = 1 L u k i − 1 ) L(u_{ki},c_k) = \sum\limits_{k=1}^L \sum\limits_{i=1}^N u_{ki}^m||x_i-c_k||^2 - \sum\limits_{i=1}^N \lambda_i(\sum\limits_{k=1}^L u_{ki}-1) L(uki,ck)=k=1∑Li=1∑Nukim∣∣xi−ck∣∣2−i=1∑Nλi(k=1∑Luki−1)
极小值求解 (展开求导)
- 对 u k i u_{ki} uki
∂ L ∂ u k i = 0 ⇒ m u k i m − 1 ∣ ∣ x i − c k ∣ ∣ 2 − λ i = 0 ⇒ u k i = ( λ i m ∣ ∣ x i − c k ∣ ∣ 2 ) 1 m − 1 (*1) \begin{aligned}&\frac{\partial L}{\partial u_{ki}} = 0 \\\Rightarrow \ \ &mu_{ki}^{m-1}||x_i - c_k||^2 - \lambda_i = 0 \\\Rightarrow \ \ &u_{ki} = (\frac{\lambda_i}{m||x_i-c_k||^2})^{\frac{1}{m-1}} \\\end{aligned}\tag{*1} ⇒ ⇒ ∂uki∂L=0mukim−1∣∣xi−ck∣∣2−λi=0uki=(m∣∣xi−ck∣∣2λi)m−11(*1)
- 对 λ i \lambda_i λi
∂ L ∂ λ i = 0 ⇒ ∑ k = 1 L u k i − 1 = 0 ⇒ ∑ k = 1 L u k i = 1 (*2) \begin{aligned}&\frac{\partial L}{\partial \lambda_i} = 0 \\\ \ \Rightarrow & \sum\limits_{k=1}^L u_{ki} -1=0 \\\ \ \Rightarrow & \sum\limits_{k=1}^L u_{ki} = 1\end{aligned}\tag{*2} ⇒ ⇒∂λi∂L=0k=1∑Luki−1=0k=1∑Luki=1(*2)
联立(*1)和(*2),消去 λ i \lambda_i λi
∑ k = 1 L ( λ i m ∣ ∣ x i − c k ∣ ∣ 2 ) 1 m − 1 = 1 ( λ i m ) 1 m − 1 ∑ k = 1 L 1 ∣ ∣ x i − c k ∣ ∣ 2 m − 1 = 1 ( λ i m ) 1 m − 1 = 1 ∑ k = 1 L 1 ∣ ∣ x i − c k ∣ ∣ 2 m − 1 带 入 到 ( ∗ 1 ) ⇒ u k i = 1 ∣ ∣ x i − c k ∣ ∣ 2 m − 1 ∑ k = 1 L 1 ∣ ∣ x i − c k ∣ ∣ 2 m − 1 = 1 ∑ l = 1 L ( ∣ ∣ x i − c k ∣ ∣ ∣ ∣ x i − c l ∣ ∣ ) 2 m − 1 (*3) \begin{aligned}&\sum\limits_{k=1}^L (\frac{\lambda_i}{m||x_i-c_k||^2})^{\frac{1}{m-1}} = 1 \\ \\&(\frac{\lambda_i}{m})^{\frac{1}{m-1}} \sum\limits_{k=1}^L \frac{1}{||x_i-c_k||^{\frac{2}{m-1}}} = 1\\ \\&(\frac{\lambda_i}{m})^{\frac{1}{m-1}} = \frac{1}{\sum\limits_{k=1}^L \frac{1}{||x_i-c_k||^{\frac{2}{m-1}}}} \\ \\带入到(*1)&\Rightarrow u_{ki} = \frac{\frac{1}{||x_i-c_k||^{\frac{2}{m-1}}}}{\sum\limits_{k=1}^L \frac{1}{||x_i-c_k||^{\frac{2}{m-1}}}} = \frac{1}{\sum\limits_{l=1}^L (\frac{||x_i-c_k||}{||x_i-c_l||})^{\frac{2}{m-1}}}\end{aligned}\tag{*3} 带入到(∗1)k=1∑L(m∣∣xi−ck∣∣2λi)m−11=1(mλi)m−11k=1∑L∣∣xi−ck∣∣m−121=1(mλi)m−11=k=1∑L∣∣xi−ck∣∣m−1211⇒uki=k=1∑L∣∣xi−ck∣∣m−121∣∣xi−ck∣∣m−121=l=1∑L(∣∣xi−cl∣∣∣∣xi−ck∣∣)m−121(*3)
- 对 c k c_k ck
∂ L ∂ c k = 0 ⇒ ∑ i = 1 N u k i m ( − 2 ) ( x i − c k ) = 0 ⇒ ∑ i = 1 N u k i m x i = ∑ i = 1 N u k i m c k ⇒ c k = ∑ i = 1 N u k i m x i ∑ i = 1 N u k i m (*4) \begin{aligned}&\frac{\partial L}{\partial c_k} = 0 \\\ \ \Rightarrow &\sum\limits_{i=1}^N u_{ki}^m (-2)(x_i-c_k) = 0 \\\ \ \Rightarrow &\sum\limits_{i=1}^N u_{ki}^m x_i = \sum\limits_{i=1}^N u_{ki}^m c_k \\\ \ \Rightarrow &c_k = \frac{\sum\limits_{i=1}^N u_{ki}^m x_i }{\sum\limits_{i=1}^N u_{ki}^m}\end{aligned}\tag{*4} ⇒ ⇒ ⇒∂ck∂L=0i=1∑Nukim(−2)(xi−ck)=0i=1∑Nukimxi=i=1∑Nukimckck=i=1∑Nukimi=1∑Nukimxi(*4)
分析理解
主要得到两个方程(*3)和(*4),为方便理解,先不考虑模糊值 m ,此时有
u k i = 1 ∣ ∣ x i − c k ∣ ∣ 2 ∑ k = 1 L 1 ∣ ∣ x i − c k ∣ ∣ 2 (2*) u_{ki} =\frac{\frac{1}{||x_i-c_k||^{2}}}{\sum\limits_{k=1}^L \frac{1}{||x_i-c_k||^{2}}}\\\tag{2*} uki=k=1∑L∣∣xi−ck∣∣21∣∣xi−ck∣∣21(2*)
c k = ∑ i = 1 N u k i x i ∑ i = 1 N u k i (3*) c_k = \frac{\sum\limits_{i=1}^N u_{ki} x_i }{\sum\limits_{i=1}^N u_{ki}}\tag{3*} ck=i=1∑Nukii=1∑Nukixi(3*)
对于(2*), u k i u_{ki} uki 表示第 i 点隶属于 k 簇的概率值,且点到 k 簇的距离越大,该值越小,反之,越大,呈现负相关关系。而点到簇的距离为 ∣ ∣ x i − c k ∣ ∣ 2 ||x_i - c_k||^2 ∣∣xi−ck∣∣2 ,为了表示上述的负相关关系,可以使用该值的倒数,即 1 ∣ ∣ x i − c k ∣ ∣ 2 \frac{1}{||x_i-c_k||^2} ∣∣xi−ck∣∣21 ,而为了保证点到所有簇隶属值 u 的和为 1 ,分母除以该点到所有簇的总和,也即
u k i = 1 ∣ ∣ x i − c k ∣ ∣ 2 ∑ k = 1 L 1 ∣ ∣ x i − c k ∣ ∣ 2 u_{ki} =\frac{\frac{1}{||x_i-c_k||^{2}}}{\sum\limits_{k=1}^L \frac{1}{||x_i-c_k||^{2}}} uki=k=1∑L∣∣xi−ck∣∣21∣∣xi−ck∣∣21
同理, c k c_k ck 表示簇中心,(3*)可类比于质心求解公式。
3.4 问题解决
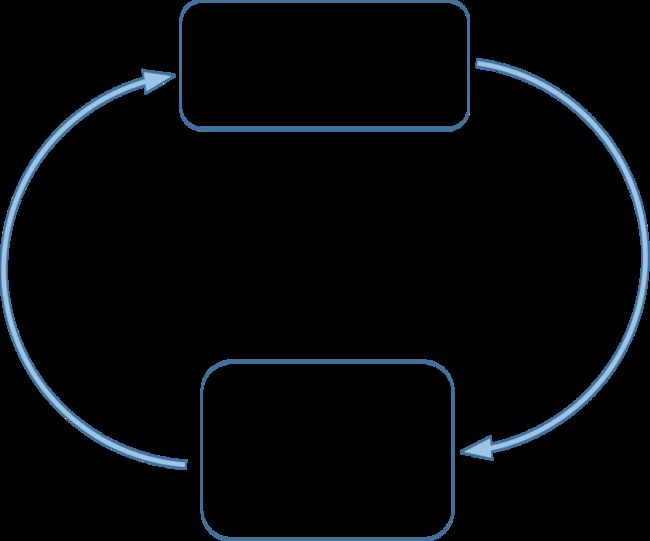
因此,对于上述问题,有两个步骤
- 在 c k c_k ck 给定情况下,可求解出 u k i u_{ki} uki
- 在 u k i u_{ki} uki 给定情况下,可求解出 c k c_k ck
这是一个循环过程,类比于 k-means 。用图示表示为
4. 实现
4.1 代码
import numpy as np
import matplotlib.pyplot as plt
import imageio
class FCM:
def __init__(self, data, m, c):
self.data = data # 原始数据
self.c = c # 起始簇
self.it = 0 # 迭代次数
self.m = m # 模糊值
self.N = len(self.data) # 原始数据个数
self.L = len(self.c) # 簇数
self.n = len(self.data[0]) # 数据维度
self.U = np.zeros((self.N, self.L)) # 隶属值
self.clusterIni(0)
def clusterIni(self, sig):
self.cluster = {} # 聚类
for i in range(self.L):
if i==0 and sig==0:
self.cluster[i] = data
else:
self.cluster[i] = []
def getU(self):
# 计算u矩阵
for _i,i in enumerate(self.data):
for _k,k in enumerate(self.c):
d = 0
for n in range(self.n):
d = d + (i[n]-k[n])**2
self.U[_i,_k] = np.power(1/d, 1/(self.m-1))
# 标记原始数据点隶属的簇类
cluster = []
for _u,u in enumerate(self.U):
s = np.sum(u)
for _l in range(self.L):
self.U[_u,_l] = self.U[_u,_l]/s
cluster.append(np.argmax(u))
# 记录簇数据
self.clusterIni(1)
for ind,dat in enumerate(self.data):
self.cluster[cluster[ind]].append(dat)
def getC(self):
# 重新计算簇心c
c = []
for l in range(self.L):
s1 = []
for n in range(self.n):
s1.append(0)
s2 = 0
for _i,i in enumerate(self.data):
u = self.U[_i,l]
for n in range(self.n):
s1[n] = s1[n] + np.power(u, self.m) * i[n]
s2 = s2 + np.power(u, self.m)
l = []
for n in range(self.n):
l.append(s1[n]/s2)
c.append(l)
# 判断是否已经收敛
if self.c == c:
return 0
else:
self.c = c
return 1
# 迭代
def iter(self, it):
for i in range(it):
self.getU()
b = self.getC()
self.it = self.it + 1
self.plot(1)
if not b:
print("总共迭代%d次"%(self.it-1))
break
def plot(self, isSave = 0):
# 显示簇
for c in self.cluster:
if(self.cluster[c] == []):
continue
x = np.array(self.cluster[c])[:,0]
y = np.array(self.cluster[c])[:,1]
plt.scatter(x, y)
# 显示中心点
mx = np.array(self.c)[:,0]
my = np.array(self.c)[:,1]
plt.scatter(mx, my, marker='x', color='black')
plt.title("After %d iterator"%self.it)
if isSave:
plt.savefig("./FCM/%d.png"%self.it)
plt.show()
if __name__ == '__main__':
# 原始数据
f = open('./clusterData.txt', 'r')
data = []
for _d in f:
dat = _d.rstrip().split(' ')
data.append([float(dat[0]), float(dat[1])])
f.close()
c = [[3,3],[6,5],[10,1]]
# FCM
obj = FCM(data, 3, c)
obj.iter(10)
# 可视化
inp = []
for i in range(obj.it):
inp.append(imageio.imread('./FCM/%d.png'%(i+1)))
outp = './FCM/fcm.gif'
imageio.mimsave(outp, inp, duration=1)