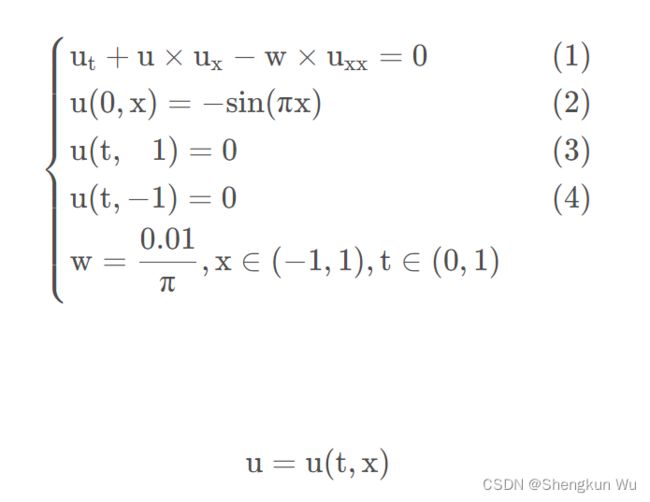神经网络求解PDE的一个范例

对于上述方程，求解的代码如下

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
import torch.optim as optim
import numpy as np



# 模型搭建
class Net(nn.Module):
    def __init__(self, NN): # NL n个l（线性，全连接）隐藏层， NN 输入数据的维数， 128 256
        super(Net, self).__init__()
        self.input_layer = nn.Linear(2, NN)
        self.hidden_layer1 = nn.Linear(NN,int(NN/2)) ## 原文这里用NN，我这里用的下采样，经过实验验证，“等采样”更优
        self.hidden_layer2 = nn.Linear(int(NN/2), int(NN/2))  ## 原文这里用NN，我这里用的下采样，经过实验验证，“等采样”更优
        self.output_layer = nn.Linear(int(NN/2), 1)

    def forward(self, x): # 一种特殊的方法 __call__() 回调
        out = torch.tanh(self.input_layer(x))
        out = torch.tanh(self.hidden_layer1(out))
        out = torch.tanh(self.hidden_layer2(out))
        out_final = self.output_layer(out)
        return out_final


def pde(x, net):
    u = net(x)  # 网络得到的数据
    u_tx = torch.autograd.grad(u, x, grad_outputs=torch.ones_like(net(x)),
                               create_graph=True, allow_unused=True)[0]  # 求偏导数
    d_t = u_tx[:, 0].unsqueeze(-1)
    d_x = u_tx[:, 1].unsqueeze(-1)
    
    u_xx = torch.autograd.grad(d_x, x, grad_outputs=torch.ones_like(d_x),
                               create_graph=True, allow_unused=True)[0][:,1].unsqueeze(-1)  # 求偏导数
    
    w = torch.tensor(0.01 / np.pi)
    return d_t + u * d_x - w * u_xx  # 公式（1）shape = [2000,1]


net = Net(30)
mse_cost_function = torch.nn.MSELoss(reduction='mean')  # Mean squared error
optimizer = torch.optim.Adam(net.parameters(), lr=1e-4)


# 初始化 常量
t_bc_zeros = np.zeros((2000, 1))
x_in_pos_one = np.ones((2000, 1))
x_in_neg_one = -np.ones((2000, 1))
u_in_zeros = np.zeros((2000, 1))

iterations = 1000
for epoch in range(iterations):
    optimizer.zero_grad()  # 梯度归0

    # 求边界条件的误差
    # 初始化变量
    t_in_var = np.random.uniform(low=0, high=1.0, size=(2000, 1))
    x_bc_var = np.random.uniform(low=-1.0, high=1.0, size=(2000, 1))
    u_bc_sin = -np.sin(np.pi * x_bc_var)

    # 将数据转化为torch可用的
    pt_x_bc_var = torch.from_numpy(x_bc_var).float().requires_grad_(False)
    pt_t_bc_zeros = torch.from_numpy(t_bc_zeros).float().requires_grad_(False)
    pt_u_bc_sin = torch.from_numpy(u_bc_sin).float().requires_grad_(False)
    pt_x_in_pos_one = torch.from_numpy(x_in_pos_one).float().requires_grad_(False)
    pt_x_in_neg_one = torch.from_numpy(x_in_neg_one).float().requires_grad_(False)
    pt_t_in_var = torch.from_numpy(t_in_var).float().requires_grad_(False)
    pt_u_in_zeros = torch.from_numpy(u_in_zeros).float().requires_grad_(False)
    
    # 求边界条件的损失
    net_bc_out = net(torch.cat([pt_t_bc_zeros, pt_x_bc_var], 1))  
    # t=0  and x in [-1,1], i.e. u(0,x)
    mse_u_2 = mse_cost_function(net_bc_out, pt_u_bc_sin)  
    # e = u(x,0)-(-sin(pi*x))  formula （2）
    

    net_bc_inr = net(torch.cat([pt_t_in_var, pt_x_in_pos_one], 1))  # 0=u(t,1) 公式（3)
    mse_u_3 = mse_cost_function(net_bc_inr, pt_u_in_zeros)  
    # e = 0-u(t,1) 公式(3)
    
    net_bc_inl = net(torch.cat([pt_t_in_var, pt_x_in_neg_one], 1))  # 0=u(t,-1) 公式（4）
    mse_u_4 = mse_cost_function(net_bc_inl, pt_u_in_zeros)  
    # e = 0-u(t,-1) formula （4）

    # 求PDE函数式的误差
    # 初始化变量
    x_collocation = np.random.uniform(low=-1.0, high=1.0, size=(2000, 1))
    t_collocation = np.random.uniform(low=0.0, high=1.0, size=(2000, 1))
    all_zeros = np.zeros((2000, 1))
    pt_x_collocation = torch.from_numpy(x_collocation).float().requires_grad_(True)
    pt_t_collocation = torch.from_numpy(t_collocation).float().requires_grad_(True)
    pt_all_zeros = torch.from_numpy(all_zeros).float().requires_grad_(False)
    f_out = pde(torch.cat([pt_t_collocation, pt_x_collocation], 1), net)  # output of f(x,t) 公式（1）
    mse_f_1 = mse_cost_function(f_out, pt_all_zeros)
    
    # 将误差(损失)累加起来
    loss = mse_f_1 + mse_u_2 + mse_u_3 + mse_u_4
    
    loss.backward()  # 反向传播
    optimizer.step()  # This is equivalent to : theta_new = theta_old - alpha * derivative of J w.r.t theta
    with torch.autograd.no_grad():
        if epoch % 100 == 0:
            print(epoch, "Traning Loss:", loss.data)