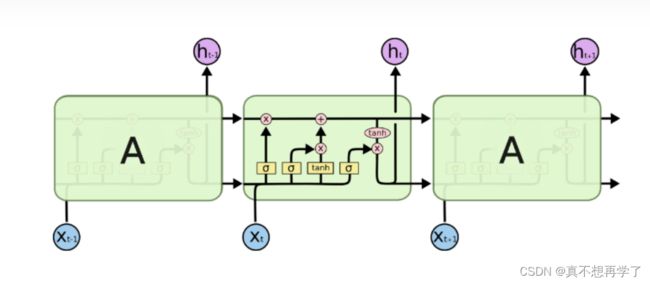
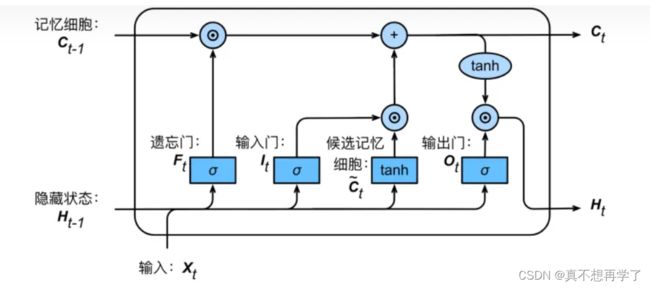
NNDL 作业10:第六章课后题(LSTM | GRU)
习题6-3 当使用公式(6.50)作为循环神经网络得状态更新公式时,分析其可能存在梯度爆炸的原因并给出解决办法.
公式(6.50):
h t = h t − 1 + g ( x t , h t − 1 ; Θ ) h_{t}=h_{t-1}+g(x_{t},h_{t-1};\Theta ) ht=ht−1+g(xt,ht−1;Θ)
令 Z k = U h k − 1 + W x k + b Z_k=Uh_{k-1}+Wx_k+b Zk=Uhk−1+Wxk+b为在第k时刻函数g(·)的输入,在计算公式
δ t , k = ∂ L t ∂ z k \delta _{t,k} = \frac{\partial L_t}{\partial z_k} δt,k=∂zk∂Lt
中的误差项 z k = U h k − 1 + W x k + b z_k=Uh_{k-1}+Wx_k+b zk=Uhk−1+Wxk+b时,梯度可能会过大,从而导致梯度爆炸问题.
解决方式:
1.更换激活函数,比如可以选择 ReLU 函数。
2.更改 RNN 隐藏层的结构,比如采用 GRU 或者 LSTM 的隐藏层结构。
习题6-4 推导LSTM网络中参数的梯度,并分析其避免梯度消失的效果
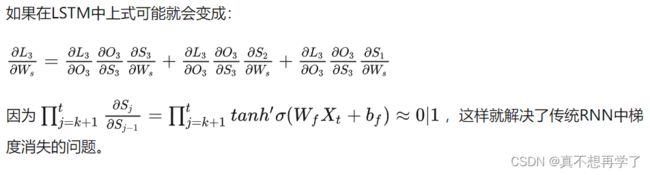
LSTM 中通过门的作用,可以使连乘项约等于 0 或者 1。因此当门的梯度接近1时,连乘项能够保证梯度很好地在 LSTM 中传递,避免梯度消失的情况发生。
而当门的梯度接近 0 时,意味着上一时刻的信息对当前时刻并没有作用,此时没有必要把梯度回传。
这就是 LSTM 能够克服梯度消失、梯度爆炸的原因。
ref:
https://zhuanlan.zhihu.com/p/156932219
习题6-5 推导GRU网络中参数的梯度,并分析其避免梯度消失的效果
GRU 是 LSTM 的一种变种,结构比 LSTM 简单一点。LSTM有三个门 (遗忘门 forget,输入门 input,输出门output),而 GRU 只有两个门 (更新门 update,重置门 reset)。另外,GRU 没有 LSTM 中的 cell 状态 c。

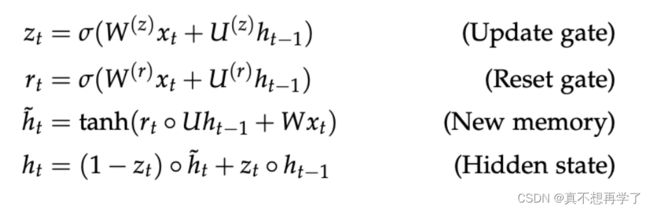
推导一下GRU参数的迭代过程:
针对于时刻t,使用链式求导法则,计算参数矩阵的梯度,其中E是代价函数,首先计算对隐层输出的梯度,因为隐层输出牵涉到多个时刻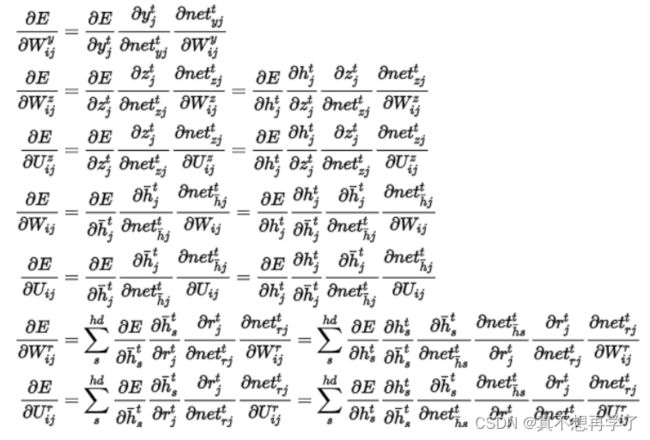
令:
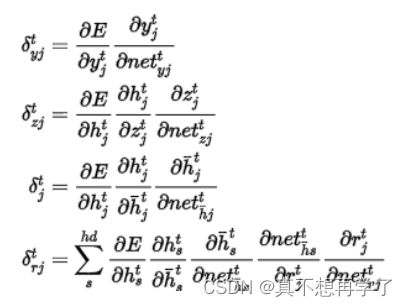
则:
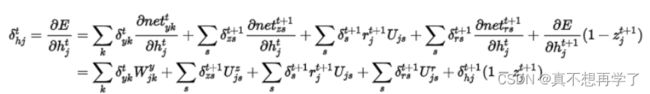
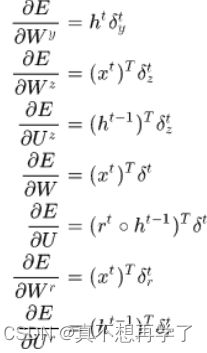
重置门 rt 控制着前一状态的信息 ht-1 传入候选状态 (图中带波浪线的ht) 的比例,重置门 rt 的值越小,则与 ht-1 的乘积越小,ht-1 的信息添加到候选状态越少。更新门用于控制前一状态的信息 ht-1 有多少保留到新状态 ht 中,当 (1-zt) 越大,保留的信息越多。
ref:
https://www.cnblogs.com/YiXiaoZhou/p/6075777.html
https://www.jianshu.com/p/247a72812aff
附加题 6-1P 什么时候应该用GRU? 什么时候用LSTM?
二者的对比:
GRU的优点是其模型的简单性 ,因此更适用于构建较大的网络。它只有两个门控,从计算角度看,它的效率更高,它的可扩展性有利于构筑较大的模型;而LSTM就更加的灵活,因为它具有三个门控。
但是究竟孰优孰劣,还是得具体情况具体分析。
附加题 6-2P LSTM BP推导,并用Numpy实现
上面推过了,简单实现:
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
def softmax(x):
e_x = np.exp(x-np.max(x))# 防溢出
return e_x/e_x.sum(axis=0)
def LSTM_CELL_Forward(xt, h_prev, C_prev, parameters):
Wf = parameters["Wf"]
bf = parameters["bf"]
Wi = parameters["Wi"]
bi = parameters["bi"]
Wc = parameters["Wc"]
bc = parameters["bc"]
Wo = parameters["Wo"]
bo = parameters["bo"]
Wy = parameters["Wy"]
by = parameters["by"]
# 获取 xt 和 Wy 的维度参数
n_x, m = xt.shape
n_y, n_h = Wy.shape
# 拼接 h_prev 和 xt
concat = np.zeros((n_x + n_h, m))
concat[: n_h, :] = h_prev
concat[n_h:, :] = xt
# 计算遗忘门、输入门、记忆细胞候选值、下一时间步的记忆细胞、输出门和下一时间步的隐状态值
ft = sigmoid(np.dot(Wf, concat) + bf)
it = sigmoid(np.dot(Wi, concat) + bi)
cct = np.tanh(np.dot(Wc, concat) + bc)
c_next = ft * c_prev + it * cct
ot = sigmoid(np.dot(Wo, concat) + bo)
h_next = ot * np.tanh(c_next)
# LSTM单元的计算预测
yt_pred = softmax(np.dot(Wy, h_next) + by)
return h_next, c_next, yt_pred
np.random.seed(1)
xt = np.random.randn(3,10)
h_prev = np.random.randn(5,10)
c_prev = np.random.randn(5,10)
Wf = np.random.randn(5, 5+3)
bf = np.random.randn(5,1)
Wi = np.random.randn(5, 5+3)
bi = np.random.randn(5,1)
Wo = np.random.randn(5, 5+3)
bo = np.random.randn(5,1)
Wc = np.random.randn(5, 5+3)
bc = np.random.randn(5,1)
Wy = np.random.randn(2,5)
by = np.random.randn(2,1)
parameters = {"Wf": Wf, "Wi": Wi, "Wo": Wo, "Wc": Wc, "Wy": Wy, "bf": bf, "bi": bi, "bo": bo, "bc": bc, "by": by}
h_next, c_next, yt = LSTM_CELL_Forward(xt, h_prev, c_prev, parameters)
print("a_next[4] = ", h_next[4])
print("a_next.shape = ", c_next.shape)
print("c_next[2] = ", c_next[2])
print("c_next.shape = ", c_next.shape)
print("yt[1] =", yt[1])
print("yt.shape = ", yt.shape)
a_next[4] = [-0.66408471 0.0036921 0.02088357 0.22834167 -0.85575339 0.00138482
0.76566531 0.34631421 -0.00215674 0.43827275]
a_next.shape = (5, 10)
c_next[2] = [ 0.63267805 1.00570849 0.35504474 0.20690913 -1.64566718 0.11832942
0.76449811 -0.0981561 -0.74348425 -0.26810932]
c_next.shape = (5, 10)
yt[1] = [0.79913913 0.15986619 0.22412122 0.15606108 0.97057211 0.31146381
0.00943007 0.12666353 0.39380172 0.07828381]
yt.shape = (2, 10)
Process finished with exit code 0
总结;
总体感觉难度还是很大的,主要是链式求导太麻烦了。LSTM和GRU都是为了缓解梯度爆炸而设计的,而GRU的结构更加简单,都是为了解决RNN的长程依赖问题。而且两个网络的主要思想都是增加了一条记忆总线(最上面那条),使得网络的记忆更加长久一些。通过几个门控单元对网络的细节进行调整。