《Beta Embeddings for Multi-Hop Logical Reasoning in Knowledge Graphs》论文阅读笔记
《Beta Embeddings for Multi-Hop Logical Reasoning in Knowledge Graphs》论文阅读笔记
主要挑战贡献:
KG上的推理挑战主要有两个:1.KG的规模很大,每跳一步候选答案集的候选答案数量便指数增长,因此通过跳转来寻找答案不现实;2.绝大多数的现实世界的KG根本不完全,缺少很多边(关系),因此跳转可能都跳不动,根本无法找到答案。
BetaE是第一个可以在大型异构知识图谱上处理**所有逻辑操作符号(包括存在、交、或、非,之前主要是无法处理逻辑“非”)的方法,它具有embedding类方法的隐含归纳关系**的能力、并且可以建模实体语义的不确定性,极大的增强了真实世界知识图谱上多跳推理的可拓展性和处理能力。
原文摘要:
人工智能的基本问题之一是对知识图(KG)捕获的事实执行复杂的多跳逻辑推理。这个问题具有挑战性,因为KG可能庞大且不完整。最近的方法将KG实体嵌入到低维空间中,然后使用这些嵌入来找到答案实体。但是,由于当前方法仅限于FOL(一阶逻辑)运算符的一个子集,因此如何处理任意的一阶逻辑(FOL)查询一直是一个严峻的挑战。特别是,不支持(¬)运算符。当前方法的另一个局限性在于它们不能自然地对不确定性建模。
在这里,我们介绍BETAE,这是一个概率嵌入框架,用于回答KG上的任意FOL查询。 BETAE是第一种可以处理一阶逻辑运算全集:合取(∧),析取(∨)和取反(¬)的方法。 BETAE的一个关键idea是使用有限支持下的概率分布,具体来说就是Beta分布,并将查询/实体作为Beta分布嵌入,因此,我们也可以对不确定性进行建模。逻辑操作是由神经运算符在概率嵌入中在嵌入空间中执行的。我们展示了BETAE在回答三个大型不完整KG上的任意FOL查询时的性能。与一般的KG推理方法相比,BETAE更为通用,它的相对性能也提高了25.4%,后者只能处理合取查询而没有取反操作。
相关工作:
1.KGE(trans、convE、transG/KG2E)以链接预测为目标,并不知道怎么泛化这些方法到使用逻辑操作的多跳知识图谱推理
2.建模不确定性,使用order embedding、分布、量子逻辑
I. Vendrov, R. Kiros, S. Fidler, and R. Urtasun, “Order-embeddings of images and language,” in International Conference on Learning Representations (ICLR), 2016.
S. He, K. Liu, G. Ji, and J. Zhao, “Learning to represent knowledge graphs with gaussian embedding,” in Proceedings of the 24th ACM International on Conference on Information and Knowledge Management, 2015.
D. Garg, S. Ikbal, S. K. Srivastava, H. Vishwakarma, H. Karanam, and L. V. Subramaniam, “Quantum embedding of knowledge for reasoning,” in Advances in Neural Information Processing Systems (NeurIPS), 2019.
3.知识图谱多跳推理-回答多跳逻辑查询(GQE、Q2B)
K. Guu, J. Miller, and P. Liang, “Traversing knowledge graphs in vector space,” in Empirical Methods in Natural Language Processing (EMNLP), 2015.
R. Das, A. Neelakantan, D. Belanger, and A. McCallum, “Chains of reasoning over entities, relations, and text using recurrent neural networks,” in European Chapter of the Association for Computational Linguistics (EACL), 2017.
4.知识图谱多跳推理-使用多跳规则或路径来提高链接预测准确度(Deeppath)
W. Xiong, T. Hoang, and W. Y. Wang, “Deeppath: A reinforcement learning method for knowledge graph reasoning,” in Empirical Methods in Natural Language Processing (EMNLP), 2017.
X. V. Lin, R. Socher, and C. Xiong, “Multi-hop knowledge graph reasoning with reward shaping,” in Empirical Methods in Natural Language Processing (EMNLP), 2018.
X. Chen, M. Chen, W. Shi, Y. Sun, and C. Zaniolo, “Embedding uncertain knowledge graphs,” in AAAI Conference on Artificial Intelligence (AAAI), 2019.
S. Guo, Q. Wang, L. Wang, B. Wang, and L. Guo, “Knowledge graph embedding with iterative guidance from soft rules,” in AAAI Conference on Artificial Intelligence (AAAI), 2018.
S. Guo, Q. Wang, L. Wang, B. Wang, and L. Guo, “Jointly embedding knowledge graphs and logical rules,” in Empirical Methods in Natural Language Processing (EMNLP), 2016.
H. Wang, H. Ren, and J. Leskovec, “Entity context and relational paths for knowledge graph completion,” arXiv preprint arXiv:2002.06757, 2020.
基础概念:
-推理:从已知知识/事实中获得逻辑结论或者作出预测的过程
-知识图谱推理:本质上是使用存在(∃)、与(∧)、或(∨)、非(¬)四种逻辑操作来回答KG上的一阶逻辑查询
-一阶逻辑查询:一阶逻辑是一种将自然语言形式化为可计算格式的方法,由非变量锚实体集,存在性量化变量集、单目标变量组成,详见维基百科,下面的例子中分别对应*(Europe、worldcup)、(V)、(V?)*。
-推理过程:给定一个一阶逻辑查询q,将其解析为一个计算图computation graph,这个计算图明确了来找到答案所需要的所有步骤,按照步骤可以推理出最终答案。
-举例:欧洲没有举办过世界杯的国家的总统有哪些?
步骤1.写成FOL形式:= ? . ∃ ∶ ( ,) ∧ ¬ ( , )∧ ( , ?)
步骤2.画出对应计算图
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MM1RHDin-1617950564050)(https://i.loli.net/2021/02/06/QhfBF57kqjEUWuK.png)]
步骤3.按照计算图执行定义好的逻辑操作,绿色节点就是我们的目标答案
显而易见,推理方法的关键就在于如何嵌入实体和查询、如何定义逻辑操作,这也就是所有模型的主要创新点。
补充:处理disjunction 或操作(∨)时可以将其转化为DNF-disjunctive normal form和DM-De Morgan’s laws两种方式,本文采用的是DM(根据德摩根定律:多个集合的并集等价于各个集合补集的交集的补集,因此就可以用交和非来表示或操作),但是后续的实验证明DNF更好,因为它能表示disjunction用多最大值的embedding。但是,证明了DM能够提供或操作很好的近似,并且泛化性不错。重要的是,betaE很灵活,可以DNF也可以DM,baseline只能DNF
具体模型:
解决关键问题:主要包括如何定义实体和查询的嵌入形式、如何定义在该嵌入形式上实现对应的逻辑操作
1-嵌入方式:
GQE把查询和实体都嵌入到欧几里得空间中的点向量;Q2B把查询嵌入成超几何盒子、把实体嵌入成可以被包含在里面的点向量;二者都设计了他们的projection和intersection操作,但是二者都不能处理非操作,因为无论是欧几里得空间的点或者盒子,他们的补集都不在欧几里得空间中。
为了解决这个问题,希望的embedding属性包括:能够自然建模不确定性并且可以设计封闭的逻辑操作。为什么要封闭?1.能够实现非操作,并且操作可以随意结合,2.使在增加逻辑操作时,embedding表示保持在固定的空间/时间复杂度,不会指数增长
因此,BetaE采用了Beta分布来作为实体entity和查询query的嵌入(在这里补充一个观点,embedding嵌入是啥都可以,不一定是向量,只是最终呈现出可用于计算的向量形式),那么beta分布是啥呢?
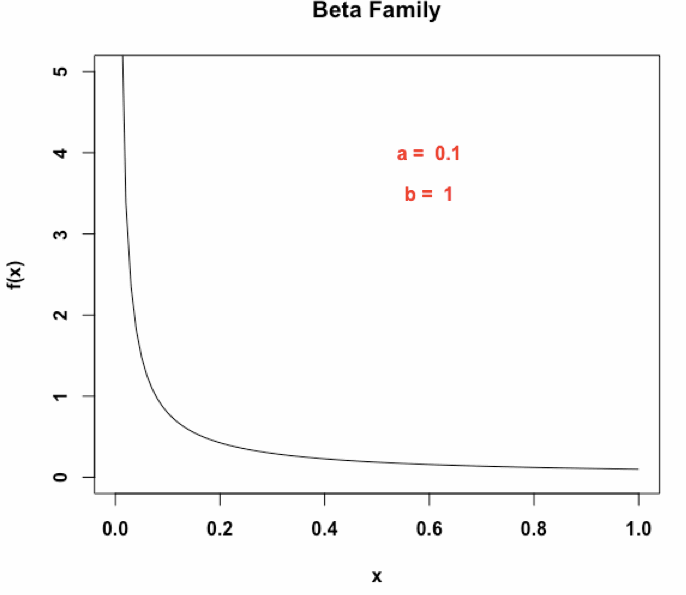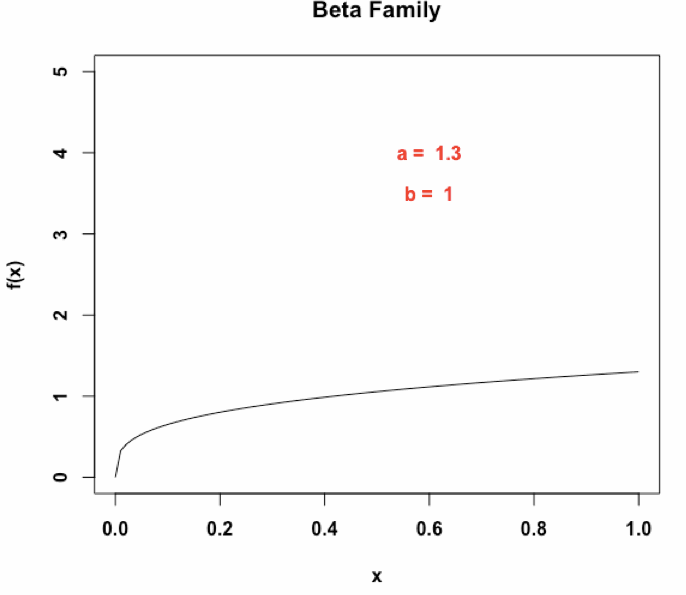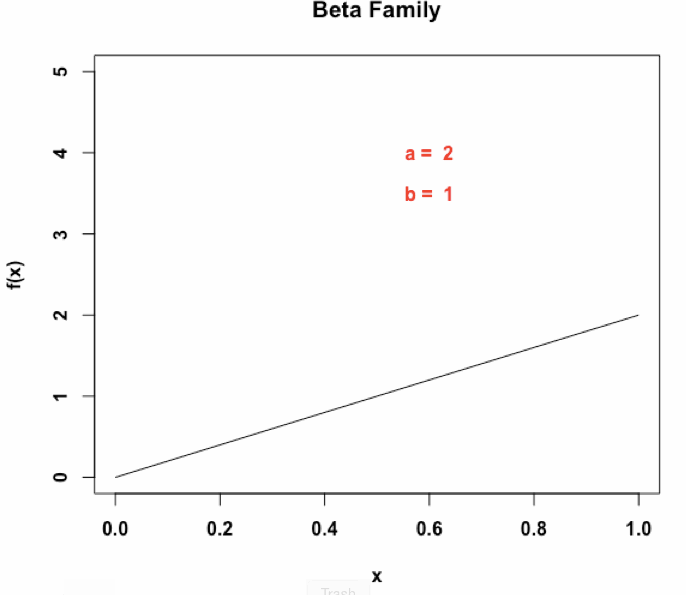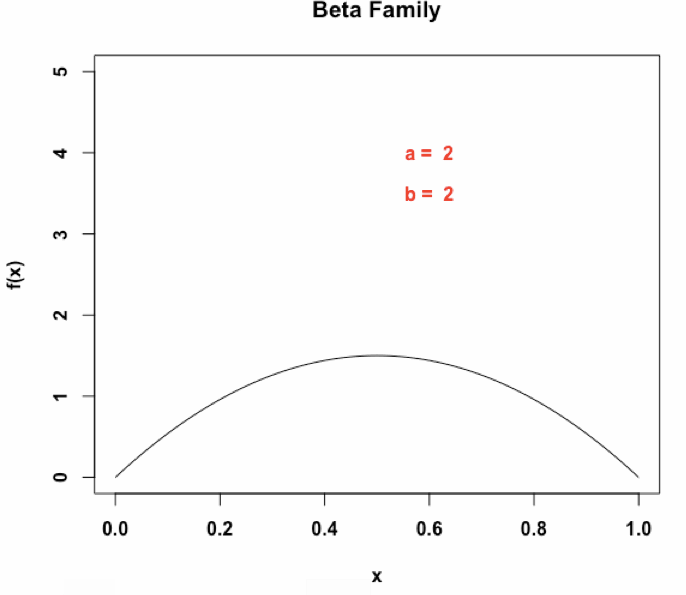
具体来说,一个Beta(α, β )分布有两个形状参数α, β,决定了上面他的概率密度函数(原文缩写为PDF)的形状,有高概率密度和低概率密度等不同的区域。并且一个Beta(α, β )分布的不确定性可以通过微分熵进行计算。那么,对于一个实体entity,我们赋予它一个beta embedding:
S = [(α1, β1), . . . , (αn, βn)],
每一个Beta embedding由n(超参数)个独立的Beta分布组成,2n维度,用于获取给定实体或者查询的不同方面的特征,为了便于说明,下面的n=1进行解释
2-逻辑操作:
由于DM定律的存在,我们只用定义三种逻辑操作符号:Relation Projection(关系投影)、Intersection(交)、Negation(非)
- Probabilistic Projection Operator P:输入一个beta embedding S,输出一个beta embedding S ′,本质上是为每个关系学习一个MLP,把2n维向量
S ′ = M L P r ( S ) S ′ = MLP r (S) S′=MLPr(S)
- Probabilistic Intersection Operator I:输入一个beta embedding集合
S 1 , . . . , S n { {S 1, . . . , S n}} S1,...,Sn
输出一个beta emdedding Ps_inter,本质上是把交操作建模为多个Beta嵌入的概率密度分布的加权积,其中的权重wi通过注意力机制获得:
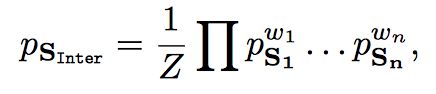

其实在具体计算参数操作上,等价于把n维beta向量,按维度相加:
S i n t e r = [ ( ∑ w i α i , ∑ w i β i ) ] Sinter=[( ∑ w iα i, ∑ w iβ i)] Sinter=[(∑wiαi,∑wiβi)]
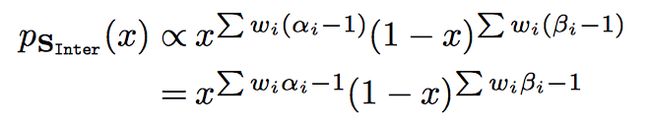
-
Probabilistic Negation Operator N:输入一个Beta embedding S,输出一个补集Beta embedding N(S),本质上在参数向量的计算上就是把两个参数取倒数:
N ( [ ( α , β ) ] ) = [ ( 1 / α , 1 / β ) ] N([(α, β )]) = [( 1/α , 1/β )] N([(α,β)])=[(1/α,1/β)]让我们回头看一下这三个操作的性质:关系投影P用MLPr学习关系属于常规操作,不需要赘述;交操作I等价于beta参数加权和;非操作等价于beta参数取倒数,并且加权和和取倒数对于beta分布的影响成功符合了我们直觉上对交和非的理解,在交操作加权和下,众多beta分布的交分布的高概率密度区域取到了绝大多数分布的高概率密度区域,低者亦然;在非操作下,高低概率密度区域互换。
3-学习过程:
对于一个查询query,通过计算图上的计算,最终将它嵌入成一个beta embedding q,通过计算q与候选答案v的距离,进行排序得到最终的推理结果。距离定义为KL散度:
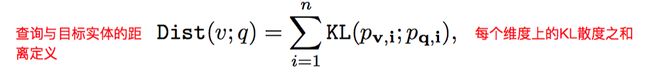
使用基于负采样的最大间隔化的损失函数进行训练: