机器学习实验 - K均值聚类

报告内容仅供学习参考，请独立完成作业和实验喔~

一、报告摘要

1.1 实验要求

（1）了解无监督任务范式概念，掌握聚类思想。
（2）掌握K-means算法，编程实现K-means。
（3）基于鸢尾花数据集，使用聚类纯度、兰德系数和F1值评测聚类效果。

1.2 实验思路

\qquad 使用Python读取鸢尾花三分类数据集并训练最佳的K-Means模型，随后使用生成的模型将数据进行聚类，并根据使用聚类纯度、兰德系数和F1值评测聚类效果。

1.3 实验结论

\qquad 本实验训练了一个K-Means模型，并对鸢尾花三分类数据集进行聚类，测试得到聚类纯度为0.96，兰德系数为0.9495，F1值为0.9233，模型表现效果较好。

二、实验内容

2.1 方法介绍

（1）监督学习与无监督学习
\qquad 监督学习是根据已有数据集，知道输入和输出结果之间的关系，然后根据这种已知关系训练得到一个最优模型。也就是说，在监督学习中，我们的训练数据应该既有特征又有标签，然后通过训练，使得机器能自己找到特征和标签之间的联系，然后在面对没有标签的数据时可以判断出标签。在监督学习的范畴中，又可以划分为回归和分类，常见算法有KNN、决策树、朴素贝叶斯等。
\qquad 无监督学习和监督学习最大的不同是监督学习中数据是带有一系列标签。在无监督学习中，我们需要用某种算法去训练无标签的训练集从而能让我们找到这组数据的潜在结构。无监督学习大致可以分为聚类和降维两大类，其中聚类是无监督学习中研究最多、应用最广的算法，常见算法有K-Means、BIRCH、GMM等。
（2）聚类思想
\qquad 聚类（Clustering）是一种典型的“无监督学习”，是把物理对象或抽象对象的集合分组为由彼此类似的对象组成的多个类的分析过程。
\qquad 聚类试图将数据集中的样本划分为若干个通常是不相交的子集，每个子集对应一个簇。与分类的不同在于，聚类所要求的划分的类别是未知，类别个数也是未知的。聚类的目标为簇内相似度尽可能高，簇间相似度尽可能低。
\qquad 常见算法有K-Means、DBSCAN、BIRCH、OPTICS、Agglomerative等。
（3）K均值聚类算法K-Means
\qquad K-means是一种常用的基于欧式距离的聚类算法，其认为两个目标的距离越近，相似度越大。其算法流程如下：

K-Means方法有以下优点：

• 原理简单、实现容易；
• 聚类效果相对较优；
• 可调参数仅为k。

也有以下缺点：

• 非凸数据集难以收敛；
• k值选择难以确定；
• 对于非平衡数据，聚类效果不佳；
• 对噪声和异常点比较敏感。

2.2 实验细节

2.2.1 实验环境

硬件环境：Intel® Core™ i5-10300H CPU + 16G RAM
软件环境：Windows 11 家庭中文版 + Python 3.8

2.2.2 实验过程

（1）训练K-Means模型
\qquad 根据数据，我们已知鸢尾花分3类，因此我们这里的聚类数k=3。利用sklearn的KMeans()方法训练K-Means模型，并将结果用散点图表示，实现代码及结果如下：

#训练KMeans模型
estimator = KMeans(n_clusters=3)
estimator.fit(X)#聚类

#绘制结果散点图
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:, 0], x0[:, 1], c = "red", marker='o', label='label0')  
plt.scatter(x1[:, 0], x1[:, 1], c = "green", marker='*', label='label1')  
plt.scatter(x2[:, 0], x2[:, 1], c = "blue", marker='+', label='label2')  
plt.xlabel('petal length')  
plt.ylabel('petal width')  
plt.legend(loc=2)  
plt.show()  

(2)计算聚类纯度、兰德系数和F1值，评测聚类效果
\qquad 使用sklearn.metrics库中提供的pair_confusion_matrix()方法求得当前聚类的混淆矩阵，随后利用聚类纯度、兰德系数和F1值的计算公式计算得到当前聚类效果的相应指标值。聚类纯度、兰德系数和F1值的具体计算公式见2.4评价指标介绍部分。
\qquad 以下为该部分代码及计算结果：

#聚类纯度
def accuracy(labels_true, labels_pred):
    clusters = np.unique(labels_pred)
    labels_true = np.reshape(labels_true, (-1, 1))
    labels_pred = np.reshape(labels_pred, (-1, 1))
    count = []
    for c in clusters:
        idx = np.where(labels_pred == c)[0]
        labels_tmp = labels_true[idx, :].reshape(-1)
        count.append(np.bincount(labels_tmp).max())
    return np.sum(count) / labels_true.shape[0]
#兰德系数、F1值
def get_rand_index_and_f_measure(labels_true, labels_pred, beta=1.):
    (tn, fp), (fn, tp) = pair_confusion_matrix(labels_true, labels_pred)
    ri = (tp + tn) / (tp + tn + fp + fn)
    p, r = tp / (tp + fp), tp / (tp + fn)
    f_beta = 2*p*r/(p+r)
    return ri, f_beta
#输出结果
purity = accuracy(y, y_pred)
ri, f_beta = get_rand_index_and_f_measure(y, y_pred, beta=1.)
print(f"聚类纯度：{purity}\n兰德系数：{ri}\nF1值：{f_beta}")

（3）调整数据，提升聚类效果
\qquad 根据上述介绍，可知在不修改模型的前提下，想提升聚类效果可以从数据维度和分类数两点下手改进。由于我们这里已经确定是三分类，因此可修改的只有数据维度这一点。
\qquad 在之前的实验中，采用的特征为数据集给出的全部特征，得到的结果虽然分出三类，但绿色label1和蓝色label2这两类的界限并不清晰。因此考虑减少数据维度再测试。
\qquad 当选取3个数据维度时，部分可能的效果如下图所示：
\qquad 1）选取维度1、2、3时，聚类纯度0.88

\qquad 2）选取维度2、3、4时，聚类纯度0.9533

\qquad 当选取两个维度时，考虑到数据的实际意义，即前两个维度代表萼片长宽、后两个维度代表花瓣长宽，分别选取前两个维度和后两个维度进行聚类测试，效果如下：
\qquad 1）选取前两个维度，聚类纯度0.82

\qquad 2）选取后两个维度，聚类纯度0.96

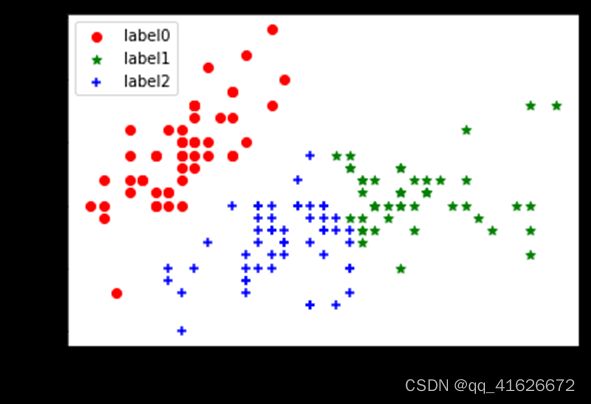
\qquad 经过比较，可以得出以下结论，当仅选取后两个数据维度时，对鸢尾花数据集进行三分类，可以得到最好的结果。

2.2.3 实验与理论内容的不同点

\qquad 实验与理论内容的主要区别在于聚类数量k和数据的处理上。
\qquad 在具体实验时，要通过大量的实验测试、对数据意义的分析以及任务需求，推断得到最合适的聚类数量K进行聚类。此外，在数据处理上，并不是一定是数据维度越多越好，数据处理要能为完成任务目标服务，使获得最好的聚类效果。

2.3 实验数据介绍

\qquad 实验数据为来自UCI的鸢尾花三分类数据集Iris Plants Database。
\qquad 数据集共包含150组数据，分为3类，每类50组数据。每组数据包括4个参数和1个分类标签，4个参数分别为：萼片长度sepal length、萼片宽度sepal width、花瓣长度petal length、花瓣宽度petal width，单位均为厘米。分类标签共有三种，分别为Iris Setosa、Iris Versicolour和Iris Virginica。
\qquad 数据集格式如下图所示：

\qquad 为方便使用，也可以直接使用sklearn.datasets库中的load_iris()方法直接加载该数据集。

2.4 评价指标介绍

\qquad 由于本次为聚类任务，因此使用聚类相关的混淆矩阵和评价指标。
\qquad 聚类任务中的混淆矩阵与普通混淆矩阵的意义有一定区别，如下表所示：

	同簇	非同簇
同类	TP	FN
非同类	FP	TN

\qquad 其中，TP为两个同类样本在同一簇的数量；FP为两个非同类样本在同一簇的数量；TN为两个非同类样本分别在两个簇的数量；FN为两个同类样本分别在两个簇的数量。
\qquad 评价指标选择为聚类纯度Purity、兰德系数Rand Index、F1度量值，计算公式如下：
$$Pu=\frac{聚类正确样本数}{总样本数}$$
$$RI=\frac{TP+TN}{TP+FP+FN+TN}$$
$$F1=\frac{2\ast P\ast R}{P+R}$$
\qquad 代码实现时，可以直接调用sklearn库中的pair_confusion_matrix()获得混淆矩阵，随后利用公式进行计算。具体实现代码见2.2.2实验过程（3）。

2.5 实验结果分析

\qquad 根据计算，对于鸢尾花三分类数据集，可以得到如下最好性能：

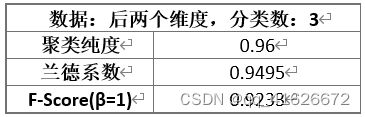
三、总结及问题说明

\qquad 本次实验的主要内容为使用K-Means算法对鸢尾花三分类数据集进行聚类操作，并计算生成模型的聚类纯度、兰德系数和F1度量值，从而对得到的模型进行评测，评价性能好坏。
\qquad 在本次实验中，未遇到很难解决的问题，得到的聚类模型性能较好，可以较准确的完成鸢尾花的聚类任务。

四、参考文献

[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.
[2] 几种常见的聚类评价指标[EB/OL]. [2022-5-3]. https://zhuanlan.zhihu.com/p/343667804.
[3] API Reference — scikit-learn 1.1.1 documentation [EB/OL]. [2022-5-3]. https://scikit-learn.org/stable/modules/classes.html.

附录：实验代码

import matplotlib.pyplot as plt  
import numpy as np  
from sklearn.cluster import KMeans
from sklearn import datasets 
from sklearn.datasets import load_iris
from sklearn.metrics import pair_confusion_matrix

iris = load_iris()
X, y = datasets.load_iris(return_X_y=True)
X = X[:, 2:] ##表示我们只取特征空间中的后两个维度
print(X.shape)
print(y.shape)

estimator = KMeans(n_clusters=3)#构造聚类器
estimator.fit(X)#聚类
label_pred = estimator.labels_ #获取聚类标签

#绘制k-means结果
x0 = X[label_pred == 0]
x1 = X[label_pred == 1]
x2 = X[label_pred == 2]
plt.scatter(x0[:, 0], x0[:, 1], c = "red", marker='o', label='label0')  
plt.scatter(x1[:, 0], x1[:, 1], c = "green", marker='*', label='label1')  
plt.scatter(x2[:, 0], x2[:, 1], c = "blue", marker='+', label='label2')  
plt.xlabel('petal length')  
plt.ylabel('petal width')  
plt.legend(loc=2)  
plt.show()  

def accuracy(labels_true, labels_pred):
    clusters = np.unique(labels_pred)
    labels_true = np.reshape(labels_true, (-1, 1))
    labels_pred = np.reshape(labels_pred, (-1, 1))
    count = []
    for c in clusters:
        idx = np.where(labels_pred == c)[0]
        labels_tmp = labels_true[idx, :].reshape(-1)
        count.append(np.bincount(labels_tmp).max())
    return np.sum(count) / labels_true.shape[0]

def get_rand_index_and_f_measure(labels_true, labels_pred, beta=1.):
    (tn, fp), (fn, tp) = pair_confusion_matrix(labels_true, labels_pred)
    ri = (tp + tn) / (tp + tn + fp + fn)
    p, r = tp / (tp + fp), tp / (tp + fn)
    f_beta = 2*p*r/(p+r)
    return ri, f_beta

y_pred = estimator.predict(X)
purity = accuracy(y, y_pred)
ri, f_beta = get_rand_index_and_f_measure(y, y_pred, beta=1.)
print(f"聚类纯度：{purity}\n兰德系数：{ri}\nF1值：{f_beta}")