机器学习实验 - 支持向量机SVM

报告内容仅供学习参考，请独立完成作业和实验喔~

一、报告摘要

1.1 实验要求

（1）掌握间隔、支持向量、对偶、核函数等概念及计算方法。
（2）基于多分类数据集，使用pandas+sklearn实现多分类预测。
（3）通过精确率、召回率和F1值度量模型性能。
（4）对比线性核和高斯核对分类性能的影响。

1.2 实验思路

\qquad 使用Python读取数据集信息并利用sklearn训练支持向量机模型，随后使用生成的支持向量机实现多分类预测，调整核函数、正则化参数、核系数等超参数，并根据精确率、召回率和F1值度量模型性能。

1.3 实验结论

\qquad 本实验通过训练使用线性核函数以及高斯核函数两种支持向量机模型，并使用GridSearchCV方法验证得到高斯核函数下最佳的C、gamma超参数，优化已训练的支持向量机模型，并通过计算精确率、召回率和F1值度量模型性能。最终使用高斯核、C=0.5、gamma=1参数的模型性能最优，其精确率为0.98125、召回率为0.98、F1值为0.98005。

二、实验内容

2.1 方法介绍

\qquad 支持向量机（Support Vector Machine, SVM）是一种监督学习方法，其基本模型是定义在特征空间上的间隔最大的线性分类器，决策边界是对学习样本求解的最大边距超平面。
\qquad 支持向量机通过引入核技巧，同时具备线性分类和非线性分类的能力。根据数据是否线性可分，支持向量机有以下几种分类：
\qquad 1) 线性可分支持向量机，对应数据线性可分，通过硬间隔最大化，学习的一个线性分类器；
\qquad 2) 线性支持向量机，对应数据近似线性可分，通过软间隔最大化，学习的一个线性分类器；
\qquad 3) 非线性支持向量机，对应数据线性不可分，通过核技巧及软间隔最大化，学习的一个非线性支持向量机。
\qquad 支持向量机中的部分概念解释及计算方法如下：
（1） 线性可分性
\qquad 给定一个数据集{(x_1, y_1),…(x_n, y_n)}，如果存在一个超平面S， 能够将数据中所有的正实例点和负实例点完全正确地划分到超平面的两侧，则称该数据线性可分。
（2） 间隔与支持向量
\qquad 在样本空间中，划分超平面可以通过以下线性方程表述：
$$w^{T}x+b=0$$
\qquad 其中$w=(w_1;w_2;\dots ;w_d)$为法向量，用于决定平面方向；为位移项，用于决定超平面与原点间距离，可以理解为相对原点上下移动的距离。
\qquad 因此，我们可以用(w,b)来定义一个超平面。同时，样本空间中任意点x到超平面(w,b)的距离可以表示为
$$r=\frac{|w^{T}x+b|}{||w||}$$
\qquad 假设现在有一个超平面可以将训练样本正确分类，即对于$(x_i,y_i)\in D$，若$y_i=+1$，有$w^{T}x+b>0$（这一类的所有点都在超平面上方）；若$y_i=-1$，有$w^{T}x+b<0$（这一类的所有点都在超平面下方）。令
$$\{\begin{array}{r}{w}^{T}x+b\ge +1,y_i=+1\\ w^{T}x+b\le -1,y_i=-1\end{array}$$

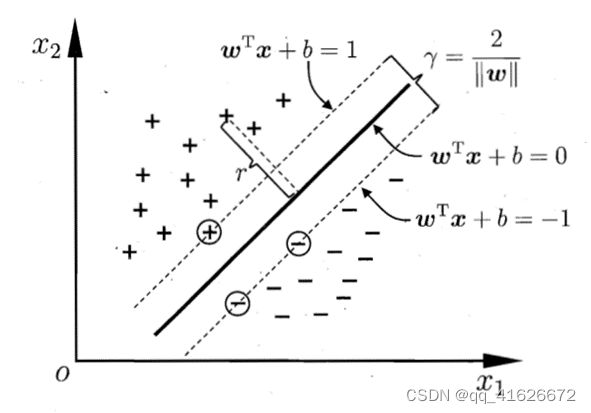
\qquad 如上图中两条虚线（均代表一个超平面），即为上方两个不等式所代表的线，线上使得不等式等号成立的点被称为支持向量（Support Vector），两个异类支持向量到超平面的距离之和为间隔（margin），计算公式如下：
$$\gamma =\frac{2}{|\left|w\right||}$$
\qquad 对于支持向量机来说，基本思路就是找到一组参数(w,b)，使得间隔γ最大，即满足如下条件：
$${min}_{w,b}=\frac{1}{2}{|\left|w\right||}^2$$
$$s.t.y_i\left(w^{T}x+b\right)\ge 1,i=1,2,\dots ,m$$
\qquad 这组公式也称为支持向量机的基本型。
（3） 对偶问题
\qquad 对偶问题是在求解支持向量机基本型时提出的一种更高效的解决办法，由基本型公式进行拉格朗日乘子法得到。具体求解过程如下即对基本型中的每条约束都添加拉格朗日乘子${\alpha }_i\ge 0$。具体的求解拉格朗日函数可写为

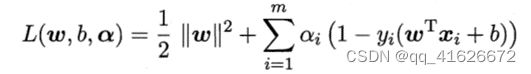
\qquad 其中$\alpha =({\alpha }_1;{\alpha }_2;\dots ;{\alpha }_m)$。令$L\left(w,b,\alpha \right)$对w和b的偏导数为0，可得

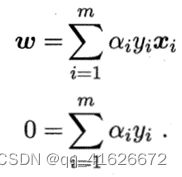
\qquad 考虑上述约束条件，同时进行代入消元，即可得到支持向量机基本型的对偶问题，公式如下：


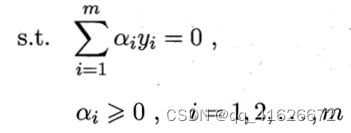
\qquad 在解出$\alpha$后，再求出w和b即可得到如下模型

$$f(x)=w^{T}x+b=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^{T}x+b$$
\qquad 在求解时，首先通过SMO等方法解出对偶问题，求得每个样本的拉格朗日乘子${\alpha }_i$。随后使取所有支持向量求解的平均值作为偏移项b的值，计算公式如下：

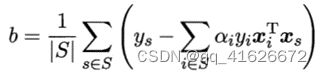
（4） 核函数
\qquad 当训练样本不满足线性可分时，我们无法按照上述计算方式找到一个超平面。但我们可以将银行本映射到一个更高维的特征空间，且对于任意有限维空间，一定存在一个高维特征空间使得样本可分。核函数正好可以实现这个低维到高维的映射过程，其定义如下：
\qquad 令$\chi$为输入空间，$Ϗ(\cdot ,\cdot )$时定义在$\chi \ast \chi$上的对称函数，则Ϗ是核函数当且仅当对于任意数据$D=x_1;x_2;\dots ;x_m$，核矩阵K总是半正定的：

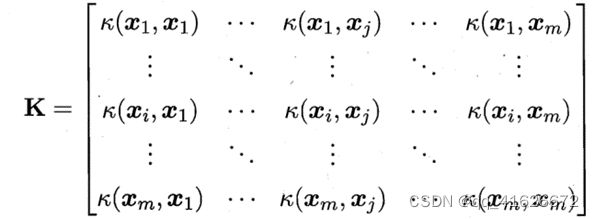
\qquad 常用核函数如下表所示：

（5） 软间隔支持向量机
\qquad 现实生活中，很难确定一个核函数使得映射到高维空间后，将不同类别的样本进行完全的划分。因此在实际应用中，引入了软间隔的概念，允许支持向量机在最大化间隔的同时，尽可能少的存在错误分类的样本。满足这种条件的支持向量机被称为软间隔支持向量机。

2.2 实验细节

2.2.1 实验环境

硬件环境：Intel® Core™ i5-10300H CPU + 16G RAM
软件环境：Windows 11 家庭中文版 + Python 3.8

2.2.2 实验过程

（1）数据集引入及分割
\qquad 将数据集按2/3训练集，1/3测试集的比例进行随机分割。

X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=1/3,random_state=0)
print('数据集样本数：{},训练样本数：{},测试集样本数：{}'.format(len(X),len(X_train),len(X_test)))

（2）训练SVM模型
\qquad 可以使用sklearn中的svm.SVC()方法训练支持向量机，其常用参数如下：
\qquad a. 正则化参数C：正浮点数，默认为1.0。用于决定正则化强度，C越大，正则化强度越低。
\qquad b. 核函数kernel：可选linear线性核、poly多项式核、rbf高斯核、sigmoid核、precomputed预计算核，以及其他可调用的核函数方法，默认为rbf高斯核。
\qquad c. 核系数gamma：浮点数，仅用于核函数为rbf、poly或sigmoid时。
\qquad 具体的训练代码及准确率如下：

# 线性核训练
linear_svm = svm.SVC(kernel='linear')
linear_svm.fit(X_train, y_train)
linear_y_pred = linear_svm.predict(X_test)
# 评估
print("精确率",precision_score(y_test, linear_y_pred, average='weighted'))
print("召回率",recall_score(y_test, linear_y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, linear_y_pred, average='weighted'))
 
# 高斯核训练
rbf_svm = svm.SVC(C=1, kernel='rbf', gamma=10)
rbf_svm.fit(X_train, y_train)
rbf_y_pred = rbf_svm.predict(X_test)
# 评估
print("精确率",precision_score(y_test, rbf_y_pred, average='weighted'))
print("召回率",recall_score(y_test, rbf_y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, rbf_y_pred, average='weighted'))

（3）利用GridSearchCV()方法寻找最优的超参数
\qquad Sklearn中提供了GridSearchCV()方法来帮助确定SVM的最优超参数。其内部实现为通过N折交叉检验依次测试每一种参数组合的可能，并根据给出的评估方式得到分数，最终根据分数从高到低排序，得到最优的超参数组合。
\qquad GridSearchCV()的常用参数如下：
\qquad a. 待估计参数模型estimator：提供一个训练得到的原始模型
\qquad b. 评价标准scoring：可以为sklearn支持的评价方式，或自己编写的函数。
\qquad c. 参数序列param_grid：以字典形式表示的需要估计参数的所有可能取值。
\qquad d. 交叉验证折数cv：默认为5折交叉验证。
\qquad 具体的代码实现过程及结果如下：

# 构造可能的函数序列，这里估计C和gamma
C_range = []
gamma_range = []
for C in range(5, 15, 1): # 0.5,0.6,......,1.4
    C_range.append(C / 10)
for gamma in range(1, 11, 1): # 1,2,......,10
    gamma_range.append(gamma)
param_grid = dict(gamma=gamma_range, C=C_range)
# 调用GridSearchCV方法，使用F1值作为评价指标，对rbf核SVM进行参数估计
grid = GridSearchCV(svm.SVC(kernel='rbf'), param_grid=param_grid, scoring="f1_weighted")
grid.fit(X, y.ravel())
print("最佳参数： %s ，F1值： %0.2f" % (grid.best_params_, grid.best_score_))

\qquad 此时我们可知，在我们给出的参数范围中，以F1值为度量指标，使用超参数C=0.5、gamma=1可得到最好的分类效果。以该超参数组合重新训练SVM模型，训练核心代码及结果如下：

new_rbf_svm = svm.SVC(C=0.5, kernel='rbf', gamma=1)
new_rbf_svm.fit(X_train, y_train)

\qquad 可以发现，与先前C=1、gamma=10时相比，此时的精确率、召回率和F1度量值均更加优秀。

2.3 实验数据介绍

\qquad 实验数据为来自UCI的鸢尾花三分类数据集Iris Plants Database。
\qquad 数据集共包含150组数据，分为3类，每类50组数据。每组数据包括4个参数和1个分类标签，4个参数分别为：萼片长度sepal length、萼片宽度sepal width、花瓣长度petal length、花瓣宽度petal width，单位均为厘米。分类标签共有三种，分别为Iris Setosa、Iris Versicolour和Iris Virginica。
\qquad 数据集格式如下图所示：

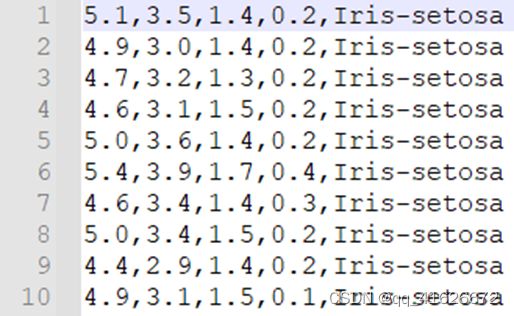
\qquad 为方便使用，也可以直接调用sklearn.datasets库中提供的load_iris()方法加载处理过的鸢尾花分类数据集。

2.4 评价指标介绍

\qquad 评价指标选择精确率P、召回率R、F1度量值F1，计算公式如下：
$$P=\frac{TP}{TP+FP}$$
$$R=\frac{TP}{TP+FN}$$
$$F1=\frac{2\ast P\ast R}{P+R}$$
\qquad 具体代码实现时，可以直接调用sklearn库中的相应方法进行计算。

2.5 实验结果分析

\qquad 根据计算，对于鸢尾花三分类数据集，可以得到如下结果：

超参数	Linear	rbf、C=1、gamma=10	rbf、C=0.5、gamma=1
精确率P	0.98125	0.93684	0.98125
召回率R	0.98	0.92	0.98
F-Score(β=1)	0.98005	0.92181	0.98005

\qquad 通过对比以上三组数据并结合相关资料可知，在调整好参数的情况下，使用高斯核的模型性能一般不会比线性核差，但由于和函数的形式更复杂，因此使用高斯核的训练速度会比线性核更慢一些。

三、总结及问题说明

\qquad 本次实验的主要内容为使用支持向量机分类鸢尾花三分类数据集，并调整参数，计算生成模型的精确度Precision、召回率Recall和F1度量值，从而对得到的模型进行评测，弄清参数与效果之间的关系，选出更优的SVM模型。
\qquad 在本次实验中，未遇到很难解决的问题，可以选出效果较好的SVM模型，完成分类任务。

四、参考文献

[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.
[2] SVM核函数的选择[EB/OL]. [2022-5-23]. https://blog.csdn.net/zhangbaoanhadoop/article/details/82083908.
[3] 1.4. Support Vector Machines — scikit-learn 1.1.1 documentation [EB/OL]. [2022-5-23]. https://scikit-learn.org/stable/modules/svm.html.
[4] sklearn.svm.SVC — scikit-learn 1.1.1 documentation [EB/OL]. [2022-5-23]. https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html.
[5] sklearn.model_selection.GridSearchCV— scikit-learn 1.1.1 documentation[EB/OL]. [2022-5-23]. https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html.

附录：实验代码

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn import svm
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
from sklearn.model_selection import GridSearchCV

iris = load_iris()
X = iris.data
y = iris.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=1/3,random_state=0)
print('数据集样本数：{},训练样本数：{},测试集样本数：{}'.format(len(X),len(X_train),len(X_test)))

# 线性核训练
linear_svm = svm.SVC(kernel='linear')
linear_svm.fit(X_train, y_train)
linear_y_pred = linear_svm.predict(X_test)
# 评估
print("精确率",precision_score(y_test, linear_y_pred, average='weighted'))
print("召回率",recall_score(y_test, linear_y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, linear_y_pred, average='weighted'))

# 高斯核训练
rbf_svm = svm.SVC(C=1, kernel='rbf', gamma=10)
rbf_svm.fit(X_train, y_train)
rbf_y_pred = rbf_svm.predict(X_test)
# 评估
print("精确率",precision_score(y_test, rbf_y_pred, average='weighted'))
print("召回率",recall_score(y_test, rbf_y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, rbf_y_pred, average='weighted'))

# 构造可能的函数序列，这里估计C核gamma
C_range = []
gamma_range = []
for C in range(5, 15, 1): # 0.5,0.6,......,1.4
    C_range.append(C / 10)
for gamma in range(1, 11, 1): # 1,2,......,10
    gamma_range.append(gamma)
param_grid = dict(gamma=gamma_range, C=C_range)
#调用GridSearchCV方法，使用F1值作为评价指标，对rbf核SVM进行参数估计
grid = GridSearchCV(svm.SVC(kernel='rbf'), param_grid=param_grid, scoring="f1_weighted")
grid.fit(X, y.ravel())
print("最佳参数： %s ，F1值： %0.2f" % (grid.best_params_, grid.best_score_))

# 优化参数后高斯核训练
new_rbf_svm = svm.SVC(C=0.5, kernel='rbf', gamma=1)
new_rbf_svm.fit(X_train, y_train)
new_rbf_y_pred = new_rbf_svm.predict(X_test)
# 评估
print("精确率",precision_score(y_test, new_rbf_y_pred, average='weighted'))
print("召回率",recall_score(y_test, new_rbf_y_pred, average='weighted'))
print("F1度量值",f1_score(y_test, new_rbf_y_pred, average='weighted'))