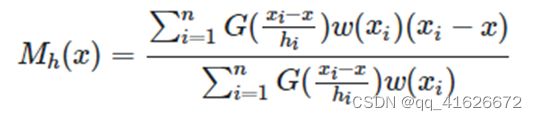机器学习实验 - MeanShift聚类
目录
-
- 一、报告摘要
-
- 1.1 实验要求
- 1.2 实验思路
- 1.3 实验结论
- 二、实验内容
-
- 2.1 方法介绍
- 2.2 实验细节
-
- 2.2.1 实验环境
- 2.2.2 实验过程
- 2.2.3 实验与理论内容的不同点
- 2.3 实验数据介绍
- 2.4 评价指标介绍
- 2.5 实验结果分析
- 三、总结及问题说明
- 四、参考文献
- 附录:实验代码
报告内容仅供学习参考,请独立完成作业和实验喔~
一、报告摘要
1.1 实验要求
(1)了解Meanshift聚类思想;
(2)编程实现Meanshift聚类算法;
(3)基于鸢尾花数据集,使用聚类纯度、兰德系数和F1值评测聚类效果。
1.2 实验思路
\qquad 使用Python编程实现Meanshift聚类算法,并对鸢尾花数据集进行聚类,同时调整参数,优化聚类效果。聚类效果根据使用聚类纯度、兰德系数和F1值评判。
1.3 实验结论
\qquad 本实验利用Python实现了Meanshift算法,并对鸢尾花数据集进行聚类。在band_width=1.3,MIN_DISTANCE=0.001的条件下,测试得到聚类纯度为0.82,兰德系数为0.82362,F1值为0.74702。
二、实验内容
2.1 方法介绍
\qquad Meanshift聚类又称为均值漂移,通过计算区域的数据密度变化,感知中心点的漂移,直到到达密度最大处。Meanshift算法是一种非参数聚类,也就是说在使用该算法进行聚类时,不需要预先设定聚类个数,这也是Meanshift与KMeans算法的最大区别。
\qquad Meanshift算法在很多领域都有成功应用,例如图像平滑、图像分割、物体跟踪等。
(1)Meanshift算法流程
\qquad Meanshift的计算过程实际上是一个不断重复迭代,直到满足条件时退出的过程。具体算法流程如下:
\qquad 1)算法初始化,将所有数据点设置为未标记状态,并随机选取一个点作为初始质心;
\qquad 2)以当前质心为圆心,半径为R画圆,将圆内点记为集合A,设置其状态簇C1,并记录样本点被访问次数;
\qquad 3)计算漂移均值向量(距离和方向),该向量由当前质心到圆内全部点的向量相加得到,容易知道该向量一定指向圆内点密度更大的位置;
\qquad 4)计算新的质心C2,并重复上述两个步骤,直到漂移距离达到阈值,更新集合A;
\qquad 5)判断上述的质心C1、C2的距离,如果小于阈值合并两个簇,数据点的次数也相应合并,不然则当做新的类别;
\qquad 6)直到所有的样本点均被访问,根据每个点对每个类的访问频率,取最大值对应的类作为该样本点所属类。
(2)Meanshift向量
\qquad 对于给定的d维空间R^n中的n个样本点 x i , i = 1 , … , n x_i,i=1,\ldots,n xi,i=1,…,n,则对于x点,其Mean shift向量的基本形式为:
M n ( x ) = 1 k ∑ x i ∈ S h ( x i − x ) M_n\left(x\right)=\frac{1}{k}\sum_{x_i\in S_h}{(x_i-x)} Mn(x)=k1xi∈Sh∑(xi−x)
\qquad 其中,S_h指的是一个半径为h的高维球区域,其定义为:
S h ( x ) = ( y ∣ ( y − x ) ( y − x ) T ≤ h 2 ) S_h\left(x\right)=(y|\left(y-x\right)\left(y-x\right)^T\le h^2) Sh(x)=(y∣(y−x)(y−x)T≤h2)
\qquad 简单来说,对于任意一个样本点,其Meanshift向量为当前样本点到以它为中心的高维球区域中全部点的向量和。如下图,我们可以直观的看到,对于密度大的方向,样本点到这个方向的向量就会越多,因此将全部向量相加后,最后的Meanshift向量一定指向这个密度最大的方向。
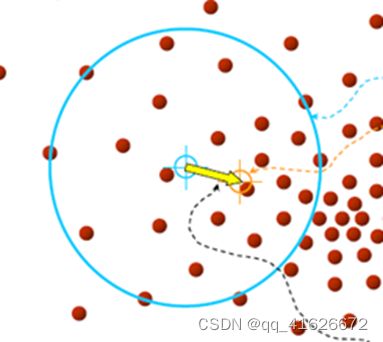
(3)核函数
\qquad 在Meanshift算法中引入核函数的目的是使得随着样本与被偏移点的距离不同,核函数是机器学习中常用的一种方式。常用的和函数有高斯核函数,计算公式如下:
G ( x ) = 1 2 π h e − x 2 2 h 2 G\left(x\right)=\frac{1}{\sqrt{2\pi}h}e^{-\frac{x^2}{2h^2}} G(x)=2πh1e−2h2x2
\qquad 其中的h为带宽(band_width),当带宽一定时,样本点之间的距离越近,和函数的值越大;当样本点之间的距离一定是,带宽越大,和函数的值越小。不同带宽下高斯核函数的图像如下图:
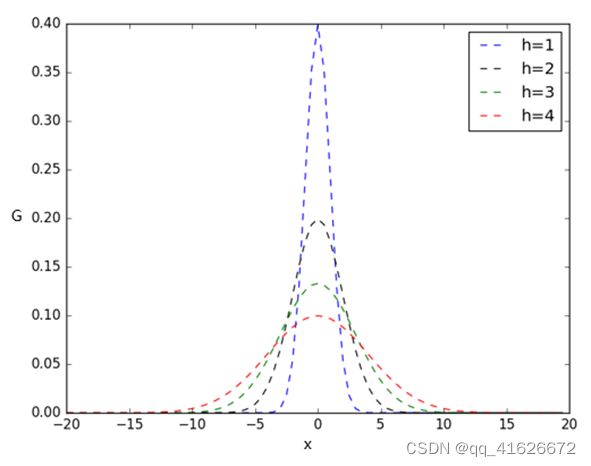
\qquad 引入高斯核函数后,可以得到如下形式的Meanshift向量:
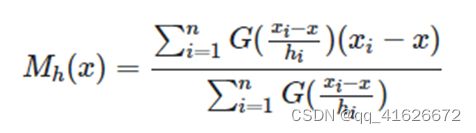
\qquad 其中 G ( x i − x h i ) G(\frac{x_i-x}{h_i}) G(hixi−x)为核函数。通常情况下, S h S_h Sh取整个数据集内全部的点。
(4)加入权重系数的Meanshift向量
\qquad 如果在计算Meanshift时考虑样本点之间距离的影响,即认为所有样本点X的重要性并不相同,在计算时可以考虑引入一个权重系数,此时Meanshift向量形式拓展为:
\qquad 其中 G ( x i − x h i ) G(\frac{x_i-x}{h_i}) G(hixi−x)为核函数, w ( x i ) w(x_i) w(xi)是不同样本点的权重。
2.2 实验细节
2.2.1 实验环境
硬件环境:Intel® Core™ i5-10300H CPU + 16G RAM
软件环境:Windows 11 家庭中文版 + Python 3.8
2.2.2 实验过程
(1)计算任意两点的欧氏距离
def euclidean_dist(pointA, pointB):
total = (pointA - pointB) * (pointA - pointB).T
return math.sqrt(total)
(2)高斯核函数
\qquad 根据高斯核函数公式 G ( x ) = 1 2 π h e − x 2 2 h 2 G\left(x\right)=\frac{1}{\sqrt{2\pi}h}e^{-\frac{x^2}{2h^2}} G(x)=2πh1e−2h2x2,编写函数如下:
def gaussian_kernel(distance, bandwidth):
m = np.shape(distance)[0] # 样本个数
right = np.mat(np.zeros((m, 1))) # 右侧矩阵
for i in range(m):
right[i, 0] = (-0.5 * distance[i] * distance[i].T) / (bandwidth * bandwidth) # -x^2/(2*h^2)
right[i, 0] = np.exp(right[i, 0]) # e
left = 1 / (bandwidth * math.sqrt(2 * math.pi)) #左侧1/√2Πh
gaussian_val = left * right
return gaussian_val
(3)计算Meanshift向量
\qquad 根据上述2.1(3)部分中引入高斯核函数后的Meanshift向量表示形式,可以编写如下的函数实现:
def shift_point(point, points, band_width): # point质心、points圆内所有点、band_width带宽
points = np.mat(points)
m = np.shape(points)[0] # 圆内样本点个数
# 计算距离
point_distances = np.mat(np.zeros((m, 1)))
for i in range(m):
point_distances[i, 0] = euclidean_dist(point, points[i])
# 计算高斯核
point_weights = gaussian_kernel(point_distances, band_width)
# 计算分母
all_sum = 0.0
for i in range(m):
all_sum += point_weights[i, 0]
# 均值偏移
point_shifted = point_weights.T * points / all_sum
return point_shifted # 新的质心
(4)迭代Meanshift向量,完成聚类
\qquad Meanshift聚类算法的核心就是将Meanshift向量不断偏移,直到找到样本圆中样本数量最多的点。因此我们的迭代过程其实就是将质心从初始点不断向偏移点移动,直到满足条件或超过阈值时退出。
\qquad 此外,在处理偏移时,对于新旧质心的处理逻辑如下:判断新旧质心的欧氏距离,如果两个质心的距离小于设定的阈值MIN_DISTANCE,此时可以看做两个类非常近,近到可以忽略,因此将这两类进行合并,看作一类;如果新旧质心的距离超过设定的阈值MIN_DISTANCE,就将这两个质心和对应的点看作两类。
\qquad 具体的实现代码如下:
def train_mean_shift(points, band_width=2): # points数据集,band_width带宽
mean_shift_points = np.mat(points) # Sh通常取全部
max_min_dist = 1
iteration = 0 # 训练迭代次数
m = np.shape(mean_shift_points)[0] # 样本的个数
need_shift = [True] * m # 默认全部需要漂移
# 计算Meanshift向量
while max_min_dist > MIN_DISTANCE:
max_min_dist = 0
iteration += 1
print("\t迭代次数:" + str(iteration))
for i in range(0, m):
# 已经用过的不再重复计算
if not need_shift[i]:
continue
p_new = mean_shift_points[i]
p_new_start = p_new # 旧质心
p_new = shift_point(p_new, points, band_width)
# 计算新质心
dist = euclidean_dist(p_new, p_new_start)
# 计算新旧质心距离
if dist > max_min_dist:
max_min_dist = dist
if dist < MIN_DISTANCE: # 过小时看作一类,不移动
need_shift[i] = False
mean_shift_points[i] = p_new
(5)样本点所属类别判断
\qquad 在Meanshift算法中,样本点的归属由各类别对其访问的频率决定,哪个类别访问样本点频率最高,样本点就归属于哪个类别。故有如下的代码实现:
def group_points(mean_shift_points):
group_assignment = []
m, n = np.shape(mean_shift_points)
index = 0
index_dict = {}
for i in range(m):
item = []
for j in range(n):
item.append(str(("%5.2f" % mean_shift_points[i, j])))
item_1 = "_".join(item)
if item_1 not in index_dict:
index_dict[item_1] = index
index += 1
for i in range(m):
item = []
for j in range(n):
item.append(str(("%5.2f" % mean_shift_points[i, j])))
item_1 = "_".join(item)
group_assignment.append(index_dict[item_1])
return group_assignment # 返回每个点的归属类别
2.2.3 实验与理论内容的不同点
\qquad 实验与理论内容的主要区别在于公式的计算方式上,比如求欧氏距离,根据理论手动计算的时候,一般是依次选择对应位置相减后求和平方相加。但在代码实现时,不会选择这种需要枚举的方式,可以直接采用矩阵与其转置矩阵相乘的方法来实现,可以大幅减少代码量,增强可读性。
\qquad 此外,虽然Meanshift是一种非参数聚类算法,但在具体使用时,仍然需要根据实验测试来确定band_width、MIN_DISTANCE等超参数的数值,才能让算法的性能更好。
2.3 实验数据介绍
\qquad 实验数据为来自UCI的鸢尾花三分类数据集Iris Plants Database。
\qquad 数据集共包含150组数据,分为3类,每类50组数据。每组数据包括4个参数和1个分类标签,4个参数分别为:萼片长度sepal length、萼片宽度sepal width、花瓣长度petal length、花瓣宽度petal width,单位均为厘米。分类标签共有三种,分别为Iris Setosa、Iris Versicolour和Iris Virginica。
\qquad 数据集格式如下图所示:
![]()
\qquad 为方便使用,也可以直接调用sklearn.datasets库中提供的load_iris()方法加载处理过的鸢尾花分类数据集。
2.4 评价指标介绍
\qquad 由于本次为聚类任务,因此使用聚类相关的混淆矩阵和评价指标。
\qquad 聚类任务中的混淆矩阵与普通混淆矩阵的意义有一定区别,如下表所示:
| 同簇 | 非同簇 | |
|---|---|---|
| 同类 | TP | FN |
| 非同类 | FP | TN |
\qquad 其中,TP为两个同类样本在同一簇的数量;FP为两个非同类样本在同一簇的数量;TN为两个非同类样本分别在两个簇的数量;FN为两个同类样本分别在两个簇的数量。
\qquad 评价指标选择为聚类纯度Purity、兰德系数Rand Index、F1度量值,计算公式如下:
P u = 聚类正确样本数 总样本数 Pu\ =\frac{聚类正确样本数}{总样本数} Pu =总样本数聚类正确样本数
R I = T P + T N T P + F P + F N + T N RI\ =\ \frac{TP+TN}{TP+FP+FN+TN} RI = TP+FP+FN+TNTP+TN
F 1 = 2 ∗ P ∗ R P + R F1\ =\ \frac{2\ast P\ast R}{P+R} F1 = P+R2∗P∗R
\qquad 代码实现时,可以直接调用sklearn库中的pair_confusion_matrix()获得混淆矩阵,随后根据公式进行计算。具体实现代码如下:
def accuracy(labels_true, labels_pred): # 计算纯度
clusters = np.unique(labels_pred)
labels_true = np.reshape(labels_true, (-1, 1))
labels_pred = np.reshape(labels_pred, (-1, 1))
count = []
for c in clusters:
idx = np.where(labels_pred == c)[0]
labels_tmp = labels_true[idx, :].reshape(-1)
count.append(np.bincount(labels_tmp).max())
return np.sum(count) / labels_true.shape[0]
def get_rand_index_and_f_measure(labels_true, labels_pred, beta=1.): # 计算兰德系数和F1值
(tn, fp), (fn, tp) = pair_confusion_matrix(labels_true, labels_pred)
ri = (tp + tn) / (tp + tn + fp + fn)
p, r = tp / (tp + fp), tp / (tp + fn)
f_beta = 2*p*r/(p+r)
return ri, f_beta
2.5 实验结果分析
\qquad 根据实验,在Iris数据集上有以下实验结果:

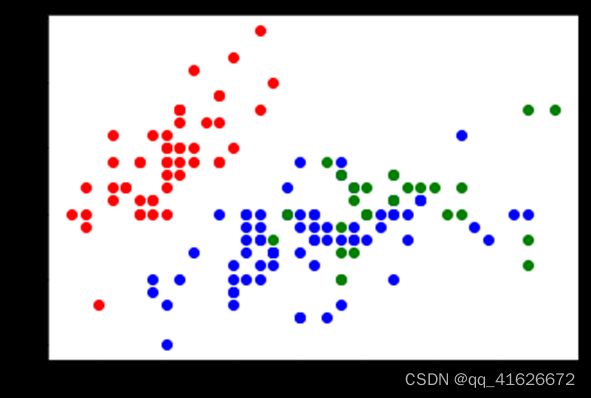
\qquad 聚类后,各点聚类结果如下图:
\qquad 根据图像可知,大部分样本被成功聚类,绿蓝两类效果稍微差一点,但红色部分样本与其余两部分样本界限较清晰。
三、总结及问题说明
\qquad 本次实验的主要内容为使用Meanshift算法对鸢尾花数据集进行聚类操作,并计算生成模型的聚类纯度、兰德系数和F1度量值,从而对得到的模型进行评测,评价性能好坏。
\qquad 在本次实验中,未遇到很难解决的问题,得到的聚类模型性能较好,可以较准确的完成鸢尾花的聚类任务。
四、参考文献
[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.
[2] 机器学习聚类算法之Mean Shift [EB/OL]. [2022-6-1]. https://www.biaodianfu.com/mean-shift.html.
[3] API Reference — scikit-learn 1.1.1 documentation [EB/OL]. [2022-6-1]. https://scikit-learn.org/stable/modules/classes.html.
附录:实验代码
import math
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.datasets import load_iris
from sklearn.metrics import pair_confusion_matrix
MIN_DISTANCE = 0.001 # 最小距离
def gaussian_kernel(distance, bandwidth): # 高斯核函数
m = np.shape(distance)[0] # 样本个数
right = np.mat(np.zeros((m, 1))) # 右侧矩阵
for i in range(m):
right[i, 0] = (-0.5 * distance[i] * distance[i].T) / (bandwidth * bandwidth) # -x^2/(2*h^2)
right[i, 0] = np.exp(right[i, 0]) # e
left = 1 / (bandwidth * math.sqrt(2 * math.pi)) #左侧1/√2Πh
gaussian_val = left * right
return gaussian_val
def shift_point(point, points, band_width): # 计算Meanshift向量
# point质心、points圆内所有点、band_width带宽
points = np.mat(points)
m = np.shape(points)[0] # 圆内样本点个数
# 计算距离
point_distances = np.mat(np.zeros((m, 1)))
for i in range(m):
point_distances[i, 0] = euclidean_dist(point, points[i])
# 计算高斯核
point_weights = gaussian_kernel(point_distances, band_width)
# 计算分母
all_sum = 0.0
for i in range(m):
all_sum += point_weights[i, 0]
# 均值偏移
point_shifted = point_weights.T * points / all_sum
return point_shifted # 新的质心
def euclidean_dist(pointA, pointB): # 欧氏距离
total = (pointA - pointB) * (pointA - pointB).T
return math.sqrt(total)
def group_points(mean_shift_points): # 判断归属类
group_assignment = []
m, n = np.shape(mean_shift_points)
index = 0
index_dict = {}
for i in range(m):
item = []
for j in range(n):
item.append(str(("%5.2f" % mean_shift_points[i, j])))
item_1 = "_".join(item)
if item_1 not in index_dict:
index_dict[item_1] = index
index += 1
for i in range(m):
item = []
for j in range(n):
item.append(str(("%5.2f" % mean_shift_points[i, j])))
item_1 = "_".join(item)
group_assignment.append(index_dict[item_1])
return group_assignment # 返回每个点的归属类别
def train_mean_shift(points, band_width=2): # Meanshift主函数
# points数据集,band_width带宽
mean_shift_points = np.mat(points) # Sh通常取全部
max_min_dist = 1
iteration = 0 # 训练迭代次数
m = np.shape(mean_shift_points)[0] # 样本的个数
need_shift = [True] * m # 默认全部需要漂移
# 计算Meanshift向量
while max_min_dist > MIN_DISTANCE:
max_min_dist = 0
iteration += 1
print("\t迭代次数:" + str(iteration))
for i in range(0, m):
# 已经用过的不再重复计算
if not need_shift[i]:
continue
p_new = mean_shift_points[i]
p_new_start = p_new # 旧质心
p_new = shift_point(p_new, points, band_width) # 计算新质心
dist = euclidean_dist(p_new, p_new_start) # 计算新旧质心距离
if dist > max_min_dist:
max_min_dist = dist
if dist < MIN_DISTANCE: # 过小时看作一类,不移动
need_shift[i] = False
mean_shift_points[i] = p_new
# 计算归属
group = group_points(mean_shift_points) # 计算所属的类别
return np.mat(points), mean_shift_points, group
def accuracy(labels_true, labels_pred): # 计算纯度
clusters = np.unique(labels_pred)
labels_true = np.reshape(labels_true, (-1, 1))
labels_pred = np.reshape(labels_pred, (-1, 1))
count = []
for c in clusters:
idx = np.where(labels_pred == c)[0]
labels_tmp = labels_true[idx, :].reshape(-1)
count.append(np.bincount(labels_tmp).max())
return np.sum(count) / labels_true.shape[0]
def get_rand_index_and_f_measure(labels_true, labels_pred, beta=1.): # 计算兰德系数和F1值
(tn, fp), (fn, tp) = pair_confusion_matrix(labels_true, labels_pred)
ri = (tp + tn) / (tp + tn + fp + fn)
p, r = tp / (tp + fp), tp / (tp + fn)
f_beta = 2*p*r/(p+r)
return ri, f_beta
# 数据处理
data=[]
X, y = datasets.load_iris(return_X_y=True)
for i in X:
data.append(list(i))
print(data[0:5])
N = len(data)
# Meanshift聚类
points, shift_points, cluster = train_mean_shift(data, 1.3)
# 绘图
data = np.array(data)
for i in range(N):
if cluster[i] == 0:
plt.plot(data[i, 0], data[i, 1], 'ro')
elif cluster[i] == 1:
plt.plot(data[i, 0], data[i, 1], 'go')
elif cluster[i] == 2:
plt.plot(data[i, 0], data[i, 1], 'bo')
# 性能指标
purity = accuracy(y, cluster)
ri, f_beta = get_rand_index_and_f_measure(y, cluster, beta=1.)
print(f"聚类纯度:{purity}\n兰德系数:{ri}\nF1值:{f_beta}")