基于倒谱法和线性预测法估计基音频率(MATLAB和Python)
基于倒谱法和线性预测法估计基音频率(MATLAB和Python)
倒谱法基音检测在python中实现
一帧信号的基音频率估计
wlen = 256
inc = 128
pitch = []
x1, Fs = librosa.load("a9.wav",sr=None)
plt.subplot(2,1,1)
# plt.plot(x1) # 画一段语音波形
signal = enframe(x1, wlen, inc)
# 取一帧
framedata = signal[15]
plt.plot(framedata)
f_b = pitch_cep(framedata, Fs)
plt.show()
一帧信号估计出来的基音频率是296.29Hz,与matlab求出的296.29Hz是一致的。
一段语音引号的基音频率估计
def pitch_cep(x, Fs):
'''
用倒谱法求基音频率
:param x: 分帧后的数据
:param Fs: 采样率
:return: f_b该帧的基音频率
'''
x2 = fftpack.fft(x)
amp = 20 * np.log10(abs(x2) + 0.0000001)
x3 = abs(fftpack.fft(amp))
x3[0:27] = 0
x3[115:256] = 0
y = max(x3)
x = x3.tolist().index(y)
f_b = Fs / (x - 1.0)
# print('基音频率:', f_b, 'Hz')
return f_b
wlen = 256
inc = 128
pitch = []
x1, Fs = librosa.load("a9.wav",sr=None)
plt.subplot(2,1,1)
plt.plot(x1)
signal = enframe(x1, wlen, inc)
# 取一帧
for i in signal:
framedata = i
f_b = pitch_cep(framedata, Fs)
pitch.append(f_b)
plt.subplot(2,1,2)
plt.plot(pitch)
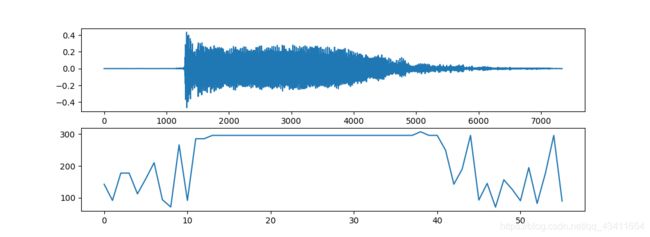
plt.show()
和MATLAB(下图)作对比,画出的结果是一致的。
LPC估计基音频率
线性预测分析是通过矩阵的特殊性质来解包含p个未知数的p个线性方程。自相关解法是的原理是在整个时间范围内使误差最小,即设 s ( n ) s(n) s(n)在 0 ⩽ n ⩽ N − 1 0 \leqslant n \leqslant N-1 0⩽n⩽N−1以外的值都是零,等同于假设了 s ( n ) s(n) s(n)经过了有限长度的矩形窗、海宁窗或者汉宁窗,就可以用p个方程来解有p个未知数的方程组了。
通常 s ( n ) s(n) s(n)的加窗自相关函数定义为:
r ( j ) = ∑ n = 0 N − 1 s ( n ) s ( n − j ) , ( 1 ⩽ j ⩽ p ) (1) r(j)=\sum_{n=0}^{N-1}s(n)s(n-j),(1\leqslant j \leqslant p) \tag1 r(j)=n=0∑N−1s(n)s(n−j),(1⩽j⩽p)(1)
由于 ϕ ( j , i ) \phi(j,i) ϕ(j,i)等效于 r ( j − i ) r(j-i) r(j−i),由于自相关是偶函数,所以有:
ϕ ( j , i ) = r ( ∣ j − i ∣ ) (2) \phi(j,i)=r(|j-i|) \tag2 ϕ(j,i)=r(∣j−i∣)(2)
因此式
φ ( j , 0 ) = ∑ i = 1 p a i φ ( j , i ) , ( 1 ⩽ j ⩽ p ) (3) \varphi(j,0)=\sum_{i=1}^{p}a_i\varphi(j,i),(1\leqslant j \leqslant p)\tag3 φ(j,0)=i=1∑paiφ(j,i),(1⩽j⩽p)(3)
可以表示为:
r ( j ) = ∑ i = 1 p a i r ( ∣ j − i ∣ ) , ( 1 ⩽ j ⩽ p ) (4) r(j)=\sum_{i=1}^pa_ir(|j-i|),(1\leqslant j \leqslant p) \tag4 r(j)=i=1∑pair(∣j−i∣),(1⩽j⩽p)(4)
最小均方误差改写为:
E = r ( 0 ) − ∑ i = 1 p a i r ( i ) (5) E=r(0)-\sum_{i=1}^{p}a_ir(i) \tag5 E=r(0)−i=1∑pair(i)(5)
展开式(5)可得到方程组:
[ r ( 0 ) r ( 1 ) r ( 2 ) . . . r ( p − 1 ) r ( 1 ) r ( 0 ) r ( 1 ) . . . r ( p − 2 ) r ( 2 ) r ( 1 ) r ( 0 ) . . . r ( p − 3 ) . . . . . . . . . . . . . . . r ( p − 1 ) r ( p − 2 ) r ( p − 3 ) . . . r ( 0 ) ] [ a 1 a 2 a 3 . . . a p ] = [ r ( 1 ) r ( 2 ) r ( 3 ) . . . r ( p ) ] (6) \begin{bmatrix}r(0)&r(1)&r(2)&...&r(p-1)\\r(1)&r(0)&r(1)&...&r(p-2)\\r(2)&r(1)&r(0)&...&r(p-3)\\...&...&...&...&...\\r(p-1)&r(p-2)&r(p-3)&...&r(0)\end{bmatrix}\begin{bmatrix}a_1\\a_2\\a_3\\...\\a_p\end{bmatrix}=\begin{bmatrix}r(1)\\r(2)\\r(3)\\...\\r(p)\end{bmatrix} \tag6 ⎣⎢⎢⎢⎢⎡r(0)r(1)r(2)...r(p−1)r(1)r(0)r(1)...r(p−2)r(2)r(1)r(0)...r(p−3)...............r(p−1)r(p−2)r(p−3)...r(0)⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎢⎡a1a2a3...ap⎦⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎡r(1)r(2)r(3)...r(p)⎦⎥⎥⎥⎥⎤(6)
其中左边为相关函数的矩阵,以对角线为对称,其主对角线以及和主对角线平行的任何一条斜线上所有的元素相等。这种矩阵称为托普利兹(Toepliz)矩阵,而这种方程称为Yule-Walker方程。这种矩阵方程采用递归方法求解,基本思想就是递归解法分布进行,常用的是莱文逊-杜宾(Levinson - Durbin)算法。
该算法的计算过程为:
- 当 i = 0 i=0 i=0时, E 0 = r ( 0 ) E_0=r(0) E0=r(0), a 0 = 1 a_0=1 a0=1;
- 对于第 i i i次递归 ( i = 1 , 2 , … , p ) (i=1,2,\dots,p) (i=1,2,…,p)
k i = 1 E i − 1 [ r ( i ) − ∑ j = 1 i − 1 a j i − 1 r ( j − i ) ] (7) k_i=\frac{1}{E_{i-1}}[r(i)-\sum_{j=1}^{i-1}a_j^{i-1}r(j-i)] \tag7 ki=Ei−11[r(i)−j=1∑i−1aji−1r(j−i)](7)
i a i ( i ) = k i (8) ia_i^{(i)}=k_i \tag8 iai(i)=ki(8)
对于 j = 1 到 i − 1 j=1到i-1 j=1到i−1
a j ( i ) = a j ( i − 1 ) − a i − j ( i − 1 ) (9) a_j^{(i)}=a_j^{(i-1)}-a_{i-j}^{(i-1)} \tag9 aj(i)=aj(i−1)−ai−j(i−1)(9)
E i = ( i − k i 2 ) E i − 1 (9) E_i=(i-k_i^2)E_{i-1} \tag9 Ei=(i−ki2)Ei−1(9)
- 增益 G G G为
G = E p G=\sqrt{E_p} G=Ep
- 递归得到
E p = r ( 0 ) ∏ i = 1 p ( 1 − k i 2 ) E_p=r(0)\prod_{i=1}^p(1-k_i^2) Ep=r(0)i=1∏p(1−ki2)
Matlab一帧语音的基音频率
估计一帧语音的基音频率
matlab中有lpc函数直接可以调用,因此在python中编写算法去计算,利用matlab中的lpc函数来验证算法的正确性。
%用LPC法计算基音频率
clc; close all; clear all;
[x1,Fs] = audioread('voice/a9.wav');
wlen=256; inc=128; % 给出帧长和帧移
N=length(x1); % 信号长度
time=(0:N-1)/Fs; % 计算出信号的时间刻度
signal=enframe(x1,wlen,inc)'; % 分帧
framedata = signal(:,15);
subplot(2,1,1)
plot(framedata);
%LPC
[x3,r]=lpc(framedata,256);
x3=abs(x3);
x3(1:27) = 0;%在话音基频范围外的都取零
x3(115:256) = 0;
[M,idx] = max(x3);
subplot(2,1,2);
plot(x3);
f_b=Fs/(idx-1);
所求出的基音频率是285.71Hz
估计一段语音的基音频率
%求出一段语音的基音频率
clc; close all; clear all;
[x1,Fs] = audioread('voice/a9.wav');
subplot(2,1,1);
plot(x1);
wlen=256; inc=128; % 给出帧长和帧移
N=length(x1); % 信号长度
time=(0:N-1)/Fs; % 计算出信号的时间刻度
signal=enframe(x1,wlen,inc)'; % 分帧
[n,m]=size(signal);
for i=1:m
framedata = signal(:,i);
% f_b=pitch_cep(framedata,Fs); %倒谱法
% f_b=pitch_cor(framedata,Fs); %自相关法
% f_b=pitch_admf(framedata,Fs); %平均幅度差
f_b=pitch_lpc(framedata,Fs); %LPC
x(i)=f_b;
end
subplot(2,1,2);
plot(x);
python实现
估计一帧语音的基音频率
def pitch_lpc(s, p):
'''
此函数用LPC法求基音频率
:param s: 一帧数据
:param p: 预测阶数
:return: ar:预测系数
'''
n = len(s)
# 计算自相关函数
Rp = np.zeros(p) #创建0矩阵
for i in range(p):
Rp[i] = np.sum(np.multiply(s[i + 1:n], s[:n - i - 1]))
Rp0 = np.matmul(s, s.T)
Ep = np.zeros((p, 1))
k = np.zeros((p, 1))
a = np.zeros((p, p))
# 处理i=0的情况
Ep0 = Rp0
k[0] = Rp[0] / Rp0
a[0, 0] = k[0]
Ep[0] = (1 - k[0] * k[0]) * Ep0
# i=1开始,递归计算
if p > 1:
for i in range(1, p):
k[i] = (Rp[i] - np.sum(np.multiply(a[:i, i - 1], Rp[i - 1::-1]))) / Ep[i - 1]
a[i, i] = k[i]
Ep[i] = (1 - k[i] * k[i]) * Ep[i - 1]
for j in range(i - 1, -1, -1):
a[j, i] = a[j, i - 1] - k[i] * a[i - j - 1, i - 1]
ar = np.zeros(p + 1)
ar[0] = 1
ar[1:] = -a[:, p - 1]
G = np.sqrt(Ep[p - 1])
return ar, G
wlen = 256
inc = 128
pitch = []
x1, Fs = librosa.load("a9.wav",sr=None)
# plt.plot(x1) # 画一段语音波形
signal = enframe(x1, wlen, inc)
# 取一帧
framedata = signal[15]
ar, G = pitch_lpc(framedata, p=256)
ar = abs(ar)
ar[0:27] = 0
ar[115:257] = 0
y = max(ar)
x = ar.tolist().index(y)
f_b = Fs / x
print('x坐标:\n', x)
print('基音频率:\n', f_b)
plt.plot(ar)
plt.plot(x, y, 'r')
所求出的基音频率是296.29Hz,与matlab求出的有10Hz左右的差距

估计一段语音的基音频率
def pitch_lpc(s, p):
'''
此函数用LPC法求基音频率
:param s: 一帧数据
:param p: 预测阶数
:return: ar:预测系数
'''
n = len(s)
# 计算自相关函数
Rp = np.zeros(p) # 给一个预测阶数的零矩阵
for i in range(p): # 求自相关
Rp[i] = np.sum(np.multiply(s[i + 1:n], s[:n - i - 1]))
Rp0 = np.matmul(s, s.T)
Ep = np.zeros((p, 1))
k = np.zeros((p, 1))
a = np.zeros((p, p))
# 处理i=0的情况
Ep0 = Rp0
k[0] = Rp[0] / Rp0
a[0, 0] = k[0]
Ep[0] = (1 - k[0] * k[0]) * Ep0
# i=1开始,递归计算
if p > 1:
for i in range(1, p):
k[i] = (Rp[i] - np.sum(np.multiply(a[:i, i - 1], Rp[i - 1::-1]))) / Ep[i - 1]
a[i, i] = k[i]
Ep[i] = (1 - k[i] * k[i]) * Ep[i - 1]
for j in range(i - 1, -1, -1):
a[j, i] = a[j, i - 1] - k[i] * a[i - j - 1, i - 1]
ar = np.zeros(p + 1)
ar[0] = 1
ar[1:] = -a[:, p - 1] # 求得预测系数
G = np.sqrt(Ep[p - 1]) # 得到递归增益G
ar = abs(ar)
ar[0:27] = 0 #将话音范围外置零
ar[115:257] = 0
y = max(ar) #找最大值
x = ar.tolist().index(y) #找到最大值对应的坐标
print('Fs=',Fs)
print("x:",x)
f_b = Fs / (x) # 计算基频
return f_b
wlen = 256
inc = 128
pitch = []
x1, Fs = librosa.load("a9.wav", sr=None)
plt.subplot(2,1,1)
plt.plot(x1) # 画一段语音波形
signal = enframe(x1, wlen, inc)
# 求一段语音pitch用
for i in signal:
framedata = i
f_b = pitch_lpc(framedata, 256)
pitch.append(f_b)
plt.subplot(2,1,2)
plt.plot(pitch)
plt.show()
与MATLAB画出的统一语音的基音频率相比,两个图基本是一致的。