Keras深度学习入门篇
Keras深度学习入门篇
第一部分:机器学习基础
一、机器学习的四个分支
- 监督学习
- 分类
- 回归
- 序列生成,给定一张图像,预测描述图像的文字
- 语法树预测,给定一个句子,预测其分解生成的语法树
- 目标检测,给定一张图像,在图中特定目标的周围画上一个边界框
- 图像分割,给定一张图像,在特定物体上画一个像素级的掩模
- 无监督学习
常用于数据可视化、数据压缩、数据去噪或者更好的理解数据中的相关性
- 降维
- 聚类
- 自监督学习
没有人工标注标签的监督学习,比如根据给定文本中前面的词来预测下一个词 - 强化学习
接收环境信息,并学会选择使某种奖励最大化,如下围棋
二、张量(Tensor)是什么?
张量是矩阵向任意维度的推广,是N维数组,能张能缩的变量。
张量的三个关键属性
1)维度、轴的个数、阶, ndim
2)形状, shape。
3)数据类型,dtype
通常,只有数字张量,没有字符张量,因为张量存储在预先分配的连续内存段中,而字符串的长度是可变的,无法用这种方式存储
- 标量(0D 张量, scalar,也叫标量张量、零维张量)
>>> import numpy as np
>>> x = np.array(13)
>>> x
array(13)
>>> x.ndim
0
- 向量(1D 张量, vector,一维张量)
>>> x = np.array([12, 3, 6, 14, 7])
>>> x
array([12, 3, 6, 14, 7])
>>> x.ndim
1
- 矩阵(2D 张量,matrix)
>>> x = np.array([[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]])
>>> x.ndim
2
向量数据: 2D 张量,形状为 (samples, features)
比如,人口统计数据集,其中包括每个人的年龄、邮编和收入。每个人可以表示为包含 3 个值的向量,而整个数据集包含 100000 个人,因此可以存储在形状为 (100000, 3) 的 2D张量中
- 3D 张量
>>> x = np.array([[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]],
[[5, 78, 2, 34, 0],
[6, 79, 3, 35, 1],
[7, 80, 4, 36, 2]]])
>>> x.ndim
3
时间序列数据或序列数据: 3D 张量,形状为 (samples, timesteps, features)
比如,股票价格数据集,每一分钟,我们将股票的当前价格、前一分钟的最高价格、最低价格保存为一个 3D 向量,整个交易日的数据为 (390, 3) 的 2D 张量(一个交易日有 390 分钟),250 天的数据则可以保存为 (250, 390, 3) 的 3D 张量
-
4D 张量
形状为 (samples, height, width, channels) 或 (samples, channels, height, width)
比如,128张照片(256*256px)的彩色照片可以表示为(128, 256, 256, 3); -
5D 张量
形状为 (samples, frames, height, width, channels) 或 (samples, frames, channels, height, width)
比如,一个以每秒 4 帧采样的 60 秒 YouTube 视频片段,视频尺寸为 144× 256,共有 240 帧, 4 个这样的视频片段组成的批量将保存在形状为 (4, 240, 144, 256, 3)的张量中
三、张量的运算(参考矩阵运算)
- 逐元素运算,如,加减法,one by one 对齐齐
- 广播,维度不够,重复使用来凑,如,矩阵加一个常数中的常数
- 点积,如,矩阵乘法
- 变形,如转置
四、通用工作流程
-
- 定义问题
有哪些数据可用? 你想要预测什么? 你是否需要收集更多数据或雇人为数据集手动添加标签?
-
- 找到能够可靠评估目标成功的方法
对于简单任务,可以用预测精度,但很多情况都需要与领域相关的复杂指标
-
- 准备用于评估模型的验证过程
训练集、验证集和测试集是必须定义的。验证集和测试集的标签不应该泄漏到训练数据中
-
- 数据向量化
方法是将数据转换为向量并预处理,使其更容易被神经网络所处理(数据标准化等)
-
- 开发第一个模型
它要打败基于常识的简单基准方法,从而表明机器学习能够解决你的问题。事实上并非总是如此!
-
- 通过调节超参数和添加正则化来逐步改进模型架构
仅根据模型在验证集(不是测试集或训练集)上的性能来进行更改。请记住,你应该先让模型过拟合(从而找到比你的需求更大的模型容量),然后才开始添加正则化或降低模型尺寸
-
- 调节超参数时要小心验证集过拟合
超参数可能会过于针对验证集而优化。我们保留一个单独的测试集,正是为了避免这个问题!
第二部分:深度学习基础
一、深度学习过程
想象有两张彩纸:一张红色,一张蓝色,将其中一张纸放在另一张上,揉成小球。这个皱巴巴的纸球就是你的输入数据,每张纸对应于分类问题中的一个类别。深度学习,就是通过一序列的的变换来一点点展开小球。
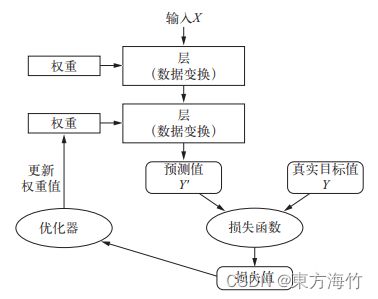
(1) 抽取训练样本 x 和对应目标y组成的数据批量
(2) 在x上运行网络,得到预测值y_pred
(3) 计算网络在这批数据上的损失,用于衡量y_pred和y之间的距离
(4) 计算损失相对于网络参数的梯度[一次反向传播(backward pass)]
(5) 将参数沿着梯度的反方向移动一点,比如 W -= step * gradient,从而使这批数据上的损失减小一点
二、层(level)
多个层组合成网络(或模型),常用的层有:
- 全连接层( fully connected layer),也叫密集连接层(densely connected layer)、密集层(dense layer)
- 循环层( recurrent layer,比如 Keras 的 LSTM 层)通常来处理形状为 (samples, timesteps, features) 的 3D 张量序列数据
- 卷积层( Keras 的 Conv2D),通常用来处理保存在 4D 张量中的图像数据
多层组成的网络结构可分为:
- 串行网络
- 双分支( two-branch)网络
- 多头( multihead)网络
- Inception 模块
选择正确的网络架构更像是一门艺术
三、损失函数( loss function)
用于学习的反馈信号,衡量在训练数据上的性能,在训练过程中需要将其最小化。它能够衡量当前任务是否已成功完成。
四、优化器( optimizer)
决定学习过程如何进行,决定如何基于损失函数对网络进行更新,它执行的是随机梯度下降( SGD)的某个变体。
- 梯度
梯度( gradient)是张量运算的导数,它是导数向多元函数导数的推广
y_pred = dot(W, x)
loss_value = loss(y_pred, y)
//如果输入数据x和y保持不变,那么这可以看作将W映射到损失值的函数
loss_value = f(W)
gradient(f)(W0)是函数f(W)在W0的导数
对于张量的函数 f(W),你可以通过将W向梯度的反方向移动来减小f(W),
比如 W1 = W0 - step * gradient(f)(W0),其中 step 是一个很小的比例因子。(注意,比例因子step是必需的,因为gradient(f)(W0) 只是W0附近曲率的近似值,不能离W0太远)于是还会有W2、W3、、直至收敛
-
随机梯度下降可分为
每次迭代取小批量的数据 —— 小批量SGD
每次迭代取一个数据 —— 真SGD
每一次迭代都在所有数据上运行 —— 批量SGD -
SGD 还有多种变体
优化点在于计算下一次权重更新时还考虑了上一次的权重更新,比如带动量的SGD、 Adagrad、RMSProp等变体。这些变体被称为优化方法( optimization method)或优化器( optimizer)。
动量的概念源自物理学,动量解决了 SGD 的两个问题:收敛速度和局部极小点。动量方法的实现过程是每一步移动小球,不仅要考虑当前的斜率值(加速度),还要考虑当前的速度(来自于之前的加速度)。在实践中指的是,更新参数 w 不仅要考虑当前的梯度值,还要考虑上一次的梯度值 -
反向传播( backpropagation,有时也叫反式微分, reverse-mode differentiation)
将链式法则应用于神经网络梯度值的计算,得到的算法叫作反向传播。反向传播从最终损失值开始,从最顶层反向作用至最底层,利用链式法则计算每个参数对损失值的贡献大小
五、监控指标(metric)
在训练和测试过程中需要监控的指标,常见的指标,比如准确率
-
Accuracy metrics
- Accuracy
- BinaryAccuracy
- CategoricalAccuracy
- TopKCategoricalAccuracy
- SparseTopKCategoricalAccuracy
-
Probabilistic metrics
- BinaryCrossentropy
- CategoricalCrossentropy
- SparseCategoricalCrossentropy
- KLDivergence
- Poisson
-
Regression metrics
- MeanSquaredError
- RootMeanSquaredError
- MeanAbsoluteError
- MeanAbsolutePercentageError
- MeanSquaredLogarithmicError
- CosineSimilarity
- LogCoshError
-
Classification metrics based on True/False positives & negatives
- AUC
- Precision
- Recall
- TruePositives
- TrueNegatives
- FalsePositives
- FalseNegatives
- PrecisionAtRecall
- SensitivityAtSpecificity
- SpecificityAtSensitivity
-
Image segmentation metrics
- MeanIoU
-
Hinge metrics for "maximum-margin"ification
- Hinge
- SquaredHinge
- CategoricalHinge
第三部分:Keras基础
一、Keras是什么?
Keras 是一个模型级( model-level)的Python深度学习框架
keras可以方便地定义和训练几乎所有类型的深度学习模型,具有以下重要特性:
- 相同的代码可以在CPU或GPU上无缝切换运行
- 具有用户友好的API,便于快速开发深度学习模型的原型
- 内置支持卷积网络(用于计算机视觉)、循环网络(用于序列处理)以及二者的任意
组合 - 支持任意网络架构:多输入或多输出模型、层共享、模型共享等。这也就是说, Keras
能够构建任意深度学习模型,无论是生成式对抗网络还是神经图灵机
二、Keras和Tensorflow有什么关系?
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Qvacvrkd-1669885429458)(…/pic/deep-learning/keras.png)]
- keras提供了一个高层次的构建模块
- Keras 有三个后端实现方式: TensorFlow、Theano、微软认知工具包( CNTK, Microsoft cognitive toolkit)
- NVIDIA CUDA 深度神经网络库( cuDNN),是 在 GPU 上,TensorFlow封装的一个高度优化的深度学习运算库
- Eigen,是TensorFlow封装的一个低层次的张量运算库
三、Keras的开发步骤
- 定义训练数据:输入张量和目标张量
- 定义层组成的网络(或模型),将输入映射到目标
- 配置学习过程:选择优化器、损失函数、监控指标
- 调用模型的 fit 方法在训练数据上进行迭代
from keras import models
from keras import layers
from keras import optimizers
# 创建方式1
model = models.Sequential()
model.add(layers.Dense(32, activation='relu', input_shape=(784,)))
model.add(layers.Dense(10, activation='softmax'))
model.compile(optimizer=optimizers.RMSprop(lr=0.001),
loss='mse',
metrics=['accuracy'])
model.fit(input_tensor, target_tensor, batch_size=128, epochs=10)
# 创建方式2
# 下面是用函数式 API 定义的相同模型。
input_tensor = layers.Input(shape=(784,))
x = layers.Dense(32, activation='relu')(input_tensor)
output_tensor = layers.Dense(10, activation='softmax')(x)
model = models.Model(inputs=input_tensor, outputs=output_tensor)
第四部分:Quickly Start
一、四份常见的数据实践
| Case场景 | 数据 | 数据结构(x.shape, y.shape) | 网络结构 | 优化器 | 损失函数 | 监控指标 |
|---|---|---|---|---|---|---|
| 多分类 | MNIST手写字识别 | train: (60000, 28, 28) (60000,) test: (10000, 28, 28) (10000,) |
(512, activation=‘relu’, input_shape=(28 * 28,)) (10, activation=‘softmax’) |
rmsprop | categorical_crossentropy | accuracy |
| 二分类 | 电影评论IMDB | train: (25000,) (25000,) test: (25000,) (25000,) |
(16, activation=‘relu’, input_shape=(10000,)) (16, activation=‘relu’) (1, activation=‘sigmoid’) |
rmsprop | 二元交叉熵binary_crossentropy | accuracy |
| 多分类 | 新闻分类 | train: (8982,) (8982,) test: (2246,) (2246,) |
(64, activation=‘relu’, input_shape=(10000,)) (64, activation=‘relu’) (46, activation=‘softmax’) |
rmsprop | 分类交叉熵categorical_crossentropy | accuracy |
| 回归问题 | 房价预测 | train: (404, 13) (404,) test: (102, 13) (102,) |
(64, activation=‘relu’, input_shape=(13,) (64, activation=‘relu’) (1) |
rmsprop | 均方误差mse | mae |
二、过拟合,泛化能力不强
- 最优的解决办法是获取更多的训练数据
- 减小网络大小
- 添加权重正则化
- 添加dropout正则化
在训练过程中随机将该层的一些输出特征舍弃(设置为0),在层的输出值中引入噪声,打破不显著的偶然模式
三、欠拟合,模型能力不强
- 添加更多的层
- 让每一层更大
- 训练更多的轮次
参考文章&图书
Keras文档
Keras中文文档
TensorFlow中文官网
《Python深度学习》
@ 学必求其心得,业必贵其专精