强化学习原理与应用作业二

0. 说明

为避免杂乱，对Task2第三问CartPole-v0的A2C、Task3的两个TD3，这三个任务分别建立单独的.py文件 (A2C_CartPole_v0.py、TD3_BipedalWalker.py、TD3_LunarLanderContinuous.py)编写实现，直接单独运行，不依赖作业提供的框架；对其余任务，在提供的框架上编写。

所有代码代码已设置为测试模式，即载入训练的模型进行测试，所有路径为相对路径可以直接运行。

1. Task 1 Implementing DQN

Nature DQN、Double DQN和Dueling DQN间的关系在下文的“个人理解”部分给出，这里仅给出训练曲线(对Dueling DQN具体用的是D3QN)。由于该环境训练较久（涉及对图片的卷积操作提取特征），这里并没有取不同的随机种子多次实验来判断算法的稳定性，且episodes的总数取值较小。

1.1 DQN for PongNoFrameskip-v4

探索概率epsilon的最小值分别设置为0.1、0.01（这里设置episolon会在前100episodes指数级递减为最小值），学习曲线如下图：


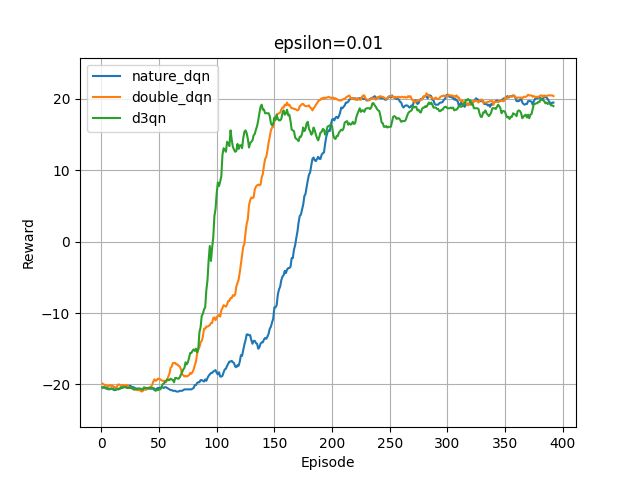
从这两图中及其他的实验结果，有三条发现：

1. 可以看到较小的epsilon有助于DQN算法快速收敛，并且训练更加稳定、训练后期的回合奖励波动较小。
2. 尽管epsilon取值0.1时（第一张图），训练收敛后的累积回报远小于20，但测试时其累积奖励能达到最优的20-21。因为训练时，在后期epsilon始终为0.1，随机动作的概率仍较大，会偏离策略网络的输出动作导致累积奖励偏小，但测试时不会使用0.1概率的随机动作仅贪心选择最优动作，即测试时的累积奖励不再受epsilon随机动作的影响。
3. 从图中可以发现，就收敛速度而言，D3QN > Double DQN > Nature DQN，但就训练后期的稳定性以及最优性而言，却是Double DQN > Nature DQN > D3QN。造成不一致的原因可以是多样的：首先，相同的算法对不同的环境的适用情况不一样，不可能存在某一算法在任何环境下都优于另一算法，即在某些环境下，普通的Nature DQN的表现优于Double DQN或Double DQN优于D3QN是非常正常且常见的；其次，对同一环境，不同算法的最优超参数大概率不一样（尽管实验中的三算法都属于DQN系列），而实验中为求方便，参数都设置的相同，例如隐藏层都是128个神经元，学习率都为3e-4。这些可能导致一些误差。

2. Task 2 Implementing Policy Gradient

2.1 REINFORCE及变体 for CartPole-v0

对REINFORCE算法，其目标是最大化累积折扣奖励，目标梯度为：
$$\nabla J_{\theta }(\theta )={\mathbb{E}}_{{\pi }_{\theta }}[{\nabla }_{\theta }log{\pi }_{\theta }(s,a)Q(s,a)]$$其本质是，在当前时刻t，$G_t$ 或$Q(s,a)$大于0，则增大概率$\pi (s,a)$。故为让算法更好的收敛，需要让$G_t$ 有正有负。具体的实现中，对$G_t$ 减去均值后再除以标准差，即进行标准化让其有正有负（类似以均值作为基线）。
REINFORCE的改进版本，对$G_t$ 或$Q(s,a)$减去一个常数项，使其方差更小进而更容易训练与收敛。其目标梯度为：
$$\nabla J_{\theta }(\theta )={\mathbb{E}}_{{\pi }_{\theta }}[{\nabla }_{\theta }log{\pi }_{\theta }(s,a)(Q(s,a)-b(s))]$$从上式可以看到，$(Q(s,a)-b(s))$在更新策略网络${\pi }_{\theta }$的过程中是一个常数项，与策略网络的参数$\theta$无关，并且常数在优化的过程中会被学习率吸收，不会影响梯度。

对朴素的REINFORCE和REINFORCE with baseline两种算法分别在四个不同的随机种子 (1、2、3、4)下进行实验，绘制的学习曲线如下所示。可以看到，带基线的REINFORCE在训练后期更稳定。

2.2 A2C for CartPole-v0

与REINFORCE用蒙特卡洛采样轨迹获得当前状态动作价值函数$Q(s,a)$不同的是，A2C使用状态价值函数$V(s)$，进而间接得到当前状态的动作价值函数：
$$Q(s_t,a_t)=r(s_t,a_t)+\gamma V(s_{t+1})$$
实验发现，在CartPole-v0环境下，A2C算法十分不稳定，对多数超参数都很敏感，这里仔细调参，并训练448个episodes后停止，因为继续训练模型会退化崩塌，具体参数见A2C_CartPole_v0.py开头的parse部分。
训练曲线及测试效果如下。

3. Task 3 Implementing DDPG (TD3)

3.1 DDPG与TD3

DDPG是一种AC结构，共有4个网络，分别是当前Actor、目标Actor、当前Critic、目标Critic。在实际使用中，DDPG已经被性能更优的TD3所代替，相比于DDPG(Deep Deterministic Policy Gradient)，TD3(Twin Delayed Deep Deterministic Policy Gradient)有3处改进：

1. Twin Q networks
   即TD3的首字母T，与Double DQN的思想一致 (但Double DQN并没有显式地使用两个目标Q网络和两个当前Q网络)，TD3中使用两个当前Critic网络、两个目标Critic网络来减缓高估问题。具体地，一般采用两个孪生网络的最小者或均值作为最终Q值来减缓高估。这样一来，TD3共有6个网络：当前Actor、目标Actor、当前Critic2(twin)、目标Critic2(twin)。
2. 延迟更新
   即TD3中的第一个D，Delayed，即更新Actor网络和目标网络的频率小于Critic网络。由于Actor网络和Critic网络存在相互依赖的关系，当评价网络Critic存在较大误差时，肯定不能准确地指引Actor网络的更新。延迟更新的思想就是多次更新当前Critic网络后才更新一次Actor网络，希望Critic更加准确后再来指引Actor的更新。
3. 使用探索噪声与策略噪声
   在Actor网络输出一个确定性的动作$u_{\theta }(s)$后，并不直接使用该动作，而是在$u_{\theta }(s)$上加上0均值的探索噪声并clip到合法区间；在计算目标$Q(s_{t+1},a_{t+1})$时，下一时刻的动作也添加策略，希望训练更新平滑、稳定。

3.2 TD3 for LunarLanderContinuous-v2

下面两图分别是探索噪声取0.1和0.01是对应的学习曲线，可以发现，探索噪声稍大时，会收敛更快，但波动较大，即不稳定。


测试效果如下：

3.3 TD3 for BipedalWalker-v2

训练曲线及测试结果如下。

---

4. 个人理解

4.1 Q Learning到DQN

DQN是对表格型的Q Learning的扩展。Q Learing的核心是维护Q(s,a)这样的二维表，但当求解问题的状态空间S无穷多时，Q learning将不再有效，因为此时Q表的行数无穷大，无论是存储Q表还是更新Q表都不再可行。

DQN就是为了解决状态空间S高维或连续的问题。DQN使用神经网络来处理不同的状态，正如一个函数的输入可以是整个自变量的定义域。具体地，有两种实现，一种直接将s和a拼接起来输入神经网络，输出为一维的Q(s,a)，另一种以s作为神经网络的输入，输出各个动作在该状态下的Q值，即输出|A|维。

4.2 DQN的各种版本

Naive DQN是最原始的DQN，对四元组(s, a, r, s’)，其目标Q值的计算如下：
$$target\_q=r+\gamma \ast (1-mask)\ast \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })$$
Nature DQN引入了目标网络用于解决Naive DQN中存在的自举问题。“自举”，字面意思就是自己举自己，形象地描述了循环依赖的关系。在Naive DQN中，计算目标Q值时用到Q网络，而更新Q网络（参数）时又用到目标Q值，两者相互依赖，不利于Q网络收敛。为此，Nature DQN使用目标网络来拟合下一时刻状态s’对应的Q值，其目标Q值的计算如下：
$$target\_q=r+\gamma \ast (1-mask)\ast \underset{a^{\prime }}{\max }{Q}_{target}(s^{\prime },a^{\prime })$$目标Q网络的网络参数不需要迭代更新，而是每隔一段时间从当前Q网络Q复制过来（硬更新，区别策略梯度方法常用的软更新），即延时更新，这样可以减少目标Q值和当前的Q值相关性。

Double DQN为了减缓Q值高估的问题。计算目标Q值时，无论是Naive DQN的$\underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })$，还是Double DQN的$\underset{a^{\prime }}{\max }{Q}_{target}(s^{\prime },a^{\prime })$由于max操作直接作用在$Q_{target}$上，会使目标Q值被过估计。为此，Double DQN将Nature DQN的目标Q值修改为：
$$target\_q=r+\gamma \ast (1-mask)\ast Q_{target}(s^{\prime },\underset{a^{\prime }}{\mathrm{argmax}}Q(s^{\prime },a^{\prime }))$$很显然，相比于Nature DQN，$Q_{target}(s^{\prime },\underset{a^{\prime }}{\mathrm{argmax}}Q(s^{\prime },a^{\prime }))\le \underset{a^{\prime }}{\max }{Q}_{target}(s^{\prime },a^{\prime })$，故Double DQN能减缓目标Q值的过估计。

Dueling DQN
不同于Double DQN修改目标Q值的计算来优化DQN算法，Dueling DQN通过优化神经网络的结构来优化算法。优势函数定义为：$$A^{\ast }(s,a)=Q^{\ast }(s,a)-V^{\ast }(s)$$$V^{\ast }(s)$视作baseline，则$A^{\ast }(s,a)$就是$Q^{\ast }(s,a)$相对基线的优势。通过变换，Q值为$$Q^{\ast }(s,a)=V^{\ast }(s)+A^{\ast }(s,a)$$，为了解决不唯一性，使用如下的等价修改$$Q^{\ast }(s,a)=V^{\ast }(s)+A^{\ast }(s,a)-\underset{maxa}{A^{\ast }}(s,a)$$因为$\underset{maxa}{A^{\ast }}(s,a)=\underset{maxa}{Q^{\ast }}(s,a)-V^{\ast }(s)==V^{\ast }(s)-V^{\ast }(s)=0$，实际应用中使用mean代替max，即$$Q^{\ast }(s,a)=V^{\ast }(s)+A^{\ast }(s,a)-\underset{meana}{A^{\ast }}(s,a)$$

此外，还有一些用于解决奖励稀疏问题的通用trick，例如优先经验回放 (Prioritized Experience Replay, PER)、事后经验回放 (Hindsight Experience Replay, HER) 等，由于它们独立于算法之外，是通用trick，而不属于某个具体算法例如DQN，故与普遍的做法不同，这里不将Prioritized Replay DQN视为DQN的一个算法版本。

4.3 策略梯度算法

value-based与policy-based

上述的DQN及其变体都属于value-based算法，它们不直接拟合策略，而是拟合（估计）Q值，由Q值来间接地得到策略，例如$greedy$或$ϵ-greedy$方法。

DQN这类value-based算法一般只能处理离散动作，无法处理连续动作（虽然可以连续动作离散化），因为由Q值(间接)得到动作时，需要对状态s对应的所有动作的Q值进行比较，选取Q值最大的动作，即$\underset{a}{\mathrm{argmax}}Q(s,a)$，当动作连续或者有很高的维度时，max操作将没法进行。

当然value-based方法还有一些其他的缺陷，像不能很好地处理多模态的最优动作，例如最优策略是随机策略。

而另一类policy-based的策略梯度方法直接拟合策略，以状态或观测作为输入，输出各个动作的概率${\pi }_{\theta }(s,a)$ ( Stochastic Policy Gradient, SPG)或输出最优动作$u_{\theta }(s)$ (Deterministic Policy Gradient, DPG)。
显然，DPG可以解决连续型动作，因为其不依赖动作的维度。

4.4 Actor-Critic架构

value-based和policy-based相结合的AC结构在model free RL中相当流行，很多经典高效的算法采用AC结构，例如DDPG及其改进版TD3、SAC等。

在AC结构中，Actor网络负责由状态选择动作，Critic负责对Actor的决策进行评价。Actor网络的更新采用policy-based方式，即梯度上升，只不过其Q(s,a)由Critic网络输出；Critic一般使用类似DQN中的TD-error更新。
注意，为了能够处理连续型动作，Critic网络的输入得是cat(s,a)，而不能像DQN那样，可以仅输入s，而输出各个动作对应的Q值。