常见的几种normalization方法

这篇笔记主要来自余庭嵩的讲解。

几种常见的normalization方法

基本知识

为什么要normalization？因为如果初始值分布不好时，数据尺度会随着网络层数加深而变化异常，详情可参考之前这篇笔记：梯度消失或梯度爆炸原理。而normalization不仅可以解决这样的问题，还可以给神经网络训练的过程带来更多其他方便，所以就出现了不同的normalization方法。几种常见的normalization方法有：batch normalization，layer normalization，instance normalization以及group normalization等等。建议先看BN部分的内容之后再看其他部分。

数学原理

如果一批数据（数据集）含有m个样本输入$x_1,x_2,\dots ,x_m$。
这批数据的均值为
$${\mu }_{\mathcal{B}}\leftarrow \frac{1}{m}\sum _{i=1}^m{x}_i$$
这批数据的方差为
$${\sigma }_{\mathcal{B}}^2\leftarrow \frac{1}{m}\sum _{i=1}^m{\left(x_i-{\mu }_{\mathcal{B}}\right)}^2$$
那么如何将这一批数据的方差转变成1，也就是如何标准化？对每个$x_i$进行如下操作（下面的$ϵ$是防止分母是0）
$$x_i\leftarrow \frac{x_i-{\mu }_{\mathcal{B}}}{\sqrt{{\sigma }_{\mathcal{B}}^2+ϵ}}$$
那如何将这一批数据的均值变为0？或者如何对数据进行平移和缩放？
$$y_i\leftarrow \gamma x_i+\beta \equiv \mathrm{B}{\mathrm{N}}_{\gamma ,\beta }\left(x_i\right)$$
这一步骤就叫affine transform。这里的两个参数$\gamma$，$\beta$是可学习的参数，让模型自己选择是否对数据进行变换操作。这里还有一个重要的点，如果$\gamma$，$\beta$分别学习为是方差和均值，那么标准化操作将被逆操作回来，由此就可视为没有标准化这一步。这就使得模型更加灵活了。
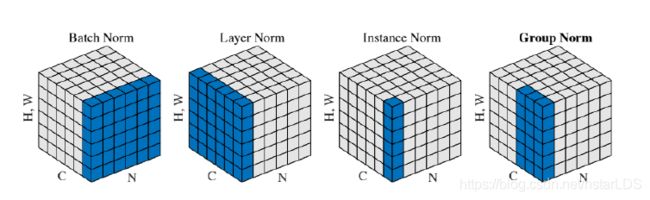
这里的BN，LN，IN和GN相同的地方是：对于每一个样本的操作都是一样的，都是按照上面最后两个公式进行操作
不同的地方是：上面开头两个公式，也就是均值和方差的求取方式不一样。BN是在batch中寻找均值和方差，LN是在网络层里面寻找均值和方差，IN是依据实例求取均值方差（图像生成），GN是分组求取均值和方差。

Batch Normalization (BN)

由于batch normalization篇幅较大，实验较多，所以单写了一篇笔记：动手理解Batch Normalization，里面对batch normalization从理论到实验都进行了探讨说明。

Layer Normalization (LN)

LN主要出自文章《Layer Normalization》，如果想知道更多细节和实验对比，可以看原文。
起因：BN不适用于变长的网络，如RNN
思路：逐层计算均值和方差，每个网络层的输出都有其均值方差。

注意事项：
不再有running_mean和running_var，因为给定特征图的情况下都是固定的标量了，是根据该层内所有元素的均值和方差计算的。
两个参数$\gamma$和$\beta$是逐元素的，也就是每个神经元都有其参数$\gamma$和$\beta$。

pytorch中的LN

主要参数有

• normalized_shape：该层的特征形状
• eps：分母修正项，默认1e-5
• elementwise_affine：是否需要affine transform，默认true

代码实例如下，需要给nn.LayerNorm传递的参数是特征的shape（除去batch维），需要从后往前设置维度，例如数据是AxBxCxD的，可以输入D，[C, D]，但是不可以输入[B, C]：

batch_size = 8
num_features = 6

features_shape = (3, 4)

feature_map = torch.ones(features_shape)
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)
feature_maps_bs = torch.stack([feature_maps for i in range(batch_size)], dim=0)

ln = nn.LayerNorm(feature_maps_bs.size()[1:], elementwise_affine=True)

output = ln(feature_maps_bs)

print("Layer Normalization")
print(ln.weight.shape)
print(feature_maps_bs[0, ...])
print(output[0, ...])

输出结果：

Layer Normalization
torch.Size([6, 3, 4])
tensor([[[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[2., 2., 2., 2.],
         [2., 2., 2., 2.],
         [2., 2., 2., 2.]],

        [[3., 3., 3., 3.],
         [3., 3., 3., 3.],
         [3., 3., 3., 3.]],

        [[4., 4., 4., 4.],
         [4., 4., 4., 4.],
         [4., 4., 4., 4.]],

        [[5., 5., 5., 5.],
         [5., 5., 5., 5.],
         [5., 5., 5., 5.]],

        [[6., 6., 6., 6.],
         [6., 6., 6., 6.],
         [6., 6., 6., 6.]]])
tensor([[[-1.4638, -1.4638, -1.4638, -1.4638],
         [-1.4638, -1.4638, -1.4638, -1.4638],
         [-1.4638, -1.4638, -1.4638, -1.4638]],

        [[-0.8783, -0.8783, -0.8783, -0.8783],
         [-0.8783, -0.8783, -0.8783, -0.8783],
         [-0.8783, -0.8783, -0.8783, -0.8783]],

        [[-0.2928, -0.2928, -0.2928, -0.2928],
         [-0.2928, -0.2928, -0.2928, -0.2928],
         [-0.2928, -0.2928, -0.2928, -0.2928]],

        [[ 0.2928,  0.2928,  0.2928,  0.2928],
         [ 0.2928,  0.2928,  0.2928,  0.2928],
         [ 0.2928,  0.2928,  0.2928,  0.2928]],

        [[ 0.8783,  0.8783,  0.8783,  0.8783],
         [ 0.8783,  0.8783,  0.8783,  0.8783],
         [ 0.8783,  0.8783,  0.8783,  0.8783]],

        [[ 1.4638,  1.4638,  1.4638,  1.4638],
         [ 1.4638,  1.4638,  1.4638,  1.4638],
         [ 1.4638,  1.4638,  1.4638,  1.4638]]], grad_fn=)

Instance Normalization (IN)

起因：BN在图像生成中不适用，每个batch中的图像有不同的风格，模式和style，所以不能把一个batch中的数据拿到一起计算。
思路：逐instance（channel）计算均值和方差
例如，AxBxCxD的图，A是batchsize，B是channel数，C和D代表一张图的所有像素点。那么是不可以使用nn.batchnorm2d那样直接把各个batch的对应相同通道的特征图拿在一起计算均值和方差的。
所以instance normalization就是不仅逐样本，还逐通道地计算每一个特征图（CxD）的均值和方差。

Group Normalization (GN)

可参考论文《Group Normalization》
起因：在小batch样本中，BN估计不准确。样本越多，估计的均值和方差就比较准，但如果batchsize是1或者2的时候，估计的样本就很少，这样估计值就不准确。那么这个情况下再计算所有batch在该特征下的平均值和方差就不可行了，就需要把多个特征合并一下，并为一组（group），来求均值和方差。
注意：和layernorm一样，不再有running_mean和running_var，两个参数$\gamma$和$\beta$是逐通道的。
应用场景：大模型，特征数非常多，此时的batchsize只能设置比较小。

PyTorch中的使用

主要参数：
num_groups：分组数，一般是2的n次幂，因为其要能被特征数整除
num_channels：通道数

代码实例

batch_size = 2
num_features = 4
num_groups = 2

features_shape = (2, 2)

feature_map = torch.ones(features_shape)    # 2D
feature_maps = torch.stack([feature_map * (i + 1) for i in range(num_features)], dim=0)
feature_maps_bs = torch.stack([feature_maps * (i + 1) for i in range(batch_size)], dim=0)  # 4D

gn = nn.GroupNorm(num_groups, num_features)
outputs = gn(feature_maps_bs)

print("Group Normalization")
print(gn.weight.shape)
print(outputs[0])

输出结果为

Group Normalization
torch.Size([4])
tensor([[[-1.0000, -1.0000],
         [-1.0000, -1.0000]],

        [[ 1.0000,  1.0000],
         [ 1.0000,  1.0000]],

        [[-1.0000, -1.0000],
         [-1.0000, -1.0000]],

        [[ 1.0000,  1.0000],
         [ 1.0000,  1.0000]]], grad_fn=)

总结