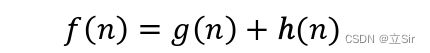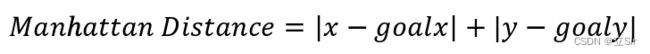【路径规划】(2) A* 算法求解最短路，附python完整代码

大家好，今天和各位分享一下机器人路径规划中非常经典的 A* 算法，感兴趣的点个关注，文末有 python 代码，那我么开始吧。

---

1. 算法介绍

A* 算法是 1968 年 P.E.Hart[1]等人所提出的在全局地图环境中所有已知情形下求解最短路径问题的方法，由于其简洁高效，容易实施等优点而受到人们的广泛关注。但是，A*算法在实际应用过程中也暴露出其严重弊端，例如：在搜索空间较大的环境下，增加了算法的执行时间，从而大大降低了路线规划效果；复杂环境下，由于地图精度不高，从而减小了获取最佳路径的可能性；在搜索过程中存在相同 F 值无法得到最佳路线等问题。

而面对上述问题，不同的研发人员也以不同的方法以对其做出了改善，并获得了不少研究成果。

Korf 等人[2]在 A*算法的基础上构建了迭代改进的 IDA* 算法，在计算过程中根据迭代次数得到最优解，解决了A*算法容易陷入盲目搜索的不足；Tran HAM[3]等人在 A*算法基础上构建了一种基于视觉的路径规划和导航算法，然后对搜索的路径进行优化。Szczerba[4]等人提出了稀疏 A*算法，在传统 A*算法基础上添加相应的约束条件，根据不同的约束条件修改 A*算法的搜索空间，提升了路线规划效果，大大增加了获取最佳路径的可能性。

参考文献：

[1] Hart P E, Nilsson N J, Raphael B. A formal basis for the heuristic determination of minimum cost paths[J]. IEEE transactions on Systems Science and Cybernetics, 1968, 4(2): 100-107. 

[2] Korf,  Richard  E.  Depth-first  iterative-deepening:  an  optimal  admissible  tree  search[J]. Artificial Intelligence, 1985, 27(1):97-109. 

[3] Tran H  A M, Ngo H Q  T,  Nguyen  T  P,  et  al.  Implementation  of  vision-based  autonomous mobile platform to control by A* algorithm[C]//2018 2nd International Conference on Recent Advances in Signal Processing, Telecommunications & omputing (SigTelCom). IEEE, 2018: 39-44.  

[4] Szczerba R J, Galkowski P, Glicktein I S, et al. Robust algorithm for real-time route planning[J]. IEEE Transactions on Aerospace & Electronic Systems, 2000, 36(3):869-878.   

---

2. 算法原理

经典 A* 算法主要用在静态且周围环境已知的情况下，是建立在 Dijkstra 和BFS 基础上的启发式遍历搜索算法，在路径规划时不仅要考虑自身与最近节点位置的距离（Dijkstra 实现），还需要考虑自身位置与目标点的距离（BFS 实现）。与传统的遍历搜索算法相比，弥补了搜索过程中的贪心机制，从而很好地完成路径规划的任务。

2.1 基本原理

A* 算法以起点为中心开始进行路径规划，并在路径规划过程中扩展周围的邻近节点。通过 A*算法公式对起始点到当前位置和当前位置到目标点的代价值进行计算。在所有的节点中选取代价值最小的节点作为当前最优节点，以当前最优节点继续搜索，直到搜索到目标点，最后生成一条从起始点到目标点的路径。

A* 算法本身遵循 821 定律，同时在搜索过程中将节点的状态定义为未检查、待检查、已检查三种准备状态；8 是指以当前定位点周围的 8 个邻域的代价值作为计算目标，2 是指两个参数列表，一个是 open list 列表，存放待检查的节点；另外一个是 close list 列表，存放已检查完成不再需要关注的节点，1 是指一个计算公式，如下。 

其中，f(n) 是指当前节点 n 的全局代价值，g(n) 是指从起始点到当前节点 n 的实际代价值，h(n) 是指当前节点 n 到终点的预测值。

---

2.2 案例解析

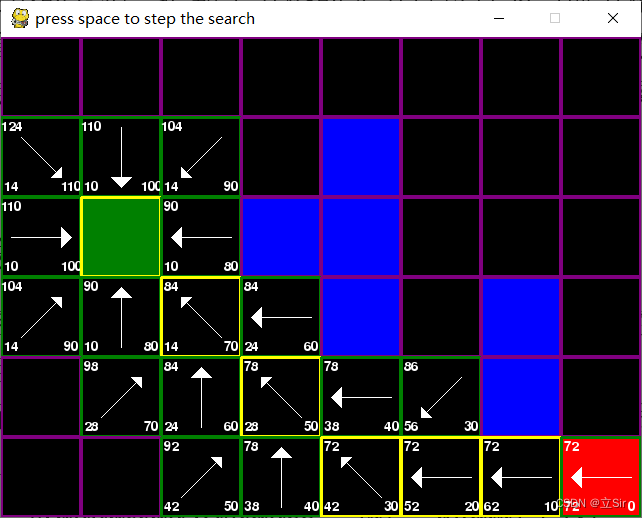
A* 算法整体搜索过程如下图所示，图中绿色格子为寻径起始点，红色格子为寻径终止点，蓝色代表障碍物。从起始点开始，将其放到 open list 列表中，同时让其作为当前节点。通过当前节点查找与其相邻的 8 个邻域节点，如图中带有绿色线条的方格。8 个邻域节点方格中，箭头指向的方向为当前相邻节点 n 的父节点，用于代价值的计算以及最终路径的回溯。 

以起始点作为当前节点，通过 A* 算法代价公式计算相邻节点的 f 值，并将起始节点放入 close list 列表中。起始点周围每个方格节点的三个夹角处由数字标识，其中左下角表示的是从起始点到当前节点 n 的真实代价值 g(n)，如果起始点到当前节点 n 是在横向上往前/后移动了一个节点，或者在竖直方向上往上/下移动了一个节点，普遍设定 g(n) 移动一个节点的代价为 10；如果起始点到当前节点 n 是经过对角方向的移动，普遍设定 g(n) 的移动代价值为 14。右下角表示的是从当前节点 n 到终点的预估值 h(n)，通过启发函数进行计算。左上角表示的是全局代价值 f(n)，将以上计算出的 g(n)与 h(n)相加可得到对应的 f(n)。 

基于以上计算，进一步判断当前节点的 8 个邻域节点是否在 open list 列表中，如果某个邻域节点未在 open list 列表中，则将带有 f  值的邻节点添加到 open list 列表中；如果某个邻域节点已经存放在 open  list 表中，则以当前方格为父节点检查经由当前父节点到达那个方格是否具有更小的 g 值，如果没有不做任何操作，如果存在更小的 g 值，把那个方格的父节点设置为当前方格，然后重新计算那个方格的 g 值和 f 值。判断完成之后，获取 open list 列表中最小代价值节点。从上图中可以看出起始点周围相邻节点的全局代价值 f 根据从上到下、从左向右的顺序分别为 124、110、104、110、90、104、90、84，从以上数字中选取 f 值最小的 84 的点作为当前节点。 

循环上述搜索步骤，直至搜索到右侧的红色目标点，将目标点添加到 close list 列表中。根据close list 列表中的各个节点按照父节点的指向逆序输出，从而得到搜索路径。如下图所示，带有黄色边框的格子节点为最终搜索到的最佳路径。 

---

2.3 启发函数

在路径规划时，通常需要寻找一些与搜索环境相关的特征信息，在计算过程中，将这些特征信息称为启发函数。启发函数被用来估计从当前节点到目标节点生成的代价值。常用的启发函数主要包括曼哈顿距离函数、欧氏距离函数、对角距离函数三种。 

假设起点的坐标为 (, )，终点的坐标为 (, )，对三种启发函数进行分析。 

（1）曼哈顿距离函数。曼哈顿距离为起点与终点坐标点绝对值总和，公式如下：

（2）欧式距离函数。 欧式距离为搜索环境中起止两节点间的最短直线距离，公式如下：

（3）对角距离函数。 对角距离首先允许沿对角线运动，然后通过水平和垂直运动完成剩下路线，
或者相反。公式如下： 

沿对角线运动的公式：

 沿水平和垂直运动的公式：

将对角线、水平和垂直运动组合构成的对角距离公式：

---

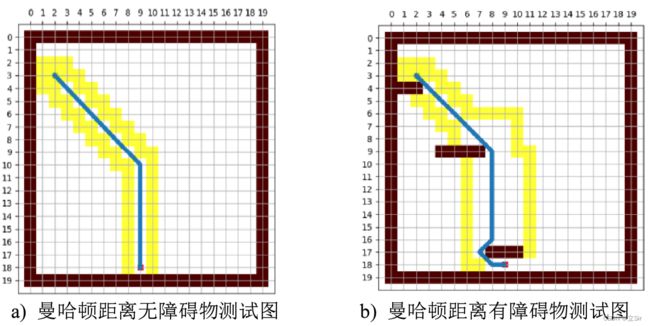
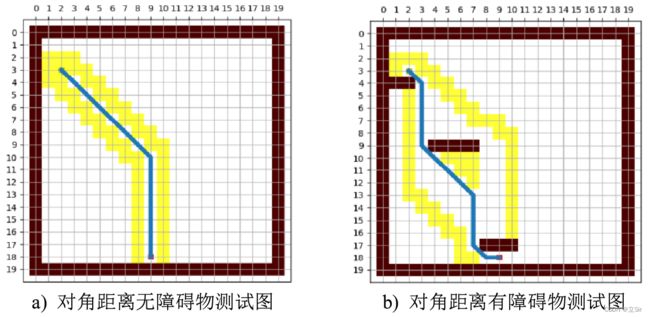
下面对三种启发函数做实验，其中图中黄色方格节点为寻径起始点，红色方格节点为寻径终点。空白区域为可行走安全区，深红色连续方格节点为不可通行障碍物区域。

图中蓝色曲线为从起始点到目标点搜索的路径，而路径周围黄色的方格节点代表在路径搜索过程中添加到 open list 列表的节点。根据上述三种路径搜索对比可知，在无障碍物情况下曼哈顿距离和对角距离运行情况相对较好，而欧式距离搜索出的路径不够平滑；在存在障碍物情况下曼哈顿距离搜索路径较平滑，欧式距离和对角距离在搜索过程中产生了大量的搜索节点，搜索路径出现较多的转折点，运行时间较长。 

综上所知，在 A*算法中选择曼哈顿启发函数不仅能减少搜索节点数，还能能到相对平滑路径。

---

3. 代码实现

3.1 算法基本步骤

（1）设置 open list 列表和 close list 列表，将起始点存放 open list 列表中，此时 close list 列表为空；

（2）取出 open list 列表中 f 值最小的节点 P 作为当前节点，并进行以下操作：判断当前节点 P 是否为目标点 end，如果点 P 为目标点寻径结束，将目标点end 的父节点设置为节点 P，然后返回由目标节点逆序倒推其父节点至起始点的所有节点组成的路径。如果不是目标点，将当前节点 P 加入到 close list 列表中并从 open list 列表删除，执行步骤（3）； 

（3）算法遍历当前节点 P 的相邻节点 P'，并进行以下操作； 

（4）如果相邻节点 p' 不在 open list 列表中，计算 g、h 值，设置相邻节点 P' 的父节点设置为节点 P，最后将节点 P' 存放到 open list 列表中； 

（5）如果相邻节点 P' 是不可行区域或在 close list 列表中，则不做任何处理；

（6）如果相邻节点 P' 已在 open list 列表中，计算经由当前节点 P 到达邻节点 P' 的 g 值是否比邻节点 P' 此时的 g 值更小，如果更小，则将相邻节点 P' 的 g 值更新为从当前节点 P 到相邻节点 P' 的 g 值，并将相邻节点 P' 的父节点设置为节点P；如果不会更小，则不做任何处理； 

（7）返回步骤（3），继续处理余下的相邻节点； 

（8）判断 open list 列表是否为空，如果为空，搜索结束，未找到有效路径；若非空，执行步骤（2）。 

重复执行以上八步，直至找到目标点。

---

3.2 代码展示

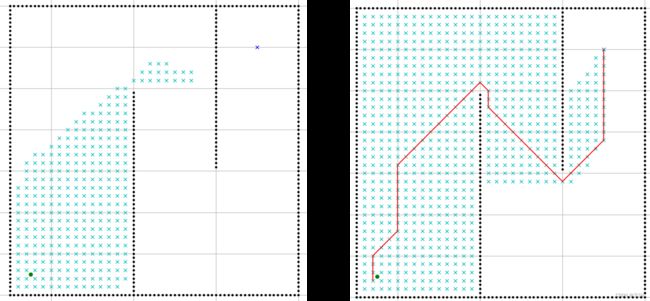
左图为节点搜索过程，右图为最优路径

完整代码如下，注释很全，有问题在评论区留言

import math
import matplotlib.pyplot as plt
min_set = 10
show_animation = True  # 绘图

# 创建一个类
class Dijkstra:
    # 初始化
    def __init__(self, ox, oy, resolution, robot_radius):
        # 属性分配
        self.min_x = None
        self.min_y = None
        self.max_x = None
        self.max_y = None
        self.x_width = None
        self.y_width = None
        self.obstacle_map = None
        
        self.resolution = resolution  # 网格大小(m)
        self.robot_radius = robot_radius  # 
        self.calc_obstacle_map(ox, oy)  # 绘制栅格地图
        self.motion = self.get_motion_model()  # 机器人运动方式

    # 构建节点，每个网格代表一个节点
    class Node:
        def __init__(self, x, y, cost, parent_index):
            self.x = x  # 网格索引
            self.y = y
            self.cost = cost  # 路径值
            self.parent_index = parent_index  # 该网格的父节点
        def __str__(self):
            return str(self.x) + ',' + str(self.y) + ',' + str(self.cost) + ',' + str(self.parent_index)

    # 寻找最优路径，网格起始坐标(sx,sy)，终点坐标（gx,gy）
    def planning(self, sx, sy, gx, gy):
        # 节点初始化
        # 将已知的起点和终点坐标形式转化为节点类型，0代表路径权重，-1代表无父节点
        start_node = self.Node(self.calc_xy_index(sx, self.min_x),
                               self.calc_xy_index(sy, self.min_y), 0.0, -1)
        # 终点
        goal_node = self.Node(self.calc_xy_index(gx, self.min_x),
                              self.calc_xy_index(gy, self.min_y), 0.0, -1)
        # 保存入库节点和待计算节点
        open_set, closed_set = dict(), dict()
        # 先将起点入库，获取每个网格对应的key
        open_set[self.calc_index(start_node)] = start_node

        # 循环
        while 1:
            # 选择扩展点，添加了启发项，f(n)= g(n) + h(n)
            c_id = min(open_set, 
                       key=lambda o: open_set[o].cost + \
                           self.calc_heuristic(goal_node, open_set[o]))

            current = open_set[c_id]  # 从字典中取出该节点

            # 绘图
            if show_animation:
                # 网格索引转换为真实坐标
                plt.plot(self.calc_position(current.x, self.min_x),
                         self.calc_position(current.y, self.min_y), 'xc')
                plt.pause(0.0001)
            
            # 判断是否是终点，如果选出来的损失最小的点是终点
            if current.x == goal_node.x and current.y == goal_node.y:
                # 更新终点的父节点
                goal_node.cost = current.cost
                # 更新终点的损失
                goal_node.parent_index = current.parent_index
                break
            
            # 在外库中删除该最小损失点，把它入库
            del open_set[c_id]
            closed_set[c_id] = current

            # 遍历邻接节点
            for move_x, move_y, move_cost in self.motion:
                # 获取每个邻接节点的节点坐标，到起点的距离，父节点
                node = self.Node(current.x + move_x,
                                 current.y + move_y, 
                                 current.cost + move_cost, c_id)
                # 获取该邻居节点的key
                n_id = self.calc_index(node)

                # 如果该节点入库了，就看下一个
                if n_id in closed_set:
                    continue
                
                # 邻居节点是否超出范围了，是否在障碍物上
                if not self.verify_node(node):
                    continue

                # 如果该节点不在外库中，就作为一个新节点加入到外库
                if n_id not in open_set:
                    open_set[n_id] = node
                # 节点在外库中时
                else:
                    # 如果该点到起点的距离，要小于外库中该点的距离，就更新外库中的该点信息，更改路径
                    if node.cost <= open_set[n_id].cost:
                        open_set[n_id] = node
            
        # 找到终点
        rx, ry = self.calc_final_path(goal_node, closed_set)
        return rx, ry

    # ------------------------------ #
    # A* 的启发函数
    # ------------------------------ #
    @staticmethod
    def calc_heuristic(n1, n2):  # n1终点，n2当前网格
        w = 1.0  # 单个启发函数的权重，如果有多个启发函数，权重可以设置的不一样
        d = w * math.hypot(n1.x-n2.x, n1.y-n2.y)  # 当前网格和终点距离
        return d

    # 机器人行走的方式，每次能向周围移动8个网格移动
    @staticmethod
    def get_motion_model():
        # [dx, dy, cost]
        motion = [[1,0,1],  # 右
                  [0,1,1],  # 上
                  [-1,0,1], # 左
                  [0,-1,1], # 下
                  [-1,-1,math.sqrt(2)], # 左下
                  [-1,1,math.sqrt(2)], # 左上
                  [1,-1,math.sqrt(2)], # 右下
                  [1,1,math.sqrt(2)]]  # 右上
        return motion

    # 绘制栅格地图
    def calc_obstacle_map(self, ox, oy):
        # 地图边界坐标
        self.min_x = round(min(ox))  # 四舍五入取整
        self.min_y = round(min(oy)) 
        self.max_x = round(max(ox))
        self.max_y = round(max(oy))
        # 地图的x和y方向的栅格个数，长度/每个网格的长度=网格个数
        self.x_width = round((self.max_x-self.min_x)/self.resolution)  # x方向网格个数
        self.y_width = round((self.max_y-self.min_y)/self.resolution)  # y方向网格个数
        # 初始化地图，二维列表，每个网格的值为False
        self.obstacle_map = [[False for _ in range(self.y_width)]
                             for _ in range(self.x_width)]
        # 设置障碍物
        for ix in range(self.x_width):  # 遍历x方向的网格 [0:x_width]
            x = self.calc_position(ix, self.min_x)   # 根据网格索引计算x坐标位置
            for iy in range(self.y_width):  # 遍历y方向的网格 [0:y_width]
                y = self.calc_position(iy, self.min_y)  # 根据网格索引计算y坐标位置
                # 遍历障碍物坐标(实际坐标)
                for iox, ioy in zip(ox, oy):
                    # 计算障碍物和网格点之间的距离
                    d = math.hypot(iox-x, ioy-y)
                    # 膨胀障碍物，如果障碍物和网格之间的距离小，机器人无法通行，对障碍物膨胀
                    if d <= self.robot_radius:
                        # 将障碍物所在网格设置为True
                        self.obstacle_map[ix][iy] = True
                        break  # 每个障碍物膨胀一次就足够了

    # 根据网格编号计算实际坐标
    def calc_position(self, index, minp):
        # minp代表起点坐标，左下x或左下y
        pos = minp + index * self.resolution  # 网格点左下左下坐标
        return pos

    # 位置坐标转为网格坐标
    def calc_xy_index(self, position, minp):
        # (目标位置坐标-起点坐标)/一个网格的长度==>目标位置的网格索引
        return round((position-minp) / self.resolution)

    # 给每个网格编号，得到每个网格的key
    def calc_index(self, node):
        # 从左到右增大，从下到上增大
        return node.y * self.x_width + node.x

    # 邻居节点是否超出范围
    def verify_node(self, node):
        # 根据网格坐标计算实际坐标
        px = self.calc_position(node.x, self.min_x)
        py = self.calc_position(node.y, self.min_y)
        # 判断是否超出边界
        if px < self.min_x:
            return False
        if py < self.min_y:
            return False
        if px >= self.max_x:
            return False
        if py >= self.max_y:
            return False
        # 节点是否在障碍物上，障碍物标记为True
        if self.obstacle_map[node.x][node.y]:
            return False
        # 没超过就返回True
        return True


    # 计算路径, parent属性记录每个节点的父节点
    def calc_final_path(self, goal_node, closed_set):
        # 先存放终点坐标（真实坐标）
        rx = [self.calc_position(goal_node.x, self.min_x)]
        ry = [self.calc_position(goal_node.y, self.min_y)]
        # 获取终点的父节点索引
        parent_index = goal_node.parent_index
        # 起点的父节点==-1 
        while parent_index != -1:
            n = closed_set[parent_index]  # 在入库中选择父节点
            rx.append(self.calc_position(n.x, self.min_x))  # 节点的x坐标
            ry.append(self.calc_position(n.y, self.min_y))  # 节点的y坐标
            parent_index = n.parent_index  # 节点的父节点索引

        return rx, ry


def main():
    # 设置起点和终点
    sx = -5.0
    sy = -5.0
    gx = 50.0
    gy = 50.0
    # 网格大小
    grid_size = 2.0
    # 机器人半径
    robot_radius = 1.0 

    # 设置障碍物位置
    ox, oy = [], []
    for i in range(-10,60):    ox.append(i); oy.append(-10.0)  # 下边界
    for i in range(-10,60):    ox.append(60.0); oy.append(i)  # 右边界
    for i in range(-10,61):    ox.append(i); oy.append(60.0)  # 上边界
    for i in range(-10,61):    ox.append(-10.0); oy.append(i)  # 左边界
    for i in range(-10,40):    ox.append(20.0); oy.append(i)  # 左围栏
    for i in range(0,40):      ox.append(40.0); oy.append(60-i)  # 右围栏

    # 绘图
    if show_animation:
        plt.plot(ox, oy, '.k')  # 障碍物黑色
        plt.plot(sx, sy, 'og')  # 起点绿色
        plt.plot(gx, gy, 'xb')  # 终点蓝色
        plt.grid(True)
        plt.axis('equal')  # 坐标轴刻度间距等长

    # 实例化，传入障碍物，网格大小
    dijkstra = Dijkstra(ox, oy, grid_size, robot_radius)
    # 求解路径，返回路径的 x 坐标和 y 坐标列表
    rx, ry = dijkstra.planning(sx, sy, gx, gy)

    # 绘制路径经过的网格
    if show_animation:
        plt.plot(rx, ry, '-r')
        plt.pause(0.01)
        plt.show()

if __name__ == '__main__':
    main()