【复习笔记】画法几何与土木水利工程制图知识点总结
我是灼灼,一只初学Java的大一金渐层。
向往余秀华和狄兰·托马斯的疯狂,时常沉溺于将情感以诗相寄;追逐过王尔德、王小波的文字,后陷于毛姆和斯蒂芬·金不可自拔;热爱文学的浪潮,白日梦到底却总在现实里清醒;艳羡平静又极度渴盼奔跑的力量。
欢迎与我交流鸭· QQ:1517526827;
个人博客:https://blog.csdn.net/weixin_52777510?spm=1001.2101.3001.5343
画法几何与土木水利工程制图
开学考试,考前挣扎一下~
【大一第一学期】
考察范围:第3章到第10章全部内容
考点整合+知识点总结
知识概览如下:
文章目录
- 画法几何与土木水利工程制图
-
- 第3章|投影基本知识点及点的投影
-
- 3.3点的投影
-
- 3.3.1 点在两面投影体系中的投影
-
- 1.两面投影体系
- 2.点的两面投影体系及其作用规律
- 3.3.2 点在三面投影体系中的投影
-
- 1.三面投影体系
- 2.点的三面投影及其作图规律
- 3.点的投影与直角坐标的关系
- 4.特殊位置点的投影
- 3.3.3 点的相对位置
- 3.3.4 其它分角点的投影
- 第4章|直线的投影
-
- 4.1直线的投影及分析
-
- 4.1.1 直线的投影表示
- 4.1.2 各种位置直线及投影特性
-
- 1.一般位置直线
- 2.投影面平行线
- 3.投影面垂直线
- 4.1.3 一般位置直线的实长及倾角
- 4.2|直线上的点
-
- 4.2.1 直线上点的投影特性
- 4.2.2 直线的迹点
第3章|投影基本知识点及点的投影
3.3点的投影
空间形体的表面可看作由点、线、面的集合组成。
3.3.1 点在两面投影体系中的投影
1.两面投影体系
局限:单面投影不能准确地表达空间形体的形状及位置。
- 两个相互垂直的投影面,正投影面V,与正投影面垂直的水平面为H;二者构成的投影体系称为两面投影体系。
- V面与H面的交线称为OX投影轴。
2.点的两面投影体系及其作用规律
- 空间点A在H面得到的投影用小写字母a表示,在V面得到的投影用a’表示。
- 两面投影可唯一确定一个空间点。
为了使两个投影能画在一张二维平面的图纸上,国标规定:V面保持不动,H面向下旋转90度,与V面处于同一平面。这时去除对应的空间点,即在平面上形成了点的两面投影。为了方便画图,可将投影平面的边框去掉。
点的两面投影作图规律:
- 点的两面投影连线垂直于它们之间的投影轴。
- 点的H面投影到OX轴的距离等于点到V面的距离,点的V面投影到OX轴的距离等于点到H面的距离。
3.3.2 点在三面投影体系中的投影
1.三面投影体系
在两面投影体系中,再增加一个与V面和H面都垂直的侧投影面,用W表示。此时W面分别于V面、H面产生两条交线,其中与V面交线称为OZ轴,与H面交线称为OY轴,原来两面投影体系中OX轴保持不变,三条轴交于点O,这样就形成了三面投影体系。
2.点的三面投影及其作图规律
空间点A在V、H两面投影的基础上再向W面作正投影,得到点的W面投影a’’,形成点的三面投影。
为了使三个投影能画在一张平面图纸上,V面保持不变,将H面向下、W面向后旋转90度,H面、W面即与V面处于同一平面,得到点的投影展开图。其中随H面旋转后的OY轴标记为OYH,随W面旋转后的OY轴标记为OYw。
点的V面投影a’与点的H面投影a,以及点的V面投影a’与点的W面投影a’‘都符合两面投影体系作图规律,而点的H面投影a到OX轴的距离以及点的W面投影a’'到OZ轴的距离都能反映点A到V面的距离。
点的三面投影作图规律:
- 点的V面投影与H面投影的连线垂直于OX轴。【长对正】
- 点的V面投影与W面投影的连线垂直于OZ轴。【高平齐】
- 点的H面投影到OX轴的距离等于点的W面投影到OZ轴的距离。【宽相等】
3.点的投影与直角坐标的关系
三个相互垂直的投影轴构成一个空间直角坐标系,空间点A的位置可用坐标值A(x,y,z)表示。
4.特殊位置点的投影
- 投影面上的点。点处于投影面上时,点在该投影面(X轴对应W面,Y轴对应V面,Z轴对应H面)上的投影与空间点本身重合,其余两投影在相应的投影轴(除去该投影面对应的投影轴后)上。【投影名要写在对应的投影面上】
- 投影轴上的点。点处于投影轴上时,其两面投影都与空间点本身重合,第三投影(为投影轴所对应面的投影)落在O点。
3.3.3 点的相对位置
空间两点的相对位置是指空间两点的上下、左右、前后位置关系,可以用它们的绝对坐标之差达尔特X、达尔特Y、达尔特Z来表示。
如果已知点A的三面投影,又知点B与点A的相对位置,即使不画投影轴,也可以确定点B的三面投影。这就形成了
,此时并不关心点到投影面的距离,而只关心它们的相对位置保持不变。
当空间两点位于同一投射线上时,它们在投影面上的投影重合,称为该投影面的重影点(通常在两面投影体系中)——
-
三面投影体系中只有一个坐标不同。
-
重影点可见性的判断:
除重影的投影面外的其它投影面上,坐标值大的点可见。
即上、左、前可见。
3.3.4 其它分角点的投影
我们一般只研究第一分角。
第一分角(四个分角可以看作是数学中的四个象限,一一对应)
第4章|直线的投影
4.1直线的投影及分析
4.1.1 直线的投影表示
直线在空间的位置可由直线上的任意两点确定。要作直线的各个投影,一般只需作出该直线上任意两点(通常取线段的两个端点)在各个投影面上的投影,然后分别用粗实线连接两点在同一投影面上的投影(同面投影),即可得到直线的投影图。
已知属于直线的一点的投影和该直线方向的投影,也可画出该直线的投影。
4.1.2 各种位置直线及投影特性
在三面投影体系中,按直线与H、V、W面的相对位置,分为一般位置直线、投影面平行线和投影面垂直线三大类。
1.一般位置直线
与三个基本投影面既不平行也不垂直的直线称为一般位置直线。
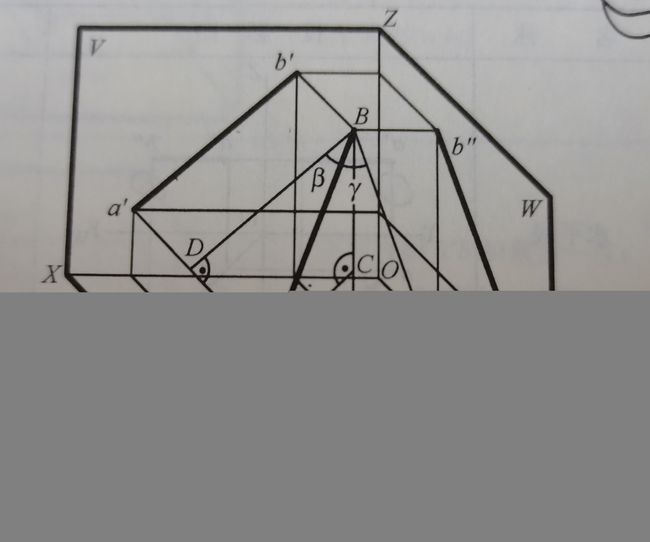
直线与其在某投影面上的投影之间所夹锐角记作直线对该投影面的倾角,在此规定直线与H、V及W三投影面的夹角分别用阿尔法、贝塔、伽马来表示。{一般位置直线的这三个倾角既不等于0度,也不等于90度}
因直线倾斜于各投影面,所以各点坐标不同。
一般位置直线的投影特性:
- 三个投影均不反映实长{三个投影的长度都小于实长}
- 三个投影均与投影轴倾斜
- 投影与投影轴的夹角均不反映空间直线对投影轴的倾角
2.投影面平行线
只平行于一个投影面,并与另外两投影面倾斜的直线,称为投影面的平行线。
依直线所平行的投影面不同,投影面平行面可分为:
- 水平线——只平行于H面的直线;(贝塔、伽马)
- 正平线——只平行于V面的直线;(阿尔法、伽马)
- 侧平线——只平行于W面的直线。(阿尔法、贝塔)
投影面平行线的投影特性:
- 在直线所平行的投影面上的投影,反映空间直线的实长,且与属于该投影面的两投影轴倾斜,与此两投影轴的夹角反映空间直线与另外两投影面的倾角。
- 在另外两投影面的上的投影平行于相应的投影轴,其投影长度均小于实长,其投影长度可反映该直线与所平行的投影面的距离。
图!
3.投影面垂直线
与投影面垂直的直线称为投影面垂直线。
垂直于一个投影面的直线,必平行于其余两个投影面,也平行于其余两投影面所共有的投影轴。
依直线所垂直的投影面不同,投影面垂直线可分为:
- 铅垂线——与H面垂直的直线;
- 正垂线——与V面垂直的直线;
- 侧垂线——与W面垂直的直线。
投影面垂直线的投影特性:
- 在直线所垂直的投影面上的投影为一点,即积聚性。其投影位置可反映该直线与另外两投影面的距离。
- 在另外两投影面上的投影垂直于相应的投影轴,并反映空间直线的实长。
图!
投影面平行线和投影面垂直线统称为特殊位置直线。其判断方法为:只要有一投影平行投影轴,即为特殊位置直线;另一投影积聚为一点,则为该投影面的垂直线;或另有一投影倾斜投影轴,则为该投影面的平行线。
4.1.3 一般位置直线的实长及倾角
一般位置直线的三个投影既不反映实长,也不反映空间直线与任何投影面的倾角。但是可以根据直线的投影,按一定的几何关系,通过图解的方法求得该直线的实长及对投影面的倾角。工程上常用直角三角形法。
求实长及倾角的方法:
- 以已知的某一投影为一直角边;
- 过该投影的某一端点作垂线,端点为垂足;在垂线上截取长度等于另一投影的对应坐标差,从而确定另一直角边;
- 连接两直角边的端点,即为斜边;
- 所得的直角三角形就是空间直角三角形的实形,斜边为原直线的实长,则斜边与选定的投影夹角即为所求的倾角。
图!
直角三角形图解一般位置线段实长与倾角的相互关系
各个直角三角形的4个几何元素中,知二可求二——
图!
4.2|直线上的点
4.2.1 直线上点的投影特性
由投影的从属性可知,点属于直线,则点的各面投影必属于直线的同面投影。 反之,若点的三个投影均分别属于直线的三个投影,则该点属于直线。
由投影定比性可知,满足从属性的点,分线段之比其投影后保持不变。
作图时要注意,不是给投影定比,而是另作一条线段来定比!
当侧平线未知第三W面投影时,不能判断点是否属于一条直线。
此时要采用作第三投影或者利用定比性来验证。
4.2.2 直线的迹点
直线与投影面的交点称为该直线的迹点,它属于直线的特殊点。
在三面投影体系中,一般位置直线由三个迹点,投影面平行线只有两个迹点,投影面垂直线只有一个迹点。
迹点分类:
- 水平迹点M
- 正面迹点N
- 侧面迹点S
迹点的投影特点:
迹点的投影具有直线上点和投影面上点的共同特点;
- 迹点的投影
如果对你有帮助的话不要忘记一键三连噢~
谢谢鸭~
初次编写于2021/2/17日;