机器学习--序言

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

例如：这是我对上学期机器学习知识总结，内容涵盖西瓜书和统计学习方法的部分内容。

---

序论

什么是机器学习

机器学习以数据为经验的载体，利用经验数据不断提高性能的计算机系统/程序/算法。机器学习是归纳（Induction）思维方式：从个别到一般。利用经验（数据）进行泛化推广至一般的算法或者程序。

机器学习部分术语

示例(instance) 数据集中的一个样本
标签(label) 示例结果的信息，例如“好瓜”，称为标记
属性(attribute) 反映事物或对象在某方面的表现或性质的事项，如“色泽”，称为属性或特征
特征(feature) 同属性
样例(sample) 同示例
测试样本(testing sample)
学得模型后，使用其进行预测的过程称为测试，被预测的样本称为测试样本
训练样本(training sample)
学习模型时，使用的示例
经验风险(empirical risk) 模型预测函数关于训练集的平均损失
结构风险()
奥卡姆剃刀(Occam’s razor) 若有多个假设与观察一致，则选最简单的那个

基本分类

根据数据标签类型分类

监督学习

监督学习（supervised learning）指从标注数据中学习预测模型的机器学习方法。
人话：数据有标签标注。
例如：线性模型的训练集中，已知各维度$x_i$和偏置$b$的取值，我们知道这组数据的对应输出值$y$

常见模型有：线性模型，决策树，支持向量机，感知机等等。

无监督学习

无监督学习（unsupervised learning）是指从无标签数据中学习预测模型的机器学习问题。
人话：数据没有标签标注。
例如：在聚类算法中，数据没有标签，我们甚至不知道模型要学习什么，在算法的引导下进行学习数据特征。

常见模型有：聚类

半监督学习

半监督学习是指利用少量带标签的数据和大量无标签数据学习预测模型的机器学习问题。
人话：少量数据有标签。大部分数据无标签。

根据任务类型分类

可分为

• 回归任务，标记为连续值。如得到一个瓜的成熟度。
• 分类任务，标记为离散值。如将一个瓜分为好瓜和坏瓜。
• 聚类任务，无标记。对瓜进行自动分组。

过拟合与欠拟合

过拟合是一味追求提高对训练数据的预测能力，导致得到的模型过于复杂的现象。
欠拟合则是模型复杂度不够导致。

对学习样本一般性质的程度进行区分。

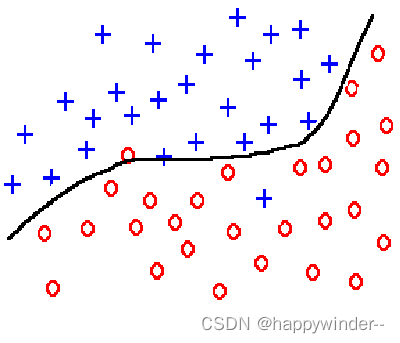
               goodfit

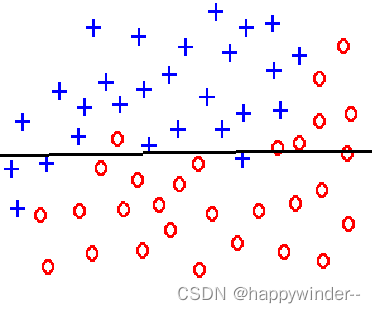
       underfitting(欠拟合)

       overfitting(过拟合)

过拟合常见解决方法

• Early Stopping (当发现有过拟合现象就停止训练)
• Penalizing Large Weight (在经验风险上加一个正则化项)
• Bagging 思想 (对同一样本用多个模型投票产生结果)
• Boosting 思想 (多个弱分类器增强分类能力，降低偏差)
• Dropconnection (神经网络全连接层中减少过拟合的发生)

欠拟合解决办法

• 决策树 ：拓展分支
• 神经网络 ：增加训练轮数
• 支持向量机：增加惩罚项

正则化

正则化是结构风险最小化策略的实现，是在经验风险上增加一个正则化项。正则化项一般是随模型复杂度单调递增的函数。

范数

定义$L_p$范数
$||x|{|}_p=\sqrt[p]{{\sum }_i|x_i{|}^p}$
因此$L0$范数用于统计向量中非零元素个数，$L1$范数就是向量各元素绝对值之和，$L2$范数用于表示向量或者矩阵的算术平方和，又称为欧氏距离。

为什么正则化可以缓解过拟合

       正则化会使模型偏好于更小的权值。更小的权值意味着更低的模型复杂度；添加 正则化相当于为模型添加了某种先验条件，这个先验条件限制了参数的分布，从而降低了模型的复杂度。
       模型的复杂度降低，意味着模型对于噪声与异常点的抗干扰性的能力增强，从而提高模型的泛化能力

$L1$正则化更容易找到稀疏解

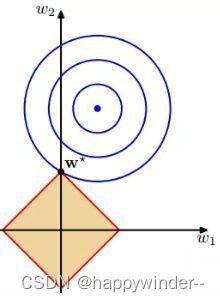
                                                                        L1正则化

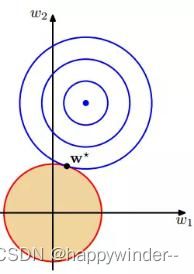
                                                                        L2正则化
因为L1正则化在零点附近具有很明显的棱角，L2正则化则在零附近比较平缓。所以L1正则化更容易使参数为零，L2正则化则减小参数值。

评估方法

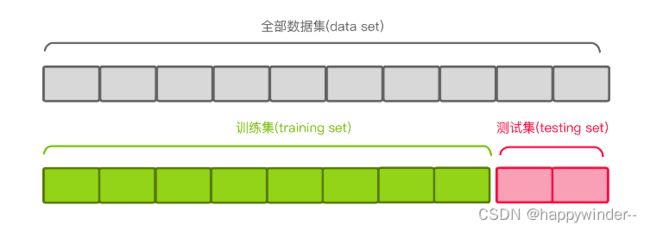
如果我们把数据集中所有的数据都拿去训练模型，那么就没有剩余数据进行模型的精度验证，所以我们在平时学习工作时会留出一部分数据，用于验，模型精度。

留出法(hand-out)

• 直接将数据集划分为两个互斥集合：训练集和测试集
• 训练/测试集划分要尽可能保持数据分布的一致性
• 分层采样(stratified sampling）：保持类别比例一致
• 一般若干次随机划分、重复实验取平均值
• 训练/测试样本比例通常为2:1~4:1，效果还不错

交叉验证(cross validation)

将数据集分层采样划分为k个大小相似的互斥子集，每次用k-1个子集的并集作为训练集，余下的子集作为测试集，最终返回k个测试结果的均值，k通常取值10

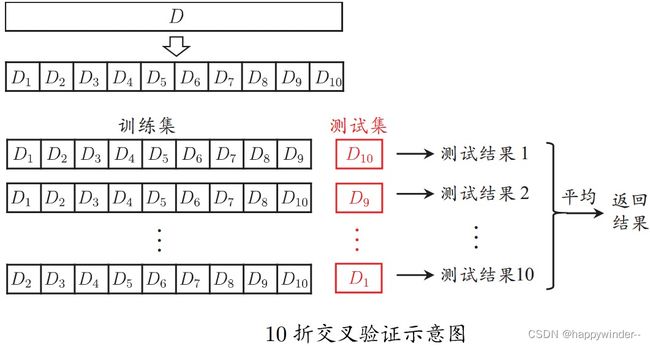
重复进行k次交叉验证–k折交叉验证，用于检验模型的泛化能力

自助法(bootstrap)

有放回抽样。

• 以自助采样法为基础，对数据集$D$有放回采样$m$次得到训练集$D^{\ast }$,$D\backslash D^{\ast }$用做测试集。
• 训练集$D^{\ast }$中样本有重复，约有1/3的样本没在训练集$D^{\ast }$中出现
• 实际模型与预期模型都使用m个训练样本
• 从初始数据集$D$中产生多个不同的训练集$D^{\ast }$，对集成学习有很大的好处

性能度量

错误率和精度

对于分类任务，错误率和精度是最常用的两种性能度量：

• 错误率：分错样本占样本总数的比例
• 精度：分对样本占样本总数的比率
  $E(f;D)=\frac{1}{m}{\sum }_i^m\mathbb{I}(f(x_i)\ne y_i)$
  $acc(f;D)=1-E(f;D)$

混淆矩阵、查准率、查全率

查准率$P=\frac{TP}{TP+FP}$
查全率$R=\frac{TP}{TP+FN}$

PR曲线

根据学习器的预测结果按正例可能性大小对样例进行排序，并逐个把样本作为正例进行预测，则可以得到查准率-查全率曲线，简称“P-R曲线”

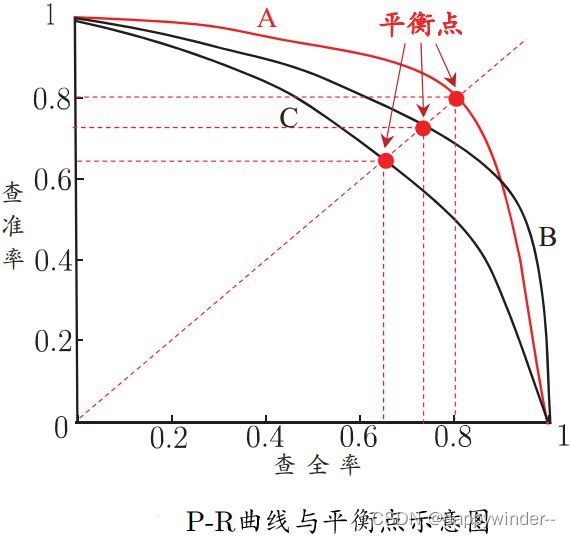
平衡点是曲线上“查准率=查全率”时的取值，可用来用于度量P-R曲线有交叉的分类器性能高低。

F度量

$F_{\beta }=\frac{(1+\beta {)}^2\times P\times R}{({\beta }^2\times P)+R}$
当$\beta =1$，就是$F1-score$

RUC曲线

类似P-R曲线，根据学习器的预测结果(置信度)对样例排序，并逐个作为正例进行预测，以“假正例率(FPR)”为横轴，“真正例率(TPR)”为纵轴可得到ROC曲线。

若某个学习器的ROC曲线被另一个学习器的曲线包住，则后者性能优于前者；否则如果曲线交叉，可根据ROC曲线下面积大小进行比较，也即AUC值。

偏差与方差

方差：使用同规模的不同训练集进行训练时带来的性能变化，刻画数据扰动带来的影响。
偏差：学习算法的期望预测与真实结果的偏离程度，刻画算法本身的拟合能力。

机器学习的目标

目标是使学得的模型能很好地适用于“新样本”，也就是强大的泛化能力。

---

总结

以上是对西瓜书术语和机器学习任务分类内容的概括。