基于matlab的边缘检测算法程序设计（含Canny算子）

概述

边缘可以认为是图像中一定数量点亮度发生变化的地方，边缘检测大体上就是计算这个亮度变化的导数（在离散数据中体现为差分），依据导数的大小，判断亮度变化大小，从而界定目标与背景。在经典的边缘检测算法中Roberts算子，Prewitt算子，Sobel算子属于一阶差分算子，LoG算子，Canny算子属于二阶差分算子。一阶差分算子，就是求图像灰度变化曲线的导数，从而可以突出图像中的对象边缘，而二阶差分算子，求图像灰度变化导数的导数，对图像中灰度变化强烈的地方很敏感，从而可以突出图像的纹理结构。Canny算子是在经典一阶算子边缘检测方法的思路上，同时继承了二阶LOG算子高斯平滑滤波的思想，并提出自己独特的根据梯度方向，对梯度幅值进行非极大值抑制的核心思路，集成以往边缘检测的优点，使得边缘检测效果迈上新的台阶。尽管Canny算子的提出已经是上个世纪的事情了，但它仍然在当前的数字图像处理中得到广泛应用，是公认的最优秀的边缘检测算法之一。

Roberts算子

Roberts算子是一种最简单的算子，是一种利用局部差分方式寻找边缘的算子。
定义水平方向梯度：
G_x=f(x+1,y+1)-f(x,y)
对应算子模板：

定义垂直方向梯度：
G_y=f(x+1,y)-f(x,y+1)
对应算子模板：

从算子模板来看，Roberts算子是一种斜向偏差分的梯度计算方法，梯度的大小代表边缘的强度，梯度的方向与边缘的走向垂直正交。
从图像处理的实际效果来看，2×2模板，计算简单，边缘定位较准，但正是因为采用了2×2模板，对于用关于中心点对称的模板来计算边缘方向不是很有用，对噪声极敏感，检测出的边缘轮廓线条较粗，可能有边缘缺失。适用于边缘明显且噪声较少的图像分割。
下边以这幅图片为例，根据Roberts算子原理编写算法实现函数myRoberts，将效果图与matlab自带edge（I,‘Roberts’）函数效果对比：

function [BW] = myRoberts(I,th)
%Roberts算子
if  ~exist('th','var') || isempty(th)
    th = 0.08;%假如阈值th不存在，默认阈值为0.08
end
if ndims(I) > 2
    grayI = rgb2gray(I);
else
    grayI = I;%判断是否为灰度图，不是则转为
end
[m,n]=size(grayI);
newI=grayI;
robertsNum=0;
for j=1:m-1
    for k=1:n-1
        robertsNum = abs(grayI(j,k)-grayI(j+1,k+1)) + abs(grayI(j+1,k)-grayI(j,k+1));
        if(robertsNum > th*255)
            newI(j,k)=255;
        else
            newI(j,k)=0;
        end
    end
end
BW = im2bw(newI);

前面两个if是为了提高函数的通用性，一是设置了默认的边缘阈值，一是匹配了rgb图像输入。重点的Roberts算法实现原理在下边的两重for循环中体现：对图片像素点进行遍历，根据上述Roberts算子定义的水平方向和垂直方向的梯度计算出大小，与设定的阈值比较。一般我们希望输入的阈值th是在0~1之间，而灰度图像素点采用8个比特位即255个灰度级来表示，故比较时th再乘上255.如果该点的梯度大于阈值，认定该点为梯度变化较大的位置即边缘，赋值为255.最后将灰度图转为二值图。
该函数使用效果（采用的默认阈值0.08）如下：
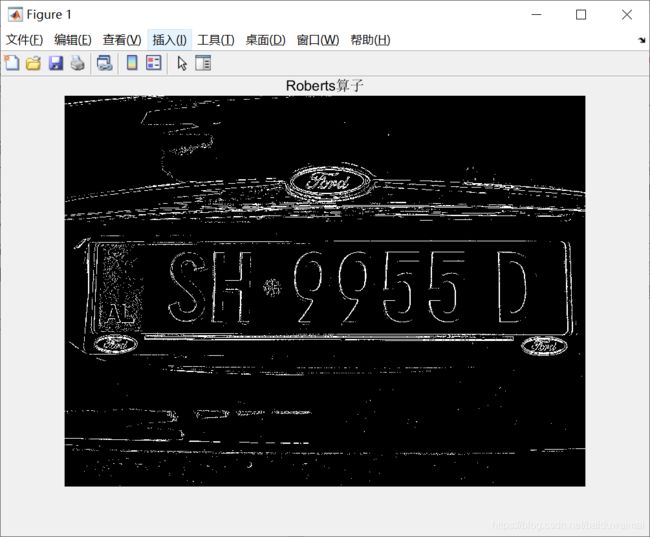而使用matlab自带函数效果如下：

Prewitt和Sobel

Prewitt和Sobel算子采用了3×3模板算子，在3×3模板中：

定义水平方向差分：
G_x=（Z_7+Z_8+Z_9 ）-（Z_1+Z_2+Z_3 ）
对应的算子模板：

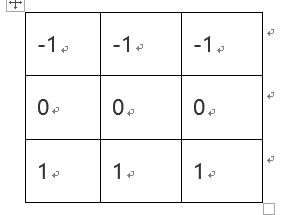
定义垂直方向差分：
G_y=（Z_3+Z_6+Z_9 ）-（Z_1+Z_4+Z_7 ）
对应的算子模板：

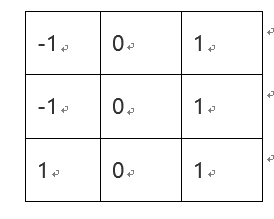
定义对角线方向差分：
G_x=（Z_2+Z_3+Z_6 ）-（Z_4+Z_7+Z_8 ）
G_y=（Z_6+Z_9+Z_8 ）-（Z_2+Z_1+Z_4 ）

Sobel算子是在Prewitt算子的基础上改进的，在中心系数上使用一个权值2，相比较Prewitt算子，Sobel模板能够较好的抑制（平滑）噪声。
由于采用了3*3模板，Prewitt算子的边缘检测结果在水平方向和垂直方向均比Robert算子更加明显。而Sobel算子结合了高斯平滑和一阶差分，在Prewitt算子的基础上增加了权重的概念，认为相邻点的距离远近对当前像素点的影响是不同的，距离越近的像素点对应当前像素的影响越大，从而实现图像锐化并突出边缘轮廓。

有了算子模板，算法实现方式与Roberts算子都是一致，只需按照模板定义的梯度公式稍加修改即可，在此不多赘述。

log算子

LoG(Laplacian of Gaussain)算法就是先对图像进行高斯平滑处理，再进行二阶差分的拉普拉斯算子锐化边缘。
高斯平滑算子：

二阶拉普拉斯方程：
∇^2 f(x，y)=(∂^2 f)/(∂^2 x)+(∂^2 f)/∂y
写成二维离散形式：
∇^2 f(x，y)=f（x+1，y）+f（x-1，y）+f（x，y+1）+f（x，y-1）-4f（x，y）
对应的二阶拉普拉斯算子模板：

下边仍以上图为例，根据log算子原理编写算法实现函数myLog，将效果图与matlab自带edge（I,‘log’）函数效果对比：

function [BW] = myLog(I,th)

if  ~exist('th','var') || isempty(th)
    th = 0.05;%假如阈值th不存在，默认阈值为0.08
end
if ndims(I) > 2
    grayI = rgb2gray(I);
else
    grayI = I;%判断是否为灰度图，不是则转为
end
gauss = [1 2 1; 2 4 2;1 2 1] / 16;  % Gauss平滑模板
grayI = conv2(grayI, gauss, 'same');   % 平滑
[m,n]=size(grayI);
newI=grayI;
LogNum=0;
for j=2:m-1
    for k=2:n-1
        LogNum = abs(4*grayI(j,k)-grayI(j-1,k)-grayI(j+1,k)-grayI(j,k+1)-grayI(j,k-1));
        if(LogNum > th*255)
            newI(j,k)=255;
        else
            newI(j,k)=0;
        end
    end
end
BW = im2bw(newI);

与上述算子的算法不同点在于遍历像素点之前做了以高斯平滑算子与图像卷积实现了高斯平滑滤波。梯度计算时采用的是二阶拉普拉斯算子。
效果图如下;

matlab自带函数效果图如下：

Canny算子

从表面效果上来讲，Canny算法是对Sobel、Prewitt等算子效果的进一步细化和更加准确的定位，同时借鉴了LoG算子先进行高斯滤波（噪声平滑）再进行图像梯度计算的思想。
关于Canny算法实现请参考我的这篇博文：
基于matlab的Canny算法实现（附源代码）