22-变分推断-variational inference

1.背景

关于变分推断，现在补充一点背景知识，以便让每一个模块都很独立。我们指导机器学习可以分为频率派和贝叶斯派两大派系，关于这两个派系都有各自不同的特点。

1.1 频率派

我们知道从频率派角度来看，最终会演化为一个优化问题。比如我们熟悉的回归问题

1.1.1 回归问题

假设我们有一堆数据$D=\{(x_i,y_i){\}}_{i=1}^N,x_i\in R^P,y_i\in R;$,我们定义的模型为：
$$f(x)=W^{T}X\text{\hspace{1em}(1)}$$

• 定义一条线，我们需要结合数据X把W估计出来。
  为了更好的拟合上述数据，我们提出了损失函数Loss Function：
  $$L(W)=\sum _{i=1}^N||w^T{x}_i-y_i|{|}^2\text{\hspace{1em}(2)}$$
  最后估计出来的w用$\hat{w}$表示：
  $$\hat{w}=\underset{w}{\mathrm{argmin}}L(W)\text{\hspace{1em}(3)}$$

• 这是一种无约束的优化问题。
  求解上述优化问题我们有两种方法：

• 解析解：
  $$\frac{\partial L(W)}{\partial w}=0\to W^{\ast }=(X^{T}X{)}^{-1}{X}^{T}Y\text{\hspace{1em}(4)}$$

• 数值解：
  当解析解无法求解的时候，我们用梯度下降的方式求解GD,或者用随机梯度下降的方式求解SGD

1.1.2 SVM支持向量机(分类问题)

SVM支持向量机本质上就是一个分类问题。我们定义SVM的模型为：
$$f(w)=sign(w^{T}x+b)\text{\hspace{1em}(5)}$$
我们定义SVM支持向量机的Loss Function损失函数为：
$$L(W)=\frac{1}{2}{w}^{T}w;s.t:y_i(w^T{x}_i+b)\ge 1,i=1,2,...,N\text{\hspace{1em}(6)}$$

• 这是一个约束问题，也是一个凸优化问题。
  解法是用QP套件或者用拉格朗日对偶来求解。

1.1.3 EM

EM算法也是一种优化问题的思想，通过不停的迭代，来找到最好的参数：迭代公式如下：
$${\theta }^{(t+1)}=\underset{\theta }{\mathrm{argmax}}{\int }_z\log P(X,Z|\theta )\cdot P(Z|X,{\theta }^{(t)})dz\text{\hspace{1em}(7)}$$

• 故EM算法也是一个迭代优化问题

1.2 贝叶斯派

我们知道从频率派角度来看，最终会演化为一个积分问题。由贝叶斯公式可得：
$$P(\theta |X)=\frac{P(X|\theta )\cdot P(\theta )}{P(X)}\text{\hspace{1em}(8)}$$

• $P(\theta |X):后验$
• $P(X|\theta ):似然$
• $P(\theta ):先验$
• $P(X)={\int }_{\theta }P(X|\theta )\cdot P(\theta )d\theta ：对参数空间X的积分$
  贝叶斯推断指的是在贝叶斯框架中需要把后验的分布$P(\theta |X)$求出来；贝叶斯决策就可以简单的理解为预测的意思。假设X为已经有的N个样本，$\hat{X}$为新的样本，决策的目标是为了求$P(\hat{X}|X)$的值，为了求得新的$\hat{X}$,那么我们就会引入一个新的参数$\theta ；使得$
  $$\hat{X}\to \theta \to X\text{\hspace{1em}(9)}$$
  从而转变为如下公式：
  $$P(\hat{X}|X)={\int }_{\theta }P(\hat{X},\theta |X)d\theta ={\int }_{\theta }P(\hat{X},\theta |X)\cdot P(\theta |X)d\theta =E_{\{\theta |X\}}[P(\hat{X}|\theta )]\text{\hspace{1em}(10)}$$
  所以最终的目标是求后验$P(\theta |X)$,也就是推断inference。
  常见的推断分为两种：
• 精确推断
• 近似推断
  1.确定性近似推断:比如：VI 变分推断
  2.随机性近似推断：比如 MCMC，MH,Gibbs

2.公式推导

变分推断VI的目的就是想办法找到一个分布q(z)去逼近我们没有办法计算求得解析解的后验分布p(z|x).我们定义

• $X:observed-data观测数据；$
• $Z：latent-variable+parameter隐变量$
• $(X,Z):complete-data完整数据$
  现在我们来根据贝叶斯公式来求导后验分布：
  由贝叶斯公式可得：

$P(X)=\frac{P(X,Z)}{P(Z|X)}=\frac{P(X,Z)/q(Z)}{P(Z|X)/q(Z)}$

两边取对数可得：

$\log P(X)=\log [P(X,Z)/q(Z)]-\log [P(Z|X)/q(Z)]$

两边同时对分布q(Z)求期望：

左边：

${\int }_{q(z)}\log P(X)dZ={\int }_Z\log P(X)q(Z)dZ=\log P(X){\int }_{Z}q(Z)dZ=\log P(X)$

右边：
$$\underset{ELBO}{{\int }_{Z}q(Z)\log \frac{P(X,Z)}{q(Z)}dZ}+\underset{KL(q||p)}{{\int }_Z(-q(Z)\log \frac{P(Z|X)}{q(Z)}dZ)}\text{\hspace{1em}(11)}$$
则：
$$\log P(X)=\underset{ELBO=L(q)}{{\int }_{Z}q(Z)\log \frac{P(X,Z)}{q(Z)}dZ}+\underset{KL(q||p)}{{\int }_Z(-q(Z)\log \frac{P(Z|X)}{q(Z)}dZ)}\text{\hspace{1em}(12)}$$
我们定义一个函数L(q)来代替ELBO，用来说明ELBO的输入是关于q的函数，q是我们随意找到的概率密度函数，其中函数L(q)就是我们的所指的变分。由于我们求不出P(Z|X),我们的目的是找到一个q(Z),使得P(Z|X)近似于q(Z)，也就是希望KL(q||p)越来越小，这样我们求得的ELBO越接近于$\log P(X)$,那么我们的目标可以等价于：
$$\widehat{q(Z)}=\underset{q(Z)}{\mathrm{argmax}}L(q)\to \widehat{q(Z)}\approx p(Z|X)\text{\hspace{1em}(13)}$$

2.1平均场理论

为了求解q(Z),因为Z是一组隐变量组成的随机变量组合。我们假设q(Z)可以划分为M个组，且每个组之间是相互独立的。这种思想来自于物理学的平均场理论，表达如下：
$$q(Z)=\prod _{i=1}^M{q}_i(Z_i)\text{\hspace{1em}(14)}$$
平均场理论主要思想如下：
现在我们把q(Z)代入到L(q)中，因为q(Z)有M个划分，我们的想法是先求解第j项，所以我们需要固定其他所有项(固定$\{1,2,...,j-1,j+1,...,M\}$).这样我们就一个一个求解$q_j$后再求积得到q(Z)即可。

• 将q(Z)代入到L(q)中
  $$L(q)=\underset{1}{{\int }_{Z}q(Z)\log P(X,Z)dZ}-\underset{2}{{\int }_{Z}q(Z)\log q(Z)dZ}\text{\hspace{1em}(15)}$$
  $1={\int }_Z{\prod }_{i=1}^M{q}_i(Z_i)\log P(X,Z)d{Z}_{1}d{Z}_2...d{Z}_M$

$={\int }_{Z_j}{q}_j(Z_j)d{Z}_j\cdot [{\prod }_{i=1,且i\ne j}^M{q}_i(Z_i)\log P(X,Z)d{Z}_{1}d{Z}_{2}d{Z}_{j-1}d{Z}_{j+1}..d{Z}_M]$

$={\int }_{Z_j}{q}_j(Z_j)d{Z}_j\cdot {\int }_{Z_i;i=1,...j-1,j+1,...M}\log P(X,Z){\prod }_{i\ne j}^M{q}_i(Z_i)d{Z}_i$

$={\int }_{Z_j}{q}_j(Z_j)\cdot E_{{\prod }_{i\ne j}^M{q}_i(Z_i)}[\log P(X,Z)]d{Z}_j$

$2={\int }_{Z}q(Z)\log q(Z)dZ$

$={\int }_Z{\prod }_{i=1}^M{q}_i(Z_i)\log {\prod }_{i=1}^M{q}_i(Z_i)dZ$

$={\int }_Z{\prod }_{i=1}^M{q}_i(Z_i)[{\sum }_{i=1}^M\log q_i(Z_i)]dZ$

将求和展开后拿出第一项目进行分析：

$第一项={\int }_Z{\prod }_{i=1}^M{q}_i(Z_i)\log q_1(Z_1)]dZ$

$={\int }_{Z_1}{q}_1(Z_1)\log q_1(Z_1)d{Z}_1\cdot \underset{=1}{{\int }_{Z_2...Z_M}\prod _{i=2}^M{q}_i(Z_i)d{Z}_2...d{Z}_M}={\int }_{Z_1}{q}_1(Z_1)\log q_1(Z_1)d{Z}_1$
同理可得：

$2={\int }_Z{\prod }_{i=1}^M{q}_i(Z_i)[{\sum }_{i=1}^M\log q_i(Z_i)]dZ$

$={\int }_{Z_1}{q}_1(Z_1)\log q_1(Z_1)d{Z}_1+{\int }_{Z_2}{q}_2(Z_2)\log q_2(Z_2)d{Z}_2+...+{\int }_{Z_M}{q}_M(Z_M)\log q_M(Z_M)d{Z}_M$

$={\sum }_{i=1}^M{\int }_{Z_i}{q}_i(Z_i)\log q_i(Z_i)d{Z}_i$
由于我们现在只关心第j项目，其他项目已经固定，所以上式可变为如下：

$2={\int }_{Z_j}{q}_j(Z_j)\log q_j(Z_j)d{Z}_j+C_{常数}$
综上所述：
我们发现1和2中的式子不一致，不方便化简，所以我们希望1中的式子也跟2中的log保持一致，这样就方便后续计算，所以我们定义如下：
因为：

$1={\int }_{Z_j}{q}_j(Z_j)\cdot E_{{\prod }_{i\ne j}^M{q}_i(Z_i)}[\log P(X,Z)]d{Z}_j$

为方便后续计算，转换如下：

$1={\int }_{Z_j}{q}_j(Z_j)\cdot \log \hat{P}(X,Z_j)d{Z}_j$

又因为：
$2={\int }_{Z_j}{q}_j(Z_j)\log q_j(Z_j)d{Z}_j+C_{常数}$

$L(q)=1-2={\int }_{Z_j}{q}_j(Z_j)\cdot \log \frac{\hat{P}(X,Z_j)}{q_j(Z_j)}d{Z}_j-C=-KL(q_j(Z_j)||\hat{P}(X,Z_j))-C_{常数}$
又由于我们要求最值问题，所以尝试C可以忽略，只关心KL项即可。

$L(q)=1-2=-KL(q_j(Z_j)||\hat{P}(X,Z_j))\le 0$

• 当$q_j(Z_j)=\hat{P}(X,Z_j)\cdot C_{常数}时，上式不等式取等号.$

3.再回首

我们已经讲解了基于平均场理论的变分推断，即：(VI-mean field),也称经典推断classical VI；

• 假设将q(Z)分为M份，且M份之间是相互独立的，这个假设比较强：
  $$Assumption:q(Z)=\prod _{i=1}^M{q}_i(Z_i)\text{\hspace{1em}(16)}$$
• 结论：
  $$\log q_j(Z_j)=E_{i\ne j,q_i(Z_i)}[\log P(X,Z|\theta )]+CONS{T}_{常数}\text{\hspace{1em}(17)}$$
• =${\int }_{q_1}{\int }_{q_2}...{\int }_{q_{j-1}}{\int }_{q_{j+1}}...{\int }_{q_M}{q}_1{q}_2...q_{j-1}{q}_{j+1}[\log P(x^{(i)},z]d_{q_1}...d_{q_{j-1}}{d}_{q_{j+1}}...d_{q_M}+CONS{T}_{常数}$
• 可以看出上述公式展开后就式一个迭代式。将上述公式迭代可得如下：
• $\widehat{q_1}(z_1)={\int }_{q_2}...{\int }_{q_M}{q}_2...q_M[\log P(x^{(i)},z]d_{q_2}......d_{q_M}$
• $\widehat{q_2}(z_2)={\int }_{{\hat{q}}_1}{\int }_{q_3}...{\int }_{q_M}{\hat{q}}_1{q}_3...q_M[\log P(x^{(i)},z]d_{{\hat{q}}_1}{d}_{q_3}...d_{q_M}$
• …
• $\widehat{q_M}(z_M)={\int }_{{\hat{q}}_1}...{\int }_{{\hat{q}}_{M-1}}{\hat{q}}_1...{\hat{q}}_{M-1}[\log P(x^{(i)},z]d_{{\hat{q}}_1}{d}_{{\hat{q}}_2}...d_{{\hat{q}}_{M-1}}$

这种迭代方式就跟坐标上升法算法一样的思想。以上是一个经典的基于平均场理论的变分推断方法，但这种方法也有缺点

• 这种平均分割q(z)为M份的假设太强了。对于某些简单模型是可以实现的，但对于一些复杂的模型来说是不能成立的。比如深度玻尔兹曼机和深度神经网络就没法切割成相互独立的M份。
• 即使假设M份是成立的，但是对于复杂模型来说，$\log q_j(Z_j)=E_{i\ne j,q_i(Z_i)}[\log P(x^{(i)},z]$积分也是非常难求出来的。

变分推断说到底还是推断，推断在概率图模型中指的往往是求后验是什么，EM和变分推断在推导过程中用的是同一套理论(ELBO)。只是处理问题有些不同而已。因为变分推断关心的是后验，所以我们应该弱化参数$\theta$.
$$\log P_{\theta }(X)=\underset{L(q)}{ELBO}+\underset{\ge 0}{KL(q||p)}\ge L(q)\text{\hspace{1em}(18)}$$

• 为了求最大的$\log P_{\theta }(X)$,我们其实就是为了求ELBO中最大的q(z),KL(q||p)中最小的q；
  $$\hat{q}=\underset{q}{\mathrm{argmin}}KL(q||p)=\underset{q}{\mathrm{argmax}}L(q)\text{\hspace{1em}(19)}$$
• 这样我们就将一个求后验的变分问题转换成一个优化问题.

3.1 符号规范

为了以后更加方便描述数学问题，我们定义用小写表示随机变量：

• x：observed - variable 观测随机变量
• z：latent - variable 隐含随机变量
• $x_i：表示维度$
• $x^{(i)}：表示第i个x样本;X=\{x^{(i)}{\}}_{i=1}^N$
• $z^{(i)}：表示第i个z样本;Z=\{z^{(i)}{\}}_{i=1}^N$
  我们假设每个样本$x^{(i)}$之间是满足独立同分布的。所以可得如下：
  $$\log P_{\theta }(X)=\log \prod _{i=1}^N{P}_{\theta }(x^{(i)})=\sum _{i=1}^N\log P_{\theta }(x^{(i)})\text{\hspace{1em}(20)}$$
• 我们的目标是求得最大的$\log P_{\theta }(X)$,所以我们的想法是只需要求得每一个$\log P_{\theta }(x^{(i)})$最大值即可。所以我们的研究对象变成了$\log P_{\theta }(x^{(i)})$
  $$ELBO=E_{q(z)}[\log \frac{P_{\theta }(x^{(i)}z)}{q(z)}]=E_{q(z)}[\log P_{\theta }(x^{(i)},z)]+H[q(z)]\text{\hspace{1em}(21)}$$
  $$KL(q||p)=\int q(z)\cdot \log \frac{q(z)}{P_{\theta }(z|x^{(i)})}dz\text{\hspace{1em}(22)}$$
• 注：这里的$z_i$不是指一个数据维度的集合，而指的是一个类似的最大团的概念。也就是多个维度结合在一起。

4. SGVI-随机梯度变分推断

4.1求梯度${\nabla }_{\varphi }L(\varphi )$

Stochastic Gradient Variational Inference简称SGVI算法，即随机梯度变分推断算法。对于Z和X组成的模型，我们常常按如下方式区分生成模型和推断模型。

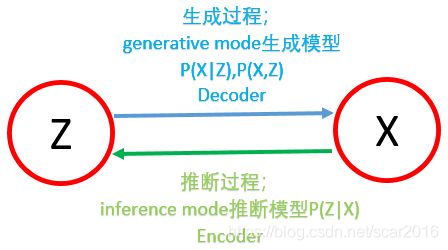
我们上一节分析了基于平均场理论的变分推断，通过平均假设得到了变分推断的结论。可以看到它是一种坐标上升法的思想去处理问题，那么，既然坐标上升法能够处理变分推断问题，那么我们也可以用梯度上升法来解决这个问题，这样我们就自然而然地想到了随机梯度变分推断SGVI。我们知道对于随机梯度算法来说，它的更新是需要方向和步长的，满足如下公式：
$${\theta }^{(t+1)}={\theta }^{(t)}+{\lambda }^{(t)}\nabla L(q)\text{\hspace{1em}(23)}$$

• 注：这样我们只需要求得$\nabla L(q)$即可；
• 由于q是关于z和x的概率分布，即q(z|x)在这里我们通篇是忽略x 的，因为x是观测变量，为了简化起见，我们用q(z)表示q(z|x),我们令q(z)是一个指数族分布，那么为了求q(z)这个分布，本质上是为了求关于分布q(z)所需的参数$\varphi$，所以我们令所求的分布为$q_{\varphi }(z)$，所以我们的目标函数可以化简为如下：
  $$ELBO=E_{q_{\varphi }(z)}[\log \frac{P_{\theta }(x^{(i)}z)}{q_{\varphi }(z)}]=E_{q_{\varphi }(z)}[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]=L(\varphi )\text{\hspace{1em}(24)}$$
  $$L(\varphi )=E_{q_{\varphi }(z)}[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\text{\hspace{1em}(25)}$$
  整理上式可得目标函数为：
  $$\hat{\varphi }=\underset{\varphi }{\mathrm{argmax}}L(\varphi )=\underset{\varphi }{\mathrm{argmax}}{E}_{q_{\varphi }(z)}[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\text{\hspace{1em}(26)}$$
  $对上式关于\varphi 求导，我们令\frac{\partial L(\varphi )}{\partial \varphi }={\nabla }_{\varphi }L(\varphi )$:
  $${\nabla }_{\varphi }L(\varphi )={\nabla }_{\varphi }{E}_{q_{\varphi }(z)}[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\text{\hspace{1em}(27)}$$
  具体步骤如下：

${\nabla }_{\varphi }L(\varphi )={\nabla }_{\varphi }{E}_{q_{\varphi }(z)}[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]$

$={\nabla }_{\varphi }\{{\int }_z{q}_{\varphi }(z)\cdot [\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]dz\}$

• 注：d(AB)=d(A)B+Ad(B),积分号与求导符号互换位置。

$={\int }_z[\underset{d(A)}{{\nabla }_{\varphi }\{q_{\varphi }(z)\}}\cdot \underset{B}{\{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}}]dz$

$+{\int }_z[\underset{A}{\{q_{\varphi }(z)\}}\cdot \underset{d(B)}{{\nabla }_{\varphi }\{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}}]dz$

我们对于上式分开解析：

$1={\int }_z[{\nabla }_{\varphi }\{q_{\varphi }(z)\}\cdot \{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}]dz$

$2={\int }_z[\{q_{\varphi }(z)\}\cdot {\nabla }_{\varphi }\{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}]dz$

$我们知道：\log P_{\theta }(x^{(i)}z)与\varphi 无关,故导数为0.$

$2={\int }_z[\{q_{\varphi }(z)\}\cdot {\nabla }_{\varphi }\{\underset{与\varphi 无关}{[\log P_{\theta }(x^{(i)},z)}-\log q_{\varphi }(z)]\}]dz$
$2={\int }_z[\{q_{\varphi }(z)\}\cdot {\nabla }_{\varphi }\{-\log q_{\varphi }(z)\}]dz$

$={\int }_z[\{q_{\varphi }(z)\}\cdot {\nabla }_{\varphi }\{-\log q_{\varphi }(z)\}]dz$

$=-{\int }_z[\{q_{\varphi }(z)\}\cdot \frac{1}{q_{\varphi }(z)}{\nabla }_{\varphi }\{q_{\varphi }(z)\}]dz$

$=-{\int }_z[{\nabla }_{\varphi }\{q_{\varphi }(z)\}]dz$

$=-{\nabla }_{\varphi }{\int }_z[\{q_{\varphi }(z)\}]dz$

$=-{\nabla }_{\varphi }\underset{=1}{{\int }_z[\{q_{\varphi }(z)\}]}dz$

$=-{\nabla }_{\varphi }1=0$

结论：
$${\nabla }_{\varphi }L(\varphi )={\int }_z[{\nabla }_{\varphi }\{q_{\varphi }(z)\}\cdot \{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}]dz\text{\hspace{1em}(28)}$$

• 因为${\nabla }_{\varphi }\{q_{\varphi }(z)\}=q_{\varphi }(z){\nabla }_{\varphi }\log \{q_{\varphi }(z)\},故上式可变如下：$
  $${\nabla }_{\varphi }L(\varphi )={\int }_z[q_{\varphi }(z){\nabla }_{\varphi }\log \{q_{\varphi }(z)\}\cdot \{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}]dz\text{\hspace{1em}(29)}$$

• 转换成关于分布$q(\varphi )$的期望形式：

结论：
$${\nabla }_{\varphi }L(\varphi )=E_{\{q_{\varphi }(z)\}}[{\nabla }_{\varphi }\log \{q_{\varphi }(z)\}\cdot \{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}]\text{\hspace{1em}(30)}$$

• 所以我们的梯度可以用一个期望表示，这样我们用蒙特卡罗的方式近似求得期望，最后得到梯度。
  将上述得到的梯度代入如下公式即可得到梯度法求解的迭代公式：
  $${\theta }^{(t+1)}={\theta }^{(t)}+{\lambda }^{(t)}\nabla L(q)\text{\hspace{1em}(31)}$$

4.2 梯度采样

我们已经把梯度转换成期望的公式，现在就是如何求这个期望，们采用的是蒙特卡罗采样法，具体步骤如下：

• $假设z^l来自于分布即：z^l\sim q_{\varphi }(z)；l=1,2,..,L,那么可得如下：$
• $${\nabla }_{\varphi }L(\varphi )\approx \frac{1}{L}\sum _{l=1}^L[{\nabla }_{\varphi }\log \{q_{\varphi }(z^{(l)})\}\cdot \{\log P_{\theta }(x^{(i)},z^{(l)})-\log q_{\varphi }(z^{(l)})\}]\text{\hspace{1em}(32)}$$
  对于上式最大的问题是，当我们在$q_{\varphi }(z)$中采样的时候，会有概率采到$q_{\varphi }(z)$在某一个时刻非常的小，所以就会导致$|\log \{q_{\varphi }(z^{(l)})\}|$会非常的大,从而出现方差较大的情况(high variance)，当方差越大的时候，就会出现需要更多的样本L去平衡方差，那么现实过程中就出现无法采样的现象发生。即：
  $$\underset{q_{\varphi }(z)->0}{\lim }\log \{q_{\varphi }(z^{(l)})\}=\infty \text{\hspace{1em}(33)}$$
  为了解决因方差较大时，上述无法采样的现象，我们提出新的方法重参数化技巧[Reparameterization Trick]

4.3 重参数化技巧

重参数化技巧的核心思想是对$q_{\varphi }(z)$进行简化，假设我们得到一个确定的解$P(ϵ)$,那么我们就很容易解决上述期望不好求的问题。

$${\nabla }_{\varphi }L(\varphi )={\nabla }_{\varphi }{E}_{\{q_{\varphi }(z)\}}[\log \{q_{\varphi }(z)\}\cdot \{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}]\text{\hspace{1em}(34)}$$

注：因为z来自于$q_{\varphi }(z)$,如果我们能够想办法将z中的随机变量分离出来，将 z 的随机性用另外一个变量$ϵ$表示出来，我们定义一个函数，表示变量$ϵ$与随机变量z之间的关系：
$$z=g_{\varphi }(ϵ,x^{(i)})\to ϵ\sim P(ϵ)\text{\hspace{1em}(36)}$$

• 这样做的好处是：不再是连续的关于$\varphi$的采样了，可以有效的降低方差，并且，z是关于$ϵ$的函数，我们将随机性转移到了$ϵ$中，那么上述问题可以简化为如下：
  $$z\sim q_{\varphi }(z|x^{(i)})\to ϵ\sim p(ϵ)\text{\hspace{1em}(37)}$$
  我们引入如下等式：
  $$|q_{\varphi }(z|x^{(i)})dz|=|p(ϵ)dϵ|\text{\hspace{1em}(38)}$$

由于$z=g_{\varphi }(ϵ,x^{(i)})$是一个函数关系，即映射关系，那么我们可以知道发生z的概率跟发生$ϵ$的概率一致;
我们令PA为发生z的概率，故$PA=q_{\varphi }(z|x^{(i)})dz$;同理令PB为发生$ϵ$的概率$PB=p(ϵ)dϵ$,故可得：
$$PA=|q_{\varphi }(z|x^{(i)})dz|=PB=|p(ϵ)dϵ|\text{\hspace{1em}(39)}$$
现在我们根据上述公式更新梯度:
$${\nabla }_{\varphi }L(\varphi )={\nabla }_{\varphi }{\int }_z[\{q_{\varphi }(z)\}\cdot \{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}]dz\text{\hspace{1em}(40)}$$
$$={\nabla }_{\varphi }{\int }_z[\{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}]\{q_{\varphi }(z)\}dz\text{\hspace{1em}(41)}$$
$$={\nabla }_{\varphi }{\int }_z[\{[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\}]p(ϵ)dϵ\text{\hspace{1em}(42)}$$
$$={\nabla }_{\varphi }{\int }_{ϵ}[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]p(ϵ)dϵ\text{\hspace{1em}(43)}$$
$$={\nabla }_{\varphi }{E}_{\{P_{ϵ}\}}[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\text{\hspace{1em}(44)}$$
$$=E_{\{P_{ϵ}\}}{\nabla }_{\varphi }[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]\text{\hspace{1em}(45)}$$
$$=E_{\{P_{ϵ}\}}{\nabla }_z[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z)]{\nabla }_{\varphi }z\text{\hspace{1em}(46)}$$

• 我们之前定义了$q_{\varphi }(z)=q_{\varphi }(z|x^{(i)});z=g_{\varphi }(ϵ,x^{(i)})$
  $${\nabla }_{\varphi }L(\varphi )=E_{\{P_{ϵ}\}}\{{\nabla }_z[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z|x^{(i)})]\}\cdot {\nabla }_{\varphi }{g}_{\varphi }(ϵ,x^{(i)})\text{\hspace{1em}(47)}$$
  那么我们的关于期望的采样就简化了很多，因为$p(ϵ)$与$\varphi$无关，我们可以先求$[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z|x^{(i)})]$关于z的导数，然后再求$g_{\varphi }(ϵ,x^{(i)})$关于$\varphi$的导数，这三者之间是相互分离开的，最后我们对结果进行采样，可得：
  $${ϵ}^{(l)}\sim p(ϵ);l=1,2,..,L\text{\hspace{1em}(48)}$$
  经过上述公式转换后的期望，因函数简化后，我们可以用蒙特卡洛的方法进行采样了。
  $${\nabla }_{\varphi }L(\varphi )\approx \frac{1}{L}\sum _{i=1}^L[\{{\nabla }_z[\log P_{\theta }(x^{(i)},z)-\log q_{\varphi }(z|x^{(i)})]\}\cdot {\nabla }_{\varphi }{g}_{\varphi }(ϵ,x^{(i)})]\text{\hspace{1em}(49)}$$

• 其中$z=g_{\varphi }({ϵ}^{(i)},x^{(i)}),最后将上式的值代入迭代公式即可：$
  $${\theta }^{(t+1)}={\theta }^{(t)}+{\lambda }^{(t)}{\nabla }_{\varphi }L(\varphi )\text{\hspace{1em}(50)}$$
  证毕。