搭建深度学习框架（七)：softmax+交叉熵损失函数的实现

上一节已经实现了LSTM网络的搭建，这一节将实现交叉熵损失函数的搭建和运用，实现对物体的分类。
代码下载地址：xhpxiaohaipeng/xhp_flow_frame
一、softmax+交叉熵损失函数代码实现的原理
1.在经过交叉熵损失函数处理前，输出结果应先经过一个softmax函数处理得到一个总和为1的概率分布。
softmax函数实现如下：

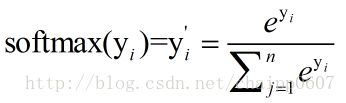
那么softmax函数对y求导，可得导数为：

softmax(y)-softmax(y)**2

2.最终将softmax函数的结果输入交叉熵损失函数计算损失。
交叉熵的原理
交叉熵刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。假设概率分布p为期望输出，概率分布q为实际输出，H(p,q)为交叉熵，则：
交叉熵损失函数实现如下：

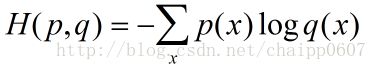
这个公式如何表征距离呢，举个例子：
假设N=3，期望输出为p=(1,0,0)，实际输出q1=(0.5,0.2,0.3)，q2=(0.8,0.1,0.1)，那么：

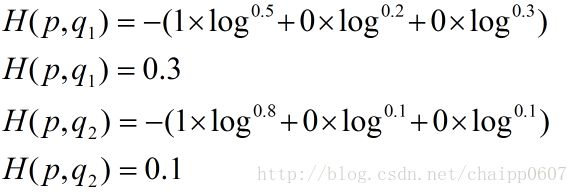
很显然，q2与p更为接近，它的交叉熵也更小。p为实际类别（0或1），q为softmax函数的计算值。
实际上交叉熵损失函数的p(x)可直接等于1,q(x)的值对应于p(x)的类别的概率值。
最终根据链式法则可得交叉熵损失函数的导数为：

q(x) -1

二、softmax+交叉熵损失函数代码实现
代码实现如下：

class EntropyCrossLossWithSoftmax(Node):
    def __init__(self, y_pre, y_label,alpha=0.01, name='EntropyLossWithSoftmax', is_trainable=False):
        Node.__init__(self, [y_pre, y_label], name=name, is_trainable=is_trainable)
        self.y_pre = self.inputs[0]
        self.y_label = self.inputs[1]
        """
        prevent the np.exp(x) to nan
        """
        self.softmax_alpha = alpha

        assert alpha <= 1,'alpha should not be biger than 1'

    def softmax(self, L):

        EXEP = np.exp(L)
        SUM = np.sum(EXEP, axis=1)
        for i in range(len(L)):
            for k in range(len(L[i])):
                L[i][k] = EXEP[i][k] / SUM[i]
        return L

    def cross_entropy_error(self,y_, y):

        if y_.ndim == 1:
            y = y.reshape(1, y.size)
            y_ = y_.reshape(1, y_.size)

        if y.size == y_.size:
            y = y.argmax(axis=1)

        self.result = y_.argmax(axis=1)
        self.y_bool = self.result == y
        self.accuracy = np.mean(self.y_bool)

        batch_size = y.shape[0]
        """
        prevent taking the log of 0
        """
        eps = np.finfo(float).eps
        """
        #y_[np.arange(batch_size), y]代表选择每一行
        代表的所有类别里面的正确类别此时的概率,然后所有
        概率的对数值的相反数相加就是交叉熵损失
        """
        return -np.mean(np.log(y_[np.arange(batch_size), y] + eps))

    def forward(self):

        self.y = self.y_label.value
        """
        self.softmax_alpha 防止np.exp(x)的值倾向于无穷大
        """
        self.y_ = self.softmax(self.softmax_alpha*self.y_pre.value)
        self.value = self.cross_entropy_error(self.y_, self.y)

    def backward(self):

        batch_size = self.y.shape[0]
        if self.y.size == self.y_.size:
            dx = (self.y_ - self.y) / batch_size
        else:
            """
            sottmax(x)函数对x的导数为sottmax(x) - softmax(x)*sottmax(x)
            """
            dx = self.y_.copy()
            dx[np.arange(batch_size), self.y] -= 1

        self.gradients[self.y_pre] = self.softmax_alpha*dx
        self.gradients[self.y_label] = -self.softmax_alpha*dx

        if self.gradients[self.y_pre].ndim == 3:
            self.gradients[self.y_pre] = np.mean(self.gradients[self.y_pre],axis=1,keepdims=False)
            self.gradients[self.y_label] = np.mean(self.gradients[self.y_label],axis=1,keepdims=False)

最后使用MLP+交叉熵损失函数对一个车辆的直行、左右转弯行为进行分类。
代码实现如下：

import os
from xhp_flow.nn.node import Placeholder,Linear,Sigmoid,ReLu,Leakrelu,Elu,Tanh,LSTM
from xhp_flow.optimize.optimize import toplogical_sort,run_steps,forward,save_model,load_model,Auto_update_lr,Visual_gradient,Grad_Clipping_Disappearance,SUW,\
SGD,\
Momentum,\
Adagrad,\
RMSProp,\
AdaDelta,\
Adam,\
AdaMax,\
Nadam,\
NadaMax

from xhp_flow.loss.loss import MSE,EntropyCrossLossWithSoftmax
import matplotlib.pyplot as plt

os.environ['CUDA_LAUNCH_BLOCKING'] = "1"


def labeltoint(label):
    if label == 'left':
        label = 0
    if label == 'keep':
        label = 1
    if label == 'right':
        label = 2
    return label


import json
import numpy as np

with open('data1/train.json', 'r') as f:
    j = json.load(f)
    #  print(j.keys())
    X_train = j['states']
    Y_train = j['labels']
    for i in range(len(Y_train)):
        Y_train[i] = labeltoint(Y_train[i])
#  print(Y_train)

with open('data1/test.json', 'r') as f:
    j = json.load(f)
    X_test = j['states']
    Y_test = j['labels']
    for i in range(len(Y_test)):
        Y_test[i] = labeltoint(Y_test[i])

split_frac = 0.8
X_train, Y_train, X_test, Y_test = np.array(X_train).astype(np.float32), np.array(Y_train).astype(np.long), np.array(  \
    X_test).astype(np.float32), np.array(Y_test).astype(np.long)

## split data into training, validation, and test data (features and labels, x and y)
val_x, test_x = X_test[:len(X_test) // 2], X_test[len(X_test) // 2:]
val_y, test_y = Y_test[:len(Y_test) // 2], Y_test[len(Y_test) // 2:]

import torch
from torch.utils.data import TensorDataset, DataLoader

# create Tensor datasets
train_data = TensorDataset(torch.from_numpy(X_train), torch.from_numpy(Y_train))
valid_data = TensorDataset(torch.from_numpy(val_x), torch.from_numpy(val_y))
test_data = TensorDataset(torch.from_numpy(test_x), torch.from_numpy(test_y))

# dataloaders
batch_size = 64

# make sure to SHUFFLE your data
train_loader = DataLoader(train_data, shuffle=True, batch_size=batch_size)
valid_loader = DataLoader(valid_data, shuffle=True, batch_size=batch_size)
test_loader = DataLoader(test_data, shuffle=True, batch_size=batch_size)

x1, y = next(iter(train_loader))
input_x, y = x1.numpy(), y.numpy()


class MLP_classify():
    def __init__(self, input_size=4, hidden_size=16, output=3):
        self.x, self.y = Placeholder(name='x', is_trainable=False), Placeholder(name='y', is_trainable=False)
        self.w1, self.b1 = Placeholder(name='w1'), Placeholder(name='b1')
        self.w2, self.b2 = Placeholder(name='w2'), Placeholder(name='b2')
        self.w3, self.b3 = Placeholder(name='w3'), Placeholder(name='b3')
        self.w_out, self.b_out = Placeholder(name='w3'), Placeholder(name='b3')

        self.output1 = Linear(self.x, self.w1, self.b1, name='linear1')
        self.output2 = ReLu(self.output1, name='sigmoid')
        self.output3 = Linear(self.output2, self.w2, self.b2, name='linear2')
        self.output4 = ReLu(self.output3, name='Relu')
        self.output5 = Linear(self.output4, self.w3, self.b3, name='linear3')
        self.y_pre = Linear(self.output5, self.w_out, self.b_out, name='linear3')
        self.cross_loss = EntropyCrossLossWithSoftmax(self.y_pre, self.y,0.01,name='cross_en')

        # 初始化数据结构
        self.feed_dict = {
            self.x: input_x,
            self.y: y,
            self.w1: np.random.rand(input_size, hidden_size),
            self.b1: np.zeros(hidden_size),
            self.w2: np.random.rand(hidden_size, hidden_size),
            self.b2: np.zeros(hidden_size),
            self.w3: np.random.rand(hidden_size, hidden_size),
            self.b3: np.zeros(hidden_size),
            self.w_out: np.random.rand(hidden_size, output),
            self.b_out: np.zeros(output)
        }


mlp_class = MLP_classify(4, 16, 3)


# graph_mlp_class = convert_feed_dict_graph(mlp_class.feed_dict)
# print(graph_sort_class)
def train(model, train_data, epoch=4000, learning_rate=0.00128):
    # 开始训练
    accuracies = []
    losses = []
    losses_valid = []
    accuracies_valid = []
    loss_min = np.inf
    graph_sort_class = toplogical_sort(model.feed_dict)  # 拓扑排序
    optim = Nadam(graph_sort_class)
    update_lr = Auto_update_lr(lr=learning_rate, alpha=0.1, patiences=500, print_=True)
    for e in range(epoch):
        for X, Y in train_data:
            X, Y = X.numpy(), Y.numpy()
            model.x.value = X
            model.y.value = Y
            run_steps(graph_sort_class)
            optim.update(learning_rate=learning_rate)
            Visual_gradient(model)
            Grad_Clipping_Disappearance(model, 5)
            loss = model.cross_loss.value
            accuracy = model.cross_loss.accuracy
            losses.append(loss)
            accuracies.append(accuracy)
        for x, y in valid_loader:
            x, y = x.numpy(), y.numpy()
            model.x.value = x
            model.y.value = y
            run_steps(graph_sort_class, train=False, valid=True)
            loss_valid = model.cross_loss.value
            accuracy_valid = model.cross_loss.accuracy
            losses_valid.append(loss_valid)
            accuracies_valid.append(accuracy_valid)
        update_lr.updata(np.mean(losses_valid))
        print("epoch:{}/{},train loss:{:.8f},train accuracy:{:.8f},valid loss:"\
            "{:.8f},valid accuracy:{:.8f}".format(e,epoch,np.mean(losses),
        np.mean(accuracies), np.mean(losses_valid),np.mean(accuracies_valid)))
        if np.mean(losses_valid) < loss_min:
            print('loss is {:.6f}, is decreasing!! save moddel'.format(np.mean(losses_valid)))
            save_model("model/mlp_class.xhp", model)
            loss_min = np.mean(losses_valid)

    plt.plot(losses)
    plt.savefig("image/mlp_class_loss.png")
    plt.show()

def predict(x,model):
    graph = toplogical_sort(model.feed_dict)
    model.x.value = x
    run_steps(graph,train=False,valid=False)
    y = graph[-2].value
    result = np.argmax(y,axis=1)

    return result



def evaluator(test_loader,model):
    graph = toplogical_sort(model.feed_dict)
    accuracies = []
    losses = []
    for x, y in test_loader:
        x, y = x.numpy(), y.numpy()
        model.x.value = x
        model.y.value = y
        run_steps(graph, train=False, valid=True)
        loss_test = model.cross_loss.value
        accuracy_test = model.cross_loss.accuracy
        losses.append(loss_test)
        accuracies.append(accuracy_test)
    print("test loss:{},test accuracy:{}".format(np.mean(losses),np.mean(accuracies)))

#load_model('model/mlp_class.xhp',mlp_class)
train(mlp_class, train_loader, 50000,0.001)
x1,y = next(iter(train_loader))
input_x,y = x1.numpy(),y.numpy()
load_model('model/mlp_class.xhp',mlp_class)
classs = predict(input_x[0][None,:],mlp_class)
print(classs,y[0])
evaluator(test_loader,mlp_class)

最后得到的验证集的准确率为95.6%，测试集的准确率为96.9%。