Transformer架构：位置编码

2017年，Google的Vaswani 等人提出了一种新颖的纯注意力序列到序列架构，闻名学术界与工业界的 Transformer 架构横空出世。它的可并行化训练能力和优越的性能使其成为自然语言处理领域（Natural Language Processing，NLP）以及计算机视觉领域（Computer Vision，CV）研究人员的热门选择。本文将重点讨论Transformer架构一个不可或缺的部分——位置编码（Positional Encoding）。

Transformer架构

位置编码是什么？它为什么这么重要？

在人类的语言中，单词的位置与顺序定义了语法，也影响着语义。无法捕获的单词顺序会导致我们很难理解一句话的含义，如下图所示。

因此在NLP任务中，对于任何神经网络架构，能够有效识别每个词的位置与词之间的顺序是十分关键的。传统的循环神经网络（RNN）本身通过自回归的方式考虑了单词之间的顺序。然而Transformer 架构不同于RNN，Transformer 使用纯粹的自注意力机制来捕获词之间的联系。纯粹的自注意力机制具有置换不变的性质（证明请见）。换句话说，Transformer中的自注意力机制无法捕捉输入元素序列的顺序。因此我们需要一种方法将单词的顺序合并到Transformer架构中，于是位置编码应运而生。

位置编码的作用方式

目前，主流的位置编码方法主要分为绝对位置编码与相对位置编码两大类。其中绝对位置编码的作用方式是告知Transformer架构每个元素在输入序列的位置，类似于为输入序列的每个元素打一个"位置标签"标明其绝对位置。而相对位置编码作用于自注意力机制，告知Transformer架构两两元素之间的距离。如下图所示。

绝对位置编码

最早的绝对位置编码起源于2017年Jonas Gehring等人发表的Convolutional Sequence to Sequence Learning，该工作使用可训练的嵌入形式作为位置编码。随后Google的Vaswani等人在Attention Is All You Need文章中使用正余弦函数生成的位置编码。关于Transformer架构为什么选择正余弦函数去生成绝对位置编码以及正余弦函数的一些特性，笔者安利大家阅读kazemnejad老师的博文《Transformer Architecture: The Positional Encoding》，该文详细叙述了正余弦绝对位置编码的原理。诞生于 2018 年末的 BERT也采用了可训练的嵌入形式作为编码。实际上，这三项工作的共性都是在每个词的嵌入上加位置编码之后输入模型。形式上，如下公式所示：
$$x=(w_1+p_1,...,w_m+p_m).$$
其中，$x$表示模型的输入，$w_m$表示第$m$个位置的词嵌入，$p_m$表示第$m$个位置的绝对位置编码。

近年来，关于绝对位置编码的工作大多数是以不同的方法生成绝对位置编码为主。下面列出一些关于绝对位置编码的一些工作，感兴趣的同学可以了解一下~

1. Learning to Encode Position for Transformer with Continuous Dynamical Model
   该文提出一种基于连续动态系统的绝对位置编码（FLOATER），从数据中学习神经微分方程递归生成位置编码，在机器翻译、自然语言理解和问答等任务上获得了不错的性能提升。
   由于递归机制本身具有出色的外推性质，所以FLOATER基本不受文本长度的限制。并且作者说明了正余弦绝对位置编码就是FLOATER的一个特解。该工作在WMT14 En-De和En-Fr分别进行了实验，分别对比Transformer Base模型有着0.4和1.0 BLEU值的涨幅。但与此同时，这种递归形式的位置编码也牺牲了原本模型的并行输入，在速度上会有一定影响。
2. Encoding Word Order in Complex Embeddings
   该工作提出一种复值词向量函数生成绝对位置编码，巧妙地将复值函数的振幅和相位与词义和位置相联系，在机器翻译、文本分类和语言模型任务上获得了不错的性能提升。。
   该复值词向量函数以位置为变量，计算每个词在不同位置的词向量。由于该函数对于位置变量而言是连续的，因此该方法不光建模了绝对位置，也建模了词之间的相对位置。该工作在WMT16 En-De机器翻译任务数据集上进行了实验，复值词向量对比Transformer Base模型有1.3 BLEU值的涨幅。
3. SHAPE: Shifted Absolute Position Embedding for Transformers
   该工作提出了一种绝对位置编码的鲁棒性训练方法。作者认为现有的位置编码方法在测试不可见长度时缺乏泛化能力，并提出了平移绝对位置编码(SHAPE)来解决这两个问题。SHAPE的基本思想是在训练过程中对绝对位置编码随机整体平移一段距离来实现泛化能力。该工作在WMT16 En-De机器翻译任务数据集上进行训练，将newstest2010-2016作为校验集和测试集，对比正余弦绝对位置编码，该方法有着一定的性能提升。

相对位置编码

最经典的相对位置编码起源于Shaw等人发表的Self-Attention with Relative Position Representations。在介绍相对位置表示之前，首先简要介绍一下自注意力机制的计算流程，对于Transformer模型的某一自注意力子层：
$$\begin{gathered} Q=x{W}_Q \\ K=x{W}_K \\ V=x{W}_V \end{gathered}$$
其中，$x$为上一层的输出，$W_Q$、$W_K$、$W_V$为模型参数，它们可以通过自动学习得到。此时，对于整个模型输入的向量序列$x=\{x_1,\dots ,x_m\}$，通过点乘计算，可以得到当前位置$i$和序列中所有位置间的关系，记为$z_i$，计算公式如下：
$$z_i=\sum _{j=1}^m{\alpha }_{ij}(x_j{W}_V)$$
这里，$z_i$可以被看做是输入序列的线性加权表示结果。而权重${\alpha }_{ij}$通过Softmax函数得到：
$${\alpha }_{ij}=\frac{\exp (e_{ij})}{{\sum }_{k=1}^m\exp (e_{ik})}$$
进一步，$e_{ij}$被定义为：
$$e_{ij}=\frac{(x_i{W}_Q){(x_j{W}_K)}^{\text{T}}}{\sqrt{d_k}}$$
其中，$d_k$为模型中隐藏层的维度。$e_{ij}$实际上就是$Q$和$K$的向量积缩放后的一个结果。而相对位置表示的核心思想就是在$z_i$与$e_{ij}$的计算公式里面分别引入了可学习的相对位置向量$a_{ij}^V$与$a_{ij}^K$。改进后的自注意力机制如下：
$$\begin{array}{rl}{z}_i& =\sum _{j=1}^m{\alpha }_{ij}(x_j{W}_V+a_{ij}^V)\\ e_{ij}& =\frac{x_i{W}_Q{(x_j{W}_K+a_{ij}^K)}^{\text{T}}}{\sqrt{d_k}}\\ & =\frac{x_i{W}_Q{(x_j{W}_K)}^{\text{T}}+x_i{W}_Q{(a_{ij}^K)}^T}{\sqrt{d_k}}\end{array}$$
其中，$a_{ij}^V$与$a_{ij}^K$定义如下：
$$\begin{array}{rl}{a}_{ij}^K& =w_{\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}(j-i,k)}^K\\ a_{ij}^V& =w_{\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}(j-i,k)}^V\\ \mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}(x,k)& =\mathrm{m}\mathrm{a}\mathrm{x}(-k,\mathrm{m}\mathrm{i}\mathrm{n}(k,x))\end{array}$$
通过预先设定的最大相对位置$k$，强化模型对以当前词为中心的左右各$k$个词的注意力计算。因此，最终的窗口大小为$2k+1$。对于边缘位置窗口大小不足$2k$的单词，采用了裁剪的机制，即只对有效的临近词进行建模。相对位置权重$a_{ij}$矩阵如下图所示：

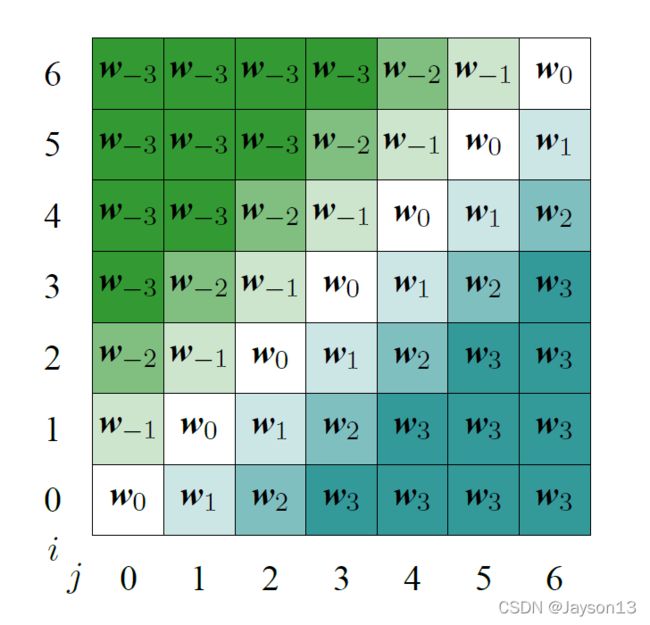
由Self-Attention with Relative Position Representations引出了一系列相对位置编码的讨论与改进。
下面列出一些关于相对位置编码的一些工作，感兴趣的同学可以了解一下~

1. Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context
   该文改进相对位置编码的动机源于如下公式的完全展开，分别表示单词-单词、位置-位置、单词-位置、位置-单词：
   $$\begin{array}{rl}{e}_{ij}& =\frac{(x_i{W}_Q){(x_j{W}_K)}^{\text{T}}}{\sqrt{d_k}}\\ & =\frac{((w_i+p_i)W_Q){(w_j+p_j)W_K)}^{\text{T}}}{\sqrt{d_k}}\\ & =\frac{w_i{W}_Q{W_K}^T{w_j}^T+p_i{W}_Q{W_K}^T{p_j}^T+w_i{W}_Q{W_K}^T{p_j}^T+p_i{W}_Q{W_K}^T{w_j}^T}{\sqrt{d_k}}\end{array}$$
   作者认为单词-位置、位置-单词这两部分是不合理的。该文将$p_j$替换为相对位置向量$R_{i-j}$，与Shaw的训练式的相对位置向量不同，本文使用正余弦编码生成$R_{i-j}$。$p_i$替换为两个可训练的向量$u,v$，公式如下：
   $$\begin{array}{r}{e}_{ij}=\frac{w_i{W}_Q{W_K}^T{w_j}^T+v{W}_Q{W_K}^T{R_{i-j}}^T+w_i{W}_Q{W_K}^T{R_{i-j}}^T+u{W}_Q{W_K}^T{w_j}^T}{\sqrt{d_k}}\end{array}$$
   Transformer-XL提出的片段级别递归和相对位置编码使模型具有学习长距离依赖的能力，加速效果很明显并且可以支持的最长依赖近似于O(NL)。Google 随后提出的XLNet模型也采用了Transformer-XL的结构。
2. Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer
   相较于Transformer-XL，Google提出的预训练语言模型T5所使用的相对位置编码更为简单。该工作将位置-位置、单词-位置、位置-单词替换成一个可以学习的偏置项，如下公式：
   $$\begin{array}{r}{e}_{ij}=\frac{w_i{W}_Q{W_K}^T{w_j}^T+{\alpha }_{i-j}}{\sqrt{d_k}}\end{array}$$
   值得一提的是，对于相对位置偏置项${\alpha }_{i-j}$，T5模型采用了更精细的分段处理。在相对距离较近的情况下（相对距离窗口为-7~7），每个位置使用独立训练的相对位置向量；而随着相对距离的增加（相对距离窗口小于-7或大于7），多个位置会共享一个相对位置向量，直至相对距离达到阈值进行clip操作。
3. Rethinking Positional Encoding in Language Pre-training
   文章指出了当下基于Transformer结构的预训练模型中位置编码存在的两个问题。第一个问题便是上述单词-位置、位置-单词的对应问题。其次，作者认为符号[CLS]不应当含有位置信息。基于此作者移除了单词-位置、位置-单词的对应关系，同时引用T5模型中的偏置项：
   $$\begin{array}{r}{e}_{ij}=\frac{w_i{W}_Q{W_K}^T{w_j}^T}{\sqrt{2d_k}}+\frac{p_i{U}_Q{U_K}^T{p_j}^T}{\sqrt{2d_k}}+{\alpha }_{i-j}\end{array}$$
   其中，$U_Q$与$U_K$为可学习的参数矩阵。同时把[CLS]标识符的位置信息抹除使得任何其它位置与其有着相同的相对位置关系。作者在GLUE(General Language Understanding Evaluation)任务上进行了实验，证明了这两部分改进的有效性。
4. DeBERTa: Decoding-enhanced BERT with Disentangled Attention
   与前三个工作相比，微软提出的预训练语言模型DeBERTa所使用的相对位置编码机制也是类似。该工作将展开式调整成如下公式：
   $$\begin{array}{r}{e}_{ij}=\frac{w_i{W}_Q{W_K}^T{w_j}^T+w_i{W}_Q{W_K}^T{R_{i-j}}^T+R_{j-i}{W}_Q{W_K}^T{w_j}^T}{\sqrt{d_k}}\end{array}$$
   本文中，$R_{i-j}$与Shaw的工作一样都是训练式可截断的相对位置向量。同时，DeBERTa指出相对位置信息对于大多数NLP任务更加重要，但绝对位置信息在某些任务上也很重要。
5. RoFormer: Enhanced Transformer with Rotary Position Embedding
   与前面工作的“套路”截然不同，作者苏剑林提出一种旋转式位置编码，利用绝对位置编码实现相对位置编码的效果。具体方法为：
   $$\begin{array}{r}{e}_{ij}=\frac{w_i{W}_Q{R}_i{R_j}^T{W_K}^T{w_j}^T}{\sqrt{d_k}}=\frac{w_i{W}_Q{R}_{i-j}{W_K}^T{w_j}^T}{\sqrt{d_k}}\end{array}$$
   其中，$R_{i-j}$为正交的旋转矩阵。在进行Attention计算时，将$Q_i$和$K_j$视为高维空间上的点，分别乘以对应的旋转矩阵，根据其绝对位置$i$与$j$分别对其逆时针旋转对应的角度。这样，在进行内积运算后的数值与相对位置$i-j$相关。因此这种位置编码方法有非常直观的物理含义，同时这也是一种可用于线性Attention的相对位置编码。
6. Improve Transformer Models with Better Relative Position Embeddings
   该文作者针对Shaw等人的相对位置编码提出了四种改进方法，分别如下：
   $$\begin{array}{rl}{e}_{ij}& =\frac{(x_i{W}_Q){(x_j{W}_K)}^{\text{T}}{\alpha }_{|i-j|}}{\sqrt{d_k}}\\ e_{ij}& =\frac{(x_i{W}_Q){(x_j{W}_K)}^{\text{T}}{\alpha }_{i-j}}{\sqrt{d_k}}\\ e_{ij}& =\frac{\mathrm{s}\mathrm{u}\mathrm{m}\_\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{d}(x_i{W}_Q,x_j{W}_K,{\alpha }_{i-j})}{\sqrt{d_k}}\\ e_{ij}& =\frac{(x_i{W}_Q+{\alpha }_{i-j})(x_j{W}_K+{\alpha }_{i-j})-<{\alpha }_{i-j},{\alpha }_{i-j}>}{\sqrt{d_k}}\end{array}$$
   从公式上来看，与Shaw的相对位置编码相比，前三种改进方法取消了将相对位置信息附加在Key元素上的做法，以乘法的方式融合了相对位置信息。而最后一种方法将相对位置信息同时附加在了Query和Key元素上，并减去了两个相对位置嵌入相乘的结果。那么最终便是Query-Key、Query-相对位置、相对位置-Key这三项的相加。对比Shaw多了相对位置-Key这个对应关系，笔者认为这么做还是很有趣的。作者在SQuAD1.1数据集上面进行了实验，与训练式和正余弦的绝对位置编码以及Shaw的相对位置编码进行比较，性能有一定的提升。并通过实验证明了方法的外推性和鲁棒性。

关于位置编码的分析性工作

1. Analysis of Positional Encodings for Neural Machine Translation
   该文章主要针对机器翻译任务，根据不同句子长度的测试集，对比分析了绝对位置编码与相对位置编码的性能，用实验证明了相对位置编码更具有优势，泛化能力更加强大。

2. What Do Position Embeddings Learn? An Empirical Study of Pre-Trained Language Model Positional Encoding
   文章提供一个新的视角，说明在不同NLP任务上应使用不同的位置编码。

3. On Position Embeddings in BERT
   文章在多项NLP任务上对不同的位置编码进行了定性分析。

参考

1. 让研究人员绞尽脑汁的Transformer位置编码
2. 机器翻译：基础与模型
3. Transformer Architecture: The Positional Encoding
4. 一文读懂Transformer模型的位置编码
5. Position Information in Transformers: an Overview