Zero-Reference Deep Curve Estimation for Low-Light Image Enhancement
Zero-Reference Deep Curve Estimation for Low-Light Image Enhancement
- 论文链接:https://arxiv.org/abs/2001.06826
- 有补充材料
- 期刊/会议:CVPR 2020
- 是否有code: Code
关键词
暗光图像增强,卖方法,无监督,实时;
问题简述&个人评价
Motiviation:作者观察到,在通过PS提亮图片时,用户往往是通过手工调整图片的亮度曲线来完成的(也就是“Curves Adjustment”)。本文顺着这个思路,直接用CNN来直接预测出一个亮度曲线,来完成图片的提亮。
Abstract:为了实现这个目的,本文设计了Deep Curve Estimation Network (DCE-Net),DCE-Net输入一张RGB的低光照图片,输出分别对应着R、G、B三个通道的三条Light-Enhancement Curve (LE-Curve)。值得一提的是,训练网络所用的loss是由好几个不需要参考图像就可以计算的子loss组成,因此第一次将无监督引入到了暗光增强过程中。这也是为什么本文叫做Zero-Reference,即不需要承成对的数据,甚至不需要不成对但有参考的数据。
本文的第一个创新点在于LE-Curve的引入:
本文采用了由浅及深的方式来介绍LE-Curve,使得复杂且抽象的概念逐渐变得清晰:
首先是LE-Curve最简单的版本,它需要满足三点要求:
- 增强图像的像素值归一化为[0,1],这避免了由于overflow truncation而导致的信息丢失;
- 设计的曲线应该是单调的,从而保留相邻像素间的差异(对比度);
- 曲线应该尽可能地简单,使得其在梯度反向传播过程中是可导的。
最简单版本的LE-Curve被设计成了下式:
L E ( I ( x ) ; α ) = I ( x ) + α I ( x ) ( 1 − I ( x ) ) (1) LE(I(x);\alpha)=I(x)+\alpha I(x)(1-I(x)) \tag{1} LE(I(x);α)=I(x)+αI(x)(1−I(x))(1)
其中,x为像素坐标,LE(I(x); α)为输入图像I(x)的增强结果,α∈[-1,1]为可训练的曲线参数(修改曲线的大小并控制曝光度)。每个像素都归一化为[0,1],并且所有操作都是pixel-wise。
值得注意的是,作者完全没有描述LE-Curve为什么被设计成这样,只是描述了公式1满足了一开始提到的那三个要求。这虽然让人有吐槽的欲望,但还挺值得借鉴的,首先省空间,第二避免说一大堆分析被打脸;
Higher-Order LE-Curve:
很容易想到将“迭代优化”的思路引入到LE-Curve中,这就是Higher-Order LE-Curve:
L E n ( x ) = L E n − 1 ( x ) + α n L E n − 1 ( x ) ( 1 − L E n − 1 ( x ) ) (2) LE_{n}(x)=LE_{n-1}(x)+\alpha_{n} LE_{n-1}(x)(1-LE_{n-1}(x)) \tag{2} LEn(x)=LEn−1(x)+αnLEn−1(x)(1−LEn−1(x))(2)
n代表着迭代的次数,作者发现n=8时表现就已经足够好了。
Pixel-Wise LE-Curve:
在上面两个公式中 α n \alpha_{n} αn 对于不同位置、不同亮度的像素点来说都是一样的,显然不够科学,很容易想到将 α n \alpha_{n} αn 从一个”值“延伸成一个“图”,类似于Attention的方式:
L E n ( x ) = L E n − 1 ( x ) + A n ( x ) L E n − 1 ( x ) ( 1 − L E n − 1 ( x ) ) (3) LE_{n}(x)=LE_{n-1}(x)+\mathcal{A}_{n}(x) LE_{n-1}(x)(1-LE_{n-1}(x)) \tag{3} LEn(x)=LEn−1(x)+An(x)LEn−1(x)(1−LEn−1(x))(3)
显然 A n \mathcal{A}_{n} An 就是“升级”版的 α n \alpha_{n} αn 。这里额外提一句,作者对这个升级给出了一个解释: α n \alpha_{n} αn 代表着global adjustment,而global adjustment很难去平衡 过曝和欠曝区域的提亮力度。因此要将global adjustment细化为local adjustment;
流程框图:
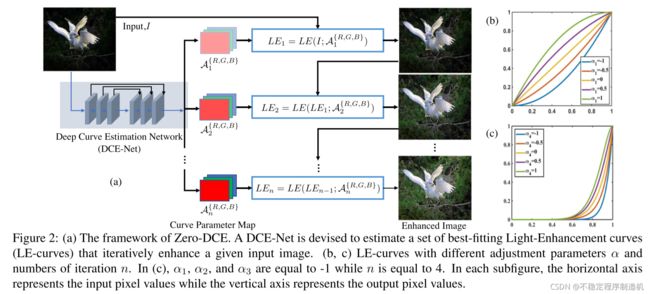
这个图画的还是比较清楚的,就是有一点没想明白:DCE-Net在迭代过程中每次吃的输入都是原始输入 I I I ?怎么想都感觉有问题,回来可能得去翻翻代码。
本文的第二个创新点在于Non-Reference Loss的设计:
L t o t a l = L s p a + L e x p + W c o l L c o l + W t v A L t v A (4) L_{total}=L_{spa} + L_{exp} + W_{col}L_{col} + W_{tv_{\mathcal{A}}} L_{tv_{\mathcal{A}}} \tag{4} Ltotal=Lspa+Lexp+WcolLcol+WtvALtvA(4)
L t o t a l L_{total} Ltotal 就是最终使用的loss, L s p a L_{spa} Lspa , L e x p L_{exp} Lexp , L c o l L_{col} Lcol , L t v A L_{tv_{\mathcal{A}}} LtvA 则分别代表着Spatial Consistency Loss,Exposure Control Loss,Color Constancy Loss,Illumination Smoothness Loss, W c o l W_{col} Wcol 与 W t v A W_{tv_{\mathcal{A}}} WtvA 则是对应loss前的系数,下面分别开始介绍各个loss的具体作用:
Spatial Consistency Loss
L s p a L_{spa} Lspa 的目的是维持增强前后图像的邻域间的对比度,避免经过pixel-wise的
输入图像与其增强版本之间的邻域差异(对比度),从而促进增强后图像仍能保持空间一致性。
L s p a = 1 K ∑ i = 1 K ∑ j ∈ Ω ( i ) ( ∣ ( Y i − Y j ) ∣ − ∣ ( I i − I j ) ∣ ) 2 (5) L_{spa} = \frac{1}{K} \sum_{i=1}^K \sum_{j\in \Omega(i)}(|(Y_{i}-Y_{j})|-|(I_{i}-I_{j})|)^2 \tag{5} Lspa=K1i=1∑Kj∈Ω(i)∑(∣(Yi−Yj)∣−∣(Ii−Ij)∣)2(5)
其中, K K K 为局部区域的数量, Ω ( i ) \Omega(i) Ω(i) 是以区域 i i i 为中心的四个相邻区域(上、下、左、右), Y Y Y 和 I I I 分别为增强图像和输入图像的局部区域平均强度值。这个局部区域的Size经验性地设置为 4 × 4 4\times4 4×4(loss对这个尺寸的值不敏感)。
Exposure Control Loss
L e x p L_{exp} Lexp 是用来控制曝光程度的loss,它可以有效地帮助 A n ( x ) \mathcal{A}_{n}(x) An(x) 将欠曝光和过曝光区域映射到一个适当的曝光成都。在这里,作者假设适当的曝光程度的定义是像素值的均值为 E E E,那么 L e x p L_{exp} Lexp 定义如下式:
L e x p = 1 M ∑ k = 1 M ∣ Y k − E ∣ (6) L_{exp} = \frac{1}{M} \sum_{k=1}^M|Y_{k}-E| \tag{6} Lexp=M1k=1∑M∣Yk−E∣(6)
M M M 为不重叠的局部区域数量,区域Size为16x16,Y为增强图像中局部区域的平均像素强度值。作者发现E的值在[0.4,0.7]的区间内对于结果的影响都不大,最终设置 为 E = 0.6 为E=0.6 为E=0.6 。
Color Constancy Loss
考虑到 A n ( x ) \mathcal{A}_{n}(x) An(x) 是分别独立应用于 R 、 G 、 B R、G、B R、G、B 三个通道的,如果不对三个通道增强后的图像加以限制,最终生成的结果往往会存在非常严重的色偏问题(serve color cast)。因此,基于Gray-World颜色恒等假设(关于Gray-World可以参照这篇博客)),设计了 L c o l L_{col} Lcol 来补偿这个问题。
L c o l = ∑ ∀ ( p , q ) ∈ ϵ ( J p − J q ) 2 , ϵ = { ( R , G ) , ( R , B ) , ( G , B ) } (7) L_{col} = \sum_{\forall(p,q) \in \epsilon} (J^p-J^q)^2 , \epsilon=\{(R,G),(R,B),(G,B)\} \tag{7} Lcol=∀(p,q)∈ϵ∑(Jp−Jq)2,ϵ={(R,G),(R,B),(G,B)}(7)
其中, J p J^p Jp 代表增强图像通道 p p p 的像素值的平均值, ( p , q ) (p, q) (p,q) 代表一对通道。
Illumination Smoothness Loss
L t v A L_{tv_{\mathcal{A}}} LtvA 则是为了照顾到三个要求中的“单调性”而设置的。先回顾一下LE-Curve,因为 α \alpha α 是固定的,所以LE-Curve一定能保证映射后的结果也一定是满足单调性要求的。但是在 Pixel-Wise LE-Curve 中,由于 A n ( x ) \mathcal{A}_{n}(x) An(x) 并不是固定的,如果不加以约束的话,是不一定能够保证映射后的结果还满足单调性要求的。作者在这里的处理也很简单,就是让 A n ( x ) \mathcal{A}_{n}(x) An(x) 尽量的去接近 α \alpha α,要求 A n ( x ) \mathcal{A}_{n}(x) An(x) 作为一张“图”,它的梯度尽可能小:
L t v A = 1 N ∑ i = 1 N ∑ c ∈ ξ ( ∣ ( ▽ x A n c ∣ + ∣ ▽ y A n c ∣ ) 2 , ξ = { R , G , B } (8) L_{tv_{\mathcal{A}}} = \frac{1}{N} \sum_{i=1}^N \sum_{c \in \xi}(|( \bigtriangledown_{x} \mathcal{A}_{n}^c | + | \bigtriangledown_{y} \mathcal{A}_{n}^c|)^2, \xi=\{R,G,B\} \tag{8} LtvA=N1i=1∑Nc∈ξ∑(∣(▽xAnc∣+∣▽yAnc∣)2,ξ={R,G,B}(8)
其中, N N N 为迭代次数, ▽ x \bigtriangledown_{x} ▽x, ▽ y \bigtriangledown_{y} ▽y 分别代表水平和垂直方向的梯度操作。
实验结果
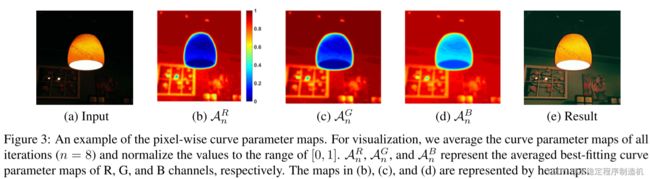
A n c \mathcal{A}_{n}^c Anc 可视化
不同loss对于结果的影响

L c o l L_{col} Lcol 的影响真的很大…
训练数据对于结果的影响
其他的一些可视化结果往往都比较常规,这里就不放了。论文中,作者还分析了训练数据的时候对于最终结果的影响,还比较有趣:

使用不同数据集对Zero-DCE进行训练:1)原训练集中(2422)的900张low-light图像Zero-DCELow ;2)DARK FACE中9000张未标注的low-light图像Zero-DCELargeL ;3)SICE数据集Part 1 and Part2组合的4800张多重曝光图像Zero-DCELargeLH
从(d)中可以看出,移除曝光数据后,Zero-DCE都会过度曝光那些well-lit区域(例如脸部);从(e)中可以看出,使用更多的多重曝光的训练数据,Zero-DCE对黑暗区域的恢复效果会更好。
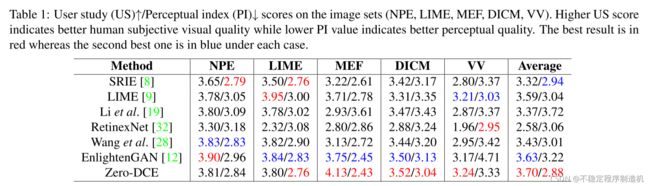
User Study & Application Study
总结
这篇paper质量很不错,是值得精读的。
优点:
- 作者从Curve Adjustment收到启发,用CNN去学习Curve而不是直接学习输出图像,不仅是一种新的思路,而且还能使得网络可以十分轻量;
- 首次在暗光增强领域引入了无监督学习,而且效果看起来相当不错;
- 文章作为一篇“卖方法”的文章,其行文写作十分顺畅,很值得学习。作者在Approach的写作中没有墨守常规,反而大胆地围绕本文核心贡献点——“LE-Curve”来展开全文,循序渐进引导读者,简明地表达出了LE-Curve的合理性。在Expriment部分的写作中,作者也将证明本文所提出方法的必要性(这里不是说LE-Curve的必要性,而是说为了学习出一个好的LE-Curve,本文所作出一系列设计的必要性)放在最重的位置,重说理、轻对比,牢牢的拴住了读者的注意力。
缺点:
如果非常吹毛求疵的话,个人觉得本文有一点没讲清楚:
- 无监督学习引入暗光增强领域的必要性没有体现出来。本文在开头简单提了一句,无监督学习能够提升算法的泛化性。但是我在后续的实验重并没有发现相关的佐证,可能是作者认为这点已经是共识了,不需要再加以突出了?但个人的观感,这无疑削弱了将”无监督学习首次引入暗光增强任务“这一个贡献点的重要性;
参考文献
因为我比较懒,本文大量的文字直接摘自第三方博客,特别感谢一下这位作者的付出。