CFT：Multi-Camera Calibration Free BEV Representation for 3D Object Detection——论文笔记

参考代码：暂无

1. 概述

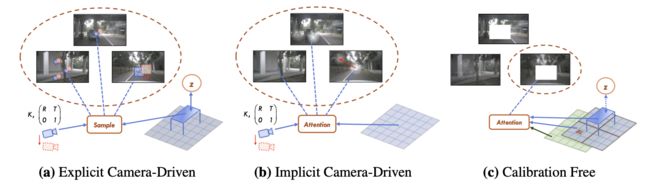
介绍：在相机数据作为输入的BEV感知算法中很多是需要显式或是隐式使用相机内外参数的，但是相机的参数自标定之后并不是一直保持不变的，这就对依赖相机标定参数的算法带来了麻烦。如何提升模型对相机参数鲁棒性，甚至是如何去掉相机参数成为一种趋势。对应的这篇文章完全去除了相机参数依赖，首先通过PA（position-aware enhancement）实现强大BEV空间位置编码，之后BEV空间位置编码与图像特征做cross attention实现BEV特征提取，这里的cross attention是针对特定区域的VA（view-aware attention），这个区域是通过相机空间布置位置作为先验进行划分的。这样通过上述的两个模块构建了一个高效的BEV空间特征提取网络，并且在内存占用和计算效率上有了较大提升。

对于相机参数的使用可以划分为如下几种使用方法：

• 1）显式使用：通过内外参数建立3D空间和2D空间中的对应关系，并以此对应关系进行特征索引或提取，带来的好处是直观并且收敛速度快，但对相机参数很敏感。
• 2）隐式使用：将内外参数隐式编码（embedding）并通过query的形式获取最后的特征表达，好处是对相机参数相对鲁棒。但是做query的维度不能太大（CVT的querysize为25），否则计算量和内存扛不住，太小也导致性能会被削减厉害。
• 3）完全不使用：这类方法中完全抛弃了相机参数，通过构建attention机制实现BEV特征和图像特征的关联，从而得到BEV表达。但是这需要强大的position/content表达和cross attention算力，实际训练和部署中也会存在对应的问题。但是文章通过提出的PA和view-aware attention给出了一个可行方案。

按照以上三种相机使用方法进行划分，文中对现有的一些方法进行划分：

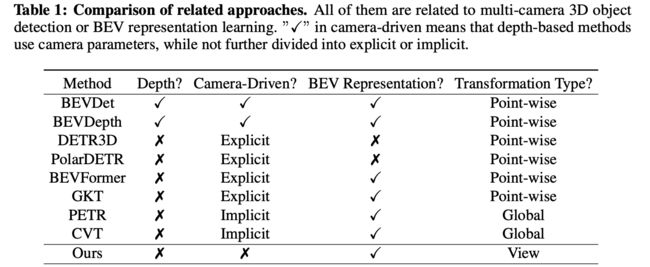
将文章的方法和其它一些方法对比相机参数鲁棒性：

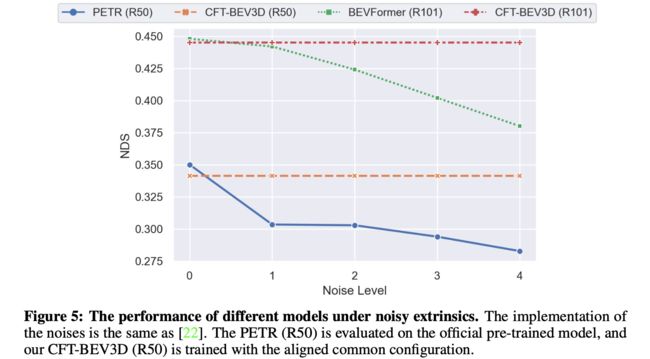
一条近乎直线的变化，稳得一批。

2. 方法设计

2.1 网络pipeline

文章的网络pipeline见下图所示：

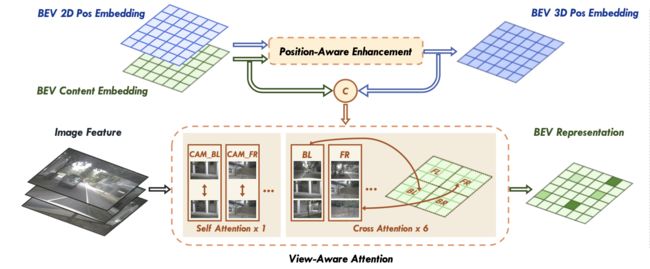
在上图中可以看到文章提出的两点改进PA和VA。其中PA是对位置编码进行强化，其使用了BEV 2D和content编码，并通过PA网络实现特征增强。

2.2 Position-aware Attention

PA的网络结构见下图所示：

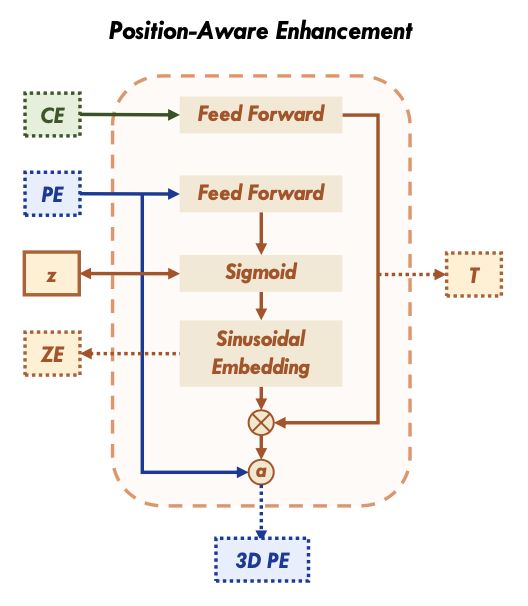
对于BEV的2D query表示为$Q_p\in R^{H_b\ast W_b\ast C_p}$，这个2Dquery会经过FFN网络和sigmoid激活之后用于表示BEV的高度信息：
$$z_{ref}=Norm(Sigmoid(FFN(Q_{ref})))$$
自然这个高度信息也是可以添加实际监督约束（如L1 loss）的，不过文中后续实验表明显式添加约束可不需要。之后再经过正弦函数编码与BEV 2D query做融合：
$$Q_{ep}=add(M\cdot Q_{ref},Q_p),M=FFN(Q_c),Q_{ref}=Sinuoidal(z_{ref})$$
其中，BEV content query $Q_c\in R^{H_b\ast W_b\ast C_s}$，最后整个BEV的query表示为$Q_c,Q_{ep}$concat的形式：
$$Q_{bev}=cat(Q_c,Q_{ep})$$
对于高度$z$是否添加显式约束，可以看下图中标注或学习的$z$和学习到位置编码之间的关系：

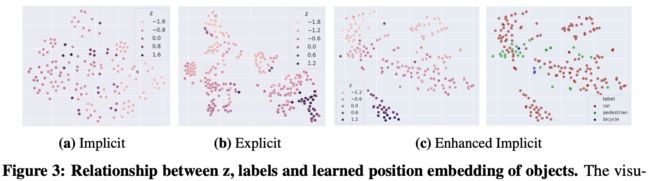
可以看到即使没有显式$z$约束，使用文章的位置编码也能获得与显式约束类似的聚类结果。下表也验证了文中的PA和PA中是否显式约束$z$带来的性能影响：

2.3 View-aware Attention

对于图像也会使用视图编码$P_v$、坐标位置编码$P_x,P_y$和原图像特征$F_s$一同组合得到：
$$P_{image}=cat(F_s,P_x,P_y,P_v)$$
将其reshape之后得到$P_{image}^{{}^{\prime }}\in R^{N_v\ast H_s{W}_s\ast C},C=C_s+C_p$，其会经过一个self-attention模块做特征增强。接下来便是文章减少计算量和内存消耗的步骤了，对$P_{bev}$划分为4个小网格，如上面pipeline中所示的那样，得到$P_{bev}^{{}^{\prime }}\in R^{N_v\ast \frac{H_b}{N_H}\frac{W_b}{N_W}\ast C},N_H=N_W=2,N_v=N_H\ast N_W$。同样对图像特征$P_{image}^{{}^{\prime }}$也进行进行分组得到$G\in R^{N_v\ast N_g{H}_s{W}_s\ast C}$，其分组的形式见下图所示：

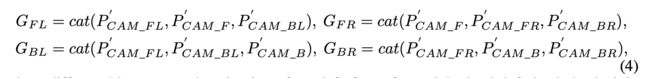
这样通过分组attention的形式避免global attention带来的巨大计算量，从而达到减少计算量的目的。除了上述提到的均匀分组之外，文章还实验了别的不同分组方式（如不同网格大小，极坐标划分等），其性能比较见下表：

3. 实验结果

nuScenes上的性能比较：