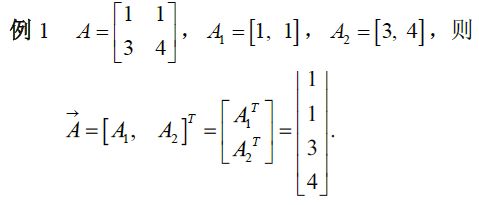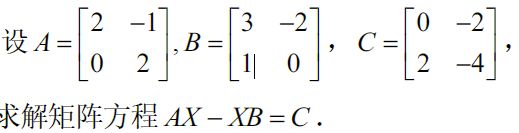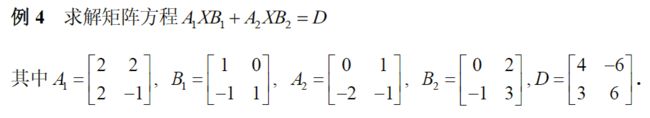【矩阵论】4. 矩阵运算——矩阵拉直
4.3 矩阵拉直
4.3.1 定义
按行拉直:按行分块:列向量
eg
4.3.2 拉直性质
线性性质:
- A + B → = A ⃗ + B ⃗ \overrightarrow{A+B}=\vec{A}+\vec{B} A+B=A+B
- k A → = k A ⃗ \overrightarrow{kA}=k\vec{A} kA=kA
X = X ( t ) ∈ C m × n X=X(t)\in C^{m\times n} X=X(t)∈Cm×n ,则 d X → d t = d d t X ⃗ \frac{\overrightarrow{dX}}{dt}=\frac{d}{dt}\vec{X} dtdX=dtdX
拉直三项公式
-
A B C → = ( A ⊗ C T ) B ⃗ \overrightarrow{ABC}=(A\otimes C^T)\vec{B} ABC=(A⊗CT)B
证明:
-
在方程组中为 A X B → = ( A ⊗ X T ) X ⃗ \overrightarrow{AXB}=(A\otimes X^T)\vec{X} AXB=(A⊗XT)X
乘积推广:两项拉直可以看做特殊三项拉直
设 A = ( a i j ) m × m , X = ( x i j ) m × n , B = ( b i j ) n × n A=(a_{ij})_{m\times m},X=(x_{ij})_{m\times n},B=(b_{ij})_{n\times n} A=(aij)m×m,X=(xij)m×n,B=(bij)n×n
A X → = A X I n → = ( A ⊗ I n ) X ⃗ X B → = I m X B → = ( I m ⊗ B T ) X ⃗ A X + X B → = ( A X I n → + I m X B → ) = ( A ⊗ I n + I m ⊗ B T ) X ⃗ \overrightarrow{AX}=\overrightarrow{AXI_n}=(A\otimes I_n)\vec{X}\\ \overrightarrow{XB}=\overrightarrow{I_mXB}=(I_m\otimes B^T)\vec{X}\\ \overrightarrow{AX+XB}=(\overrightarrow{AXI_n}+\overrightarrow{I_mXB})=(A\otimes I_n+I_m\otimes B^T)\vec{X} AX=AXIn=(A⊗In)XXB=ImXB=(Im⊗BT)XAX+XB=(AXIn+ImXB)=(A⊗In+Im⊗BT)X
4.3.3 应用——矩阵方程
前置知识:正规方程求解
拉直可求解线性矩阵方程 A X B = C AXB=C AXB=C ,其中 A = A m × n , X = X n × p , B = B p × q A=A_{m\times n},X=X_{n\times p},B=B_{p\times q} A=Am×n,X=Xn×p,B=Bp×q
记 X = ( x i j ) n × p X=(x_{ij})_{n\times p} X=(xij)n×p ,即为 n p np np 个未知量 x i j x_{ij} xij 的线性方程组
根据拉直公式,则方程 A X B = C AXB=C AXB=C 可被拉直为 ( A ⊗ B T ) X ⃗ = C ⃗ (A\otimes B^T)\vec{X}=\vec{C} (A⊗BT)X=C
推广:一般的线性矩阵方程 A 1 X B 1 + A 2 X B 2 + ⋯ + A S X B S = C A_1XB_1+A_2XB_2+\cdots+A_SXB_S=C A1XB1+A2XB2+⋯+ASXBS=C
A 1 X B 1 + A 2 X B 2 + ⋯ + A s X B s → = C ⃗ ⟺ ( A 1 ⊗ B 1 T + ⋯ + A s ⊗ B s T ) X ⃗ = C ⃗ \begin{aligned} \overrightarrow{A_1XB_1+A_2XB_2+\cdots+A_sXB_s}=\vec{C}\iff(A_1\otimes B_1^T+\cdots+A_s\otimes B_s^T)\vec{X}=\vec{C} \end{aligned} A1XB1+A2XB2+⋯+AsXBs=C⟺(A1⊗B1T+⋯+As⊗BsT)X=C
拉直前有解则拉直后也有解
- A X B = C AXB=C AXB=C 有解的充要条件为 r ( A ⊗ B T ∣ C ⃗ ) = r ( A ⊗ B T ) r(A\otimes B^T\mid\vec{C})=r(A\otimes B^T) r(A⊗BT∣C)=r(A⊗BT)
- 齐次方程 A X B = 0 AXB=0 AXB=0 的基础解系含有 n p − r ( A ⊗ B T ) = n p − r ( A ) r ( B ) np-r(A\otimes B^T)=np-r(A)r(B) np−r(A⊗BT)=np−r(A)r(B)
a. 有解与唯一解条件
b. 里亚普诺夫矩阵方程
A X + X B = C AX+XB=C AX+XB=C ,其中 A ∈ C m × m . B ∈ C n × n , X ∈ C m × n A\in C^{m\times m}.B\in C^{n\times n},X\in C^{m\times n} A∈Cm×m.B∈Cn×n,X∈Cm×n
-
使用拉直公式
A X + X B = C ⟺ ( A X I n → + I m X B → ) = ( A ⊗ I n + I m ⊗ B T ) X ⃗ = C ⃗ AX+XB=C\iff (\overrightarrow{AXI_n}+\overrightarrow{I_mXB})=(A\otimes I_n+I_m\otimes B^T)\vec{X}=\vec{C} AX+XB=C⟺(AXIn+ImXB)=(A⊗In+Im⊗BT)X=C
-
有解的充要条件为 r ( A ⊗ I n + I m ⊗ B T ∣ C ⃗ ) = r ( A ⊗ I n + I m ⊗ B T ) r(A\otimes I_n+I_m\otimes B^T\mid\vec{C})=r(A\otimes I_n+I_m\otimes B^T) r(A⊗In+Im⊗BT∣C)=r(A⊗In+Im⊗BT)
-
唯一解充要条件 : ∣ A ⊗ I n + I m ⊗ B T ∣ ≠ 0 \vert A\otimes I_n+I_m\otimes B^T\vert\neq 0 ∣A⊗In+Im⊗BT∣=0
根据特征值计算 ∣ A ⊗ I n + I m ⊗ B T ∣ \vert A\otimes I_n+I_m\otimes B^T\vert ∣A⊗In+Im⊗BT∣
定理1:
- A X + X B = C AX+XB=C AX+XB=C 有唯一解 ⟺ A ⊗ I n + I m ⊗ B T \iff A\otimes I_n+ I_m\otimes B^T ⟺A⊗In+Im⊗BT 可逆 ⟺ A \iff A ⟺A 和 ( − B ) (-B) (−B) 无公共特根
- A X − X B = C AX-XB=C AX−XB=C 有唯一解 ⟺ A ⊗ I n − I m ⊗ B T \iff A\otimes I_n- I_m\otimes B^T ⟺A⊗In−Im⊗BT 可逆 ⟺ A \iff A ⟺A 和 B B B 无公共特根
若 A = A m × m A=A_{m\times m} A=Am×m 的特根为 λ 1 , λ 2 , ⋯ , λ m \lambda_1,\lambda_2,\cdots,\lambda_m λ1,λ2,⋯,λm , B = B n × n B=B_{n\times n} B=Bn×n 的特根为 t 1 , t 2 , ⋯ , t n t_1,t_2,\cdots,t_n t1,t2,⋯,tn ,则 A ⊗ I n + I m ⊗ B T A\otimes I_n+I_m\otimes B^T A⊗In+Im⊗BT 的 m n mn mn 个特根为 { λ k + t j } \{\lambda_k+t_j\} {λk+tj} ; A ⊗ I n − I m ⊗ B T A\otimes I_n-I_m\otimes B^T A⊗In−Im⊗BT 的 mn 个特征值 { λ k − t j } \{\lambda_k-t_j\} {λk−tj} ( k = 1 , 2 , ⋯ , m , j = 1 , 2 , ⋯ , n ) (k=1,2,\cdots,m,j=1,2,\cdots,n) (k=1,2,⋯,m,j=1,2,⋯,n)
因为 B B B 与 B T B^T BT 有相同的特征值
⇒ \Rightarrow ⇒ ∣ A ⊗ I n ± I m ⊗ B T ∣ \vert A\otimes I_n\pm I_m\otimes B^T\vert ∣A⊗In±Im⊗BT∣ 的 m n mn mn 个特征值为 $ (\lambda_k\pm t_j)$
⇒ A ⊗ I n ± I m ⊗ B \Rightarrow A\otimes I_n\pm I_m\otimes B ⇒A⊗In±Im⊗B 不可逆的条件为 无零根 即 { λ k ± t j ≠ 0 } \{\lambda_k\pm t_j\neq 0\} {λk±tj=0}
⟺ A \iff A ⟺A 与 ( ± B ) (\pm B) (±B) 没有公共特征值
定理2: 若 A 和 B 的特根都有负实部,则 A X + X B = C AX+XB=C AX+XB=C 有唯一解
- 若特根都在左半平面,则 A A A 与 − B -B −B 不会有公共特根
定理3 :若 A 和 B 分别为m阶和n阶方阵,若A和B没有公共特征值,则 [ A C 0 B ] \left[\begin{matrix}A&C\\0&B\end{matrix}\right] [A0CB] 与 [ A 0 0 B ] \left[\begin{matrix}A&0\\0&B\end{matrix}\right] [A00B] 相似
定理4 :若 A ∈ C m × m , B ∈ C n × n , F ∈ C m × n A \in C^{m\times m},B\in C^{n\times n},F\in C^{m\times n} A∈Cm×m,B∈Cn×n,F∈Cm×n ,若A和B没有公共特根,则 [ A C F B ] \left[\begin{matrix}A&C\\F&B\end{matrix}\right] [AFCB] 与 [ A C 0 B ] \left[\begin{matrix}A&C\\0&B\end{matrix}\right] [A0CB] 相似
- 证明:令 P = ( I 0 X I ) , P − 1 = ( I 0 − X I ) P=\left(\begin{matrix}I&0\\X&I\end{matrix}\right),P^{-1}=\left(\begin{matrix}I&0\\-X&I\end{matrix}\right) P=(IX0I),P−1=(I−X0I) ,则有许尔公式, P ( A 0 F B ) P − 1 = ( A 0 X A − B X + F B ) P\left(\begin{matrix}A&0\\F&B\end{matrix}\right)P^{-1}=\left(\begin{matrix}A&0\\XA-BX+F&B\end{matrix}\right) P(AF0B)P−1=(AXA−BX+F0B) ,若为对角阵,则 A X − B X = − F ⇒ A X − B X = F AX-BX=-F\Rightarrow AX-BX=F AX−BX=−F⇒AX−BX=F
eg
1. 求解矩阵方程
A的特征值为 -2,3;B的特征值为1,1。矩阵方程拉直为 A X + X B = C ⟺ ( A ⊗ I 2 + I 2 ⊗ B T ) X ⃗ = C ⃗ AX+XB=C\iff(A\otimes I_2+I_2\otimes B^T)\vec{X}=\vec{C} AX+XB=C⟺(A⊗I2+I2⊗BT)X=C 。而A与-B没有公共特征值,则拉直后方程具有唯一解。
λ ( A ) = { 2 , 2 } , λ ( B ) = { 1 , 2 } \lambda(A)=\{2,2\},\lambda(B)=\{1,2\} λ(A)={2,2},λ(B)={1,2} ,故A和B有公共特征值,故解不唯一,
A X − X B = C AX-XB=C AX−XB=C 可拉直为 ( A ⊗ I 2 × 2 − I 2 × 2 ⊗ B T ) X ⃗ = C ⃗ (A\otimes I_{2\times 2}-I_{2\times 2}\otimes B^T)\vec{X}=\vec{C} (A⊗I2×2−I2×2⊗BT)X=C ,有 X = [ x 1 x 2 x 3 x 4 ] , X ⃗ = ( x 1 x 2 x 3 x 4 ) X=\left[\begin{matrix}x_1&x_2\\x_3&x_4\end{matrix}\right],\vec{X}=\left(\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right) X=[x1x3x2x4],X=⎝⎜⎜⎛x1x2x3x4⎠⎟⎟⎞
( A ⊗ I 2 × 2 − I 2 × 2 ⊗ B T ) X ⃗ = ( − 1 − 1 − 1 0 2 2 0 − 1 0 0 − 1 − 1 0 0 2 2 ) ( x 1 x 2 x 3 x 4 ) = ( 0 − 2 2 − 4 ) ⟺ G X = b (A\otimes I_{2\times 2}-I_{2\times 2}\otimes B^T)\vec{X}=\left(\begin{matrix}-1&-1&-1&0\\2&2&0&-1\\0&0&-1&-1\\0&0&2&2\end{matrix}\right)\left(\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right)=\left(\begin{matrix}0\\-2\\2\\-4\end{matrix}\right) \iff GX=b (A⊗I2×2−I2×2⊗BT)X=⎝⎜⎜⎛−1200−1200−10−120−1−12⎠⎟⎟⎞⎝⎜⎜⎛x1x2x3x4⎠⎟⎟⎞=⎝⎜⎜⎛0−22−4⎠⎟⎟⎞⟺GX=b 由于 r ( G ∣ b ) = r ( G ) = 3 r(G\vert b)=r(G)=3 r(G∣b)=r(G)=3 ,故方程有解,其解为 ( G ∣ b ) → ( 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 − 4 4 − 6 0 ) (G\vert b)\rightarrow \left(\begin{array}{c:c} \begin{matrix} 1&1&0&0\\ 0&0&1&0\\0&0&0&1\\0&0&0&0 \end{matrix}& \begin{matrix} -4\\ 4\\-6\\0 \end{matrix} \end{array}\right) (G∣b)→⎝⎜⎜⎛1000100001000010−44−60⎠⎟⎟⎞
故 G 的解为 X = ( − 4 0 4 6 ) + t ( 1 − 1 0 0 ) X=\left(\begin{matrix}-4\\0\\4\\6\end{matrix}\right)+t\left(\begin{matrix}1\\-1\\0\\0\end{matrix}\right) X=⎝⎜⎜⎛−4046⎠⎟⎟⎞+t⎝⎜⎜⎛1−100⎠⎟⎟⎞ 原矩阵方程的解为 X = ( − 4 0 4 6 ) + t ( 1 − 1 0 0 ) X=\left(\begin{matrix}-4&0\\4&6 \end{matrix}\right)+t\left(\begin{matrix}1&-1\\0&0\end{matrix}\right) X=(−4406)+t(10−10)
2. 求解一般的矩阵方程 A 1 X B 1 + ⋯ + A s X B s = C A_1XB_1+\cdots+A_sXB_s=C A1XB1+⋯+AsXBs=C
3. 求解 A X − X A = μ X AX-XA=\mu X AX−XA=μX
-
将方程拉直为 ( A ⊗ I n − I n ⊗ A T ) X ⃗ = μ X ⃗ (A\otimes I_n-I_n\otimes A^T)\vec{X}=\mu \vec{X} (A⊗In−In⊗AT)X=μX
-
记 G = A ⊗ I n − I n ⊗ A T G=A\otimes I_n-I_n\otimes A^T G=A⊗In−In⊗AT 原方程化为 G X ⃗ = μ X ⃗ ⇒ ( G − μ I ) X ⃗ = 0 G\vec{X}=\mu \vec{X}\Rightarrow (G-\mu I)\vec{X}=0 GX=μX⇒(G−μI)X=0
有非零解条件为 ∣ G − μ I ∣ = 0 \vert G-\mu I\vert=0 ∣G−μI∣=0 ,即 μ \mu μ 是 G的特征值,而 λ ( G ) = { λ r − λ s } \lambda(G)=\{\lambda_r-\lambda_s\} λ(G)={λr−λs}
故 有非零解条件为: ∃ r , s \exist r,s ∃r,s ,使 μ = λ r − λ s , 1 ≤ r , s ≤ n \mu=\lambda_r-\lambda_s,1\le r,s\le n μ=λr−λs,1≤r,s≤n
λ ( A ) = { 1 , 3 } \lambda(A)=\{1,3\} λ(A)={1,3}, G = A ⊗ I 2 − I 2 ⊗ A T = ( 0 − 2 0 0 0 − 2 0 0 2 0 2 − 2 0 2 0 0 ) G=A\otimes I_2-I_2\otimes A^T=\left(\begin{matrix}0&-2&0&0\\0&-2&0&0\\2&0&2&-2\\0&2&0&0\end{matrix}\right) G=A⊗I2−I2⊗AT=⎝⎜⎜⎛0020−2−202002000−20⎠⎟⎟⎞ λ ( G ) = { λ ( A ) i − λ ( A ) j } = { 2 , 0 , 0 , − 2 } \lambda(G)=\{\lambda(A)_i-\lambda(A)_j\}=\{2,0,0,-2\} λ(G)={λ(A)i−λ(A)j}={2,0,0,−2} ,故 ∃ λ ( G ) = μ = − 2 \exist \lambda(G)=\mu=-2 ∃λ(G)=μ=−2 ,矩阵方程有非零解
X = ( x 1 x 2 x 3 x 4 ) X=\left(\begin{matrix}x_1&x_2\\x_3&x_4\end{matrix}\right) X=(x1x3x2x4) , X ⃗ = ( x 1 x 2 x 3 x 4 ) \vec{X}=\left(\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right) X=⎝⎜⎜⎛x1x2x3x4⎠⎟⎟⎞ ,解 G X ⃗ = 0 G\vec{X}=0 GX=0 ⇒ X ⃗ = t 1 ( − 1 0 ) + t 2 ( 1 0 ) = ( − t 1 t 2 0 0 ) \Rightarrow \vec{X}=t_1\left(\begin{matrix}-1\\0\end{matrix}\right)+t_2\left(\begin{matrix}1\\0\end{matrix}\right)=\left(\begin{matrix}-t_1&t_2\\0&0\end{matrix}\right) ⇒X=t1(−10)+t2(10)=(−t10t20) ,故原矩阵方程的解 X = ( − t 1 t 2 0 0 ) X=\left(\begin{matrix}-t_1\\t_2\\0\\0\end{matrix}\right) X=⎝⎜⎜⎛−t1t200⎠⎟⎟⎞
由拉直公式 d X d t = A X + X B = ( A ⊗ I n + I m ⊗ B T ) X ⃗ = C ⃗ \frac{dX}{dt}=AX+XB=(A\otimes I_n+I_m\otimes B^T)\vec{X}=\vec{C} dtdX=AX+XB=(A⊗In+Im⊗BT)X=C
X ⃗ = e t ( A ⊗ I n + I m ⊗ B T ) D ⃗ = e t ( A ⊗ I n ) e t ( I m ⊗ B T ) D ⃗ = = ( e t A ⊗ I n ) ( I m ⊗ e t B T ) D ⃗ = ( e t A I m ⊗ I n e t B T ) D ⃗ = ( e t A ⊗ e t B T ) D ⃗ = e t A D ( ( e t B T ) ) T → = . . . \begin{aligned} &\vec{X}=e^{t(A\otimes I_n+I_m\otimes B^T)}\vec{D}=e^{t(A\otimes I_n)}e^{t(I_m\otimes B^T)}\vec{D}==(e^{tA}\otimes I_n)(I_m\otimes e^{tB^T})\vec{D}\\ &=(e^{tA}I_m\otimes I_ne^{tB^T})\vec{D}=(e^{tA}\otimes e^{tB^T})\vec{D }=\overrightarrow{e^{tA}D((e^{tB^T}))^T}=... \end{aligned} X=et(A⊗In+Im⊗BT)D=et(A⊗In)et(Im⊗BT)D==(etA⊗In)(Im⊗etBT)D=(etAIm⊗InetBT)D=(etA⊗etBT)D=etAD((etBT))T=...