【大数据分析与挖掘】决策树（ID３、Ｃ４.５、CART）与随机森林、集成学习学习笔记，Boosting与Bagging

一.决策树与随机森林

1.决策树

一种类似于流程图的树结构，属于经典的十大数据挖掘算法之一，其规则就是IF…THEN…(IF…ELSE…)的思想，可用于数值型因变量的预测和离散型因变量的分类，是一种有监督学习模型，常被用于分类问题和回归问题。

决策树是一类机器学习算法，他们的共同点都是采用了树形结构，基本原理都是用一长串的if-else(节点划分)完成样本分类，区别主要在纯度度量(节点字段选择指标)等细节上选择了不同的解决方案。

该算法简单直观、通俗易懂，不需要研究者掌握任何邻域的知识或复杂的数学推理，而且算法的结果输出具有很强的解释性。

信息熵是度量样本集合“纯度”最常用的一种指标。计算公式如下：

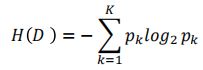
假定当前样本集合D中第k类样本所占的比列为p_k（k=1,2,…,K)

整个决策树建立的关键是：节点字段的选择指标（分裂准则），也是算法的核心。
以下介绍三种经典的决策树算法：

①ID3

节点字段的选择指标是信息增益，实现根节点或中间节点的字段选择。

Gain_A(D)表示用特征A对样本集合D进行划分所获得的信息增益，H(D)表示D的信息熵，H(D|A)表示D在A条件下的条件熵。信息增益表示在A的条件下，信息“不确定性”减少的程度。

一般而言，信息增益越大，则意味着使用特征A对集合D进行划分后所获得的“纯度提升”越大。但该指标存在一个非常明显的缺点，即信息增益会偏向于取值较多的字段。

ID3选择信息增益最大的特征作为决策树根节点的判断。

②C4.5

节点字段的选择指标是信息增益率，实现根节点或中间节点的字段选择。

为了克服信息增益指标的缺点，提出了信息增益率的概念，它的思想很简单，就是在信息增益的基础上进行相应的惩罚。

H_A(D)为数据集D关于特征A的信息熵。特征A的取值越多，特征A的信息增益Gain_A(D)可能越大，但同时H_A(D)也会越大，这样以商的形式就实现了Gain_A(D)的惩罚。

C4.5选择信息增益率最大的特征作为决策树根节点的判断。

③CART

节点字段的选择指标是基尼指数

为了能够让决策树预测连续型的因变量，提出CART算法，该算法也称为分类回归树。

Gini(D)反映的是数据集D的不确定性，跟信息熵 的含义类似。因此Gini(D)越小，则数据集D的“纯度”越高。
特征A的基尼指数为：

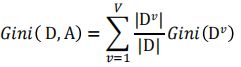
Gini(D,A)反映的是使用特征A对数据集合D进行划分后的不确定程度。
CART选择基尼指数最小的特征作为决策树根节点的判断。

区别

1.决策树CART算法既可以处理离散型变量的分类问题，也可以解决连续型变量的回归预测问题。但C4.5和ID3算法都只能用于离散型变量的分类问题。
2.ID3和C4.5都属于多分支决策树，即每次分叉生成子树时，都是按照所选特征的所有取值来划分的。CART则是二分支决策树。
3.三种算法在建模过程中都可能存在过拟合的情况。

过拟合和剪枝处理

所谓过拟合，即模型在训练集上有很高的预测精度，但在测试集上效果却不够理想。
欠拟合情况是没有很好地捕捉到数据的特征，不能很好地拟合数据。
过拟合情况是模型过于复杂，把噪声数据的特征也学习到模型中。

为了解决过拟合问题，通常会对决策树做剪枝处理。
决策树的剪枝通常有两类方法：
一类是预剪枝，指在树的生长过程中就对其进行必要的剪枝；
一类是后剪枝，指决策树在得到充分生长的前提下再对其返工修剪。
后剪枝方法有误差降低剪枝法、悲观剪枝法和代价复杂度剪枝法。

2.集成学习

集成分类器是一个复合模型，由多个分类器组合而成。
提升(Boosting)、装袋(Bagging)都是流行的集成学习方法。

①提升(Boosting)

该方法训练基分类器时采用串行的方式，各个基分类器之间有依赖。

主要思想：从错误中学习。即每层训练时，对前一层基分类器分错的样本，给予更高的权重，测试时，根据各层分类器的结果的加权得到最终结果。

通过逐步聚焦于基分类器分错的样本，减少集成分类器的偏差。

Adaboost

是一种流行的自适应提升算法，也是一种迭代算法，是Boosting的典型代表。

核心思想是针对同一个训练集训练不同的分类器(弱分类器)，然后把这些弱分类器集合起来，构成一个更强的最终分类器(强分类器)。

②袋装(Bagging)

该方法与Boosting的串行训练方式不同，Bagging方法在训练过程中，各基分类器之间无强依赖，可以并行训练。

主要思想：集体投票决策，每个个体单独作出判断，再通过投票的方式做出最后的集体决策。

采取分而治之的策略，通过对训练样本多次采样，并分别训练出多个不同模型，然后做综合，以减小集成分类器的方差。

随机森林(Random Forest)

该算法是Bagging的典型代表。

为了让基分类器之间相互独立，将训练集分为若干子集，当训练样本数量较少时，子集之间可能有交叠。

“森林”：由多棵决策树构成的集合，而且这些子树都是经过充分生长的CART树
“随机”：构成多棵决策树的数据是随机生成的，生成过程采用的是Bootstrap抽样法，即有放回地随机抽取样本。
Bagging是Bootstrap Aggregating的简称，意思是再抽样，然后在每个样本上训练出来的模型取平均。

核心思想：采用多棵决策树的投票机制，完成分类或预测问题的解决。
对于分类问题，将多棵树的判断结果用作投票，根据少数服从多数的原则，最终确定样本所属的类型；对于预测性问题，将多棵树的回归结果进行平均，最终用于样本的预测值。

优点：运行速度快，预测准确率高

随机森林的随机性体现在两个方面：
一是每棵树的训练样本是随机的：
“样本随机性”在于从N个样本中有放回地随机抽取N个样本作为一棵子树的训练集（有些样本可能是重复的，有些样本则可能没被抽到）。
二是树中每个节点的分裂字段也是随机选择的：
“特征随机性”在于从M个特征中不放回地随机抽取m个，m的取值一般为m=√M。
两个随机性的引入，再加上最终的投票机制（分类；多数表决）或取平均值（回归），随机森林不剪枝也不容易陷入过拟合。

Boosting和Bagging的基分类器（弱分类器）都为CART。