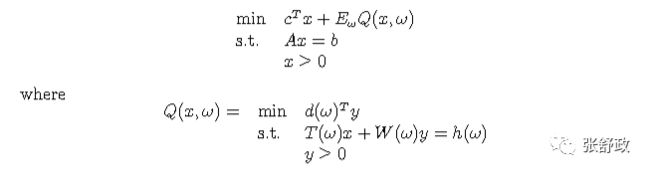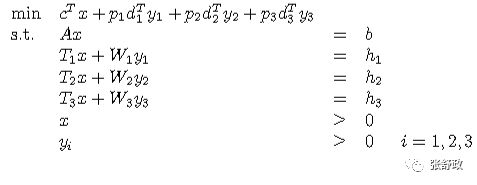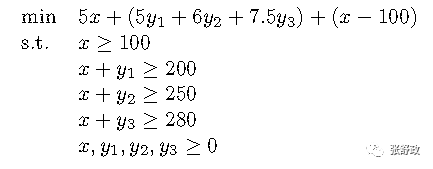随机规划及其Recourse(追索/补偿)问题
最近在读有关随机规划论文时遇到了一个Recourse,译作“追索”或“补偿”,但是没有人讲解Recourse问题到底是什么是什么,甚至搜索“Recourse”会出现“Resource”的内容。这篇文章谈谈随机规划(Stochastic Programming)和对应的追索(Recourse)问题。
本文主要参考了“https://neos-guide.org/content/stochastic-linear-programming”。另外本文举的例子非常浅显,想了解更符合现实的模型可以参考“https://blog.csdn.net/weixin_43964257/article/details/116492778”。
介绍
Recourse这个词来源于法律,也就是我们常说的"追索权",关于这个概念百度百科解释如下:
“追索权,是指持票人在汇票到期未获付款,到期前未获承兑或其他法定原因发生时,在采取保全权利行为之后,能够请求前手或其他票据债务人偿还票据金额以及相关损失的票据权利,是法律上为补充付款请求权而设定的第二次请求权。”
一句话总结,当甲拥有债权时当事人乙拒绝付款,甲可以依照法律要求乙补充付款。笔者法律知识有限,有误解之处请大家指正,但只需理解Recourse指“要求补齐欠款的权利”。
Recourse是随机规划中的核心概念,指的是在随机事件发生后采取修正的能力。一个简单的二阶段Recourse例子如下:
-
选择决策变量Xi来控制今天发生的事;
-
夜里,发生了随机事件;
-
第二天,采取行动yi来修正随机事件带来的不确定性。
随机规划分为两个阶段,分别为“here and now” 和 “wait and see”,第二个阶段即为Recourse阶段。
例子
假如你是一个煤老板,在购置煤炭时,一部分在当年售卖给客户,另一部分可以存储起来来年售卖。售卖煤炭时,也可以选择购置还是调用库存。
因此你的决策为:
-
购置多少煤炭直接售卖给客户
-
购置多少煤炭用以存储
-
当年从库存中调用多少煤炭
你的决策主要基于现在和未来的煤炭售价,库存成本,库存容量,每阶段需求。
每个阶段的决策可以被构建为简单的线性规划(Linear Programming)问题,目标为最小化当年的成本。假如未来状况可以预料,则数据集确定,我们可以直接得到一个可行最优解。
但大多数情况下,我们并不知道未来的价格需求,但是我们可以进行预测。例如,如果客户购买煤炭主要为了取暖,则其需求量高度依赖于气候状况,只需预测天气就可以精准预测来年需求。
但不考虑不确定性会使我们的模型面临失效风险,我们的“最优决策”在现实中可能并不适用。
不同情况
假如,今年是个暖冬,明年冬天可能有三种情况:暖冬、冷冬、极寒,各个情况下系统参数如下:
| 气候 | 概率 | 煤价 | 需求 |
| 暖冬 |
1/3 | 5 |
100 |
| 冷冬 | 1/3 | 6 | 150 |
| 极寒 | 1/3 | 7.5 | 180 |
存储煤炭的消耗为每单位每年1元,如果我们将三种场景分情况讨论,则我们有三种最优的购买-存储策略。
暖冬-暖冬
| 年号 | 购买量 | 存储量 | 当前库存 | 总成本 |
| 1 | 100 | 0 | 0 | 500 |
| 2 | 100 | 0 | 0 | 500 |
暖冬-冷冬
| 年号 | 购买量 | 存储量 | 当前库存 | 总成本 |
| 1 | 100 | 0 | 0 | 500 |
| 2 | 150 | 0 | 0 | 900 |
暖冬-极寒
| 年号 | 购买量 | 存储量 | 当前库存 | 总成本 |
| 1 | 100 | 180 | 180 | 1580 |
| 2 | 0 | 0 | 0 | 0 |
我们不知道来年的气候,但我们想让今年的购买可以最小化期望成本。请记住,当做出第二次决策时,我们已经知道发生了哪种情况。
随机线性规划的数学模型
随机规划的数学表示如下,目标函数为最小化“第一阶段消耗+期望的第二阶段追索消耗”
一阶段线性规划的目标为最小化直接成本CTX加期望追索成本Q(X,ω),ω包含了符合AX=b时的所有场景。
此时,追索消耗Q取决于①一阶段决策X,②二阶段时间ω
第二个线性规划的目标为选择合适的y,以最小化消耗,Tx+Wy=h这个约束可以看作:随机事件发生后采取行动来修正系统。在文中实例中,这个约束代表着购买足够的煤炭来满足第二年的市场需求。
重要的一点是一阶段决策变量X与二阶段发生的事件是完全独立的,这被称为不可预料属性(Nonanticipativity Property),即我们不可以预知未来。
等效确定性模型(Deterministic Equivalent)
上述数学模型与我们平时见到的其他线性模型形式不同,但我们可以通过将y分情况讨论,把模型变为确定性模型,这叫做deterministic equivalent,我此处译为等效确定性模型。如下
上述为泛用性一般模型,具体到本文实例可以表示如下:
在当前模型中,仅有一个一阶段决策取值X,与3个场景对应有3个二阶段决策y1、y2、y3。一阶段决策变量必须在所有场景下均可行,因为我们考虑了所有场景,所以此处X为不确定条件下所有场景下的最优解。
每个场景下都有不同的T和W,所以模型维度与二阶段场景数量直接相关。由于约束形式类似,所以求解算法可以适用于所有情况。考虑不确定性会得到更具有鲁棒性(Rubust)的解,同时需要更多计算资源。
数学期望解
由于随机规划模型计算量更大,人们可能选择更简单的策略,在实例这种概率已知的条件下,我们尝试使用数学期望来求解。
此时的第二年期望需求为(100+150+180)/3=143.33,即我们第一年应购买243.33单位煤炭,第一年成本为243.33*5=1360,则三种情况下第二年消耗分别如下:
| 气候 | 购买/存储 情况 | 消耗 | 总成本 |
| 暖冬 | 剩余库存43.33 | 43.33*1=43.33 | 1403.33 |
| 冷冬 | 还需购买6.67 | 66.7*6=40 | 1400 |
| 极寒 | 还需购买33.67 | 33.67*7.5=275 | 1635 |
则总的期望成本为(1403.33+1400+1635)/3=1479.44
随机规划解
随机规划下本实例数学模型如下:
其中x为第一阶段的购置量,y1、y2、y3分别为三种不同情况下第二阶段的行动,约束条件非常简单易懂。
上述模型可以直接用单纯形法求解,无耐笔者运筹学知识遗忘严重,将模型在cplex中求解可得最优解为[x, y1, y2, y3] = [200, 0, 50, 80]。此时注意,与数学期望的单一解不同,我们同时求得了第一阶段的最优解和3个第二阶段最优解,即第二年会根据气候状况在y1, y2, y3中选取一解来执行,此时总成本如下表所示:
| 年份-气候 | 购置售卖 | 购置存储 | 库存量 | 总消耗 |
| 1-暖冬 | 100 | 100 | 100 | 1100 |
| 2-暖冬 | 0 | 0 | 0 | 0 |
| 2-冷冬 | 50 | 0 | 0 | 300 |
| 2-极寒 | 80 | 0 | 0 | 600 |
此时所有情况下的成本为1100+(0+300+600)/3=1400,比数学期望解下的成本下降了79.44。同时我们会发现,在所有情况下随机规划解都要比数学期望法解更优。例如在暖冬-极寒中,数学期望成本为1635,随即规划成本为1600。
结论
最后,回溯文中所有标红的文字,我们可以抓住随机规划及追索的核心概念:我们同时得到了所有情况下的解,代表了不同随机事件发生的情况下我们需要采取的行动。至此,追索(Recourse)的概念终于清晰,即随机规划需要求解的第二阶段决策变量。