【动手学深度学习】权重衰减(深度学习中的正则化)
原理:通过限制参数值的选择范围来控制模型容量
正则化:对学习算法的修改——旨在减少泛化误差而不是训练误差
权重衰减也叫做L2正则化
也就是说,如果想控制模型复杂度,比如不想让模型太复杂的话,可以通过增加拉姆达来满足需求
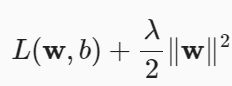
实例演示权重衰减:
从零开始实现
导入模块
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
n_train,n_test,num_inputs,batch_size = 20,100,200,5
true_w,true_b = torch.ones((num_inputs,1))*0.01,0.05
# d2l.synthetic_data:用来生成y=wx+b的训练数据
train_data = d2l.synthetic_data(true_w, true_b, n_train)
# 构造一个Pytorch的训练数据迭代器
train_iter = d2l.load_array(train_data, batch_size)
# d2l.synthetic_data:用来生成y=wx+b的测试数据
test_data = d2l.synthetic_data(true_w, true_b, n_test)
# 构造一个Pytorch的测试数据迭代器
test_iter = d2l.load_array(test_data, batch_size, is_train=False)
# 随机初始化模型参数
def init_params():
w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
# 定义L2范数惩罚
def l2_penalty(w):
return torch.sum(w.pow(2)) / 2
# 定义训练代码实现
def train(lambd):
# 随机初始化模型参数
w, b = init_params()
# lambda:匿名函数 net为线性网络 loss为平方差损失
net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
num_epochs, lr = 100, 0.003
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
# 增加了L2范数惩罚项,
# 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
l = loss(net(X), y) + lambd * l2_penalty(w)
l.sum().backward()
d2l.sgd([w, b], lr, batch_size)
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数是:', torch.norm(w).item())
# 忽略正则化直接训练
# 用lambd=0禁用权重衰减后运行这个代码
# 训练误差有了减少但是测试误差没有减少,说明出现了严重得过拟合
train(lambd=0)
# 使用权重衰减
# 在这里训练误差增大,但测试误差减少,这正是我们期望从正则化中得到得效果
train(lambd=3)
简洁实现
# 简洁实现
# 由于权重衰减在神经网络优化中很常见深度学习框架为了便于我们使用权重衰减,
# 将权重衰减集成到优化算法中,以便与任何损失函数结合使用。此外,这种集成还有计算上的好处
# 允许在不增加任何额外得计算开销的情况下向算法中添加权重衰减。由于更新的权重衰减
# 部分仅依赖于每个参数的当前值,因此优化器必须至少接触每个参数一次。
def train_concise(wd):
net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss(reduction='none')
num_epochs, lr = 100, 0.003
# 偏置参数没有衰减
trainer = torch.optim.SGD([
{"params":net[0].weight,'weight_decay': wd},
{"params":net[0].bias}], lr=lr)
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.mean().backward()
trainer.step()
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1,
(d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数:', net[0].weight.norm().item())
train_concise(0)
train_concise(3)
