3D点云配准算法-4PCS（4点全等集配准算法）

简介

4PCS算法是一种快速的、鲁棒的三维点云配准方案，该方案使用宽基底，对噪声和异常值具有良好的适应性，该算法允许对有噪声的原始数据进行配准，而无需对数据进行预过滤或去噪。此外，该方法大大减少了在噪声存在的情况下在潜在表面的可靠配准之间所需的试验次数，也无需对开始对准进行任何假设。我们的方法是基于一种新的技术，即我们从一个三点集（3D point set）中提取出的共面四点集（4-points sets）对于给点的另一个四点集在刚性变换下近似全等（后文细说，不懂没关系）。这个提取过程大致时间复杂度为O(n^2 + k)时间，其中n为候选点的数量，k为申明的4点集的数量（k也是计算得到的），在实际应用中，当噪声水平较低且有足够的重叠时，利用局部描述子将时间复杂度降低到O(n + k),我们还提出了一种处理相似性和仿射变换的扩展。与常见的随机配准技术相比，我们的技术实现了一个数量级的渐近加速。我们证明了我们的算法的鲁棒性通过多趟扫描每趟受不同程度的噪声，异常值，和重叠程度的影响。

近似全等四点集怎么定义？

利用刚性变换后交点所占线段比例不变以及点之间的欧几里得距离不变的特性，在目标点云中尽可能寻找４个近似共面点（近似全等四点集）与之对应，从而利用最小二乘法计算得到变换矩阵，基于RANSAC算法框架迭代选取多组基，根据最大公共点集（LCP）的评价准则进行比较得到最优变换。

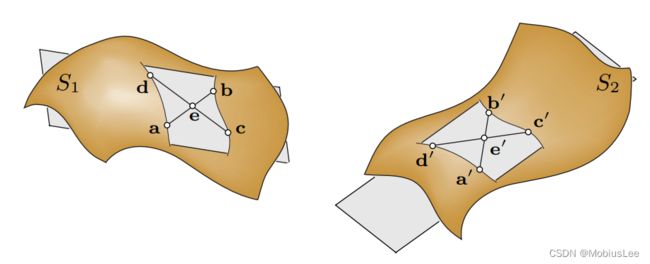
上图阐释了对于全等4点集的仿射不变比性质。给定表面S1上的点，设点a, b, c, d共面，直线ab和cd相交于点e。在任意的仿射变换下，保持比值 r1 = lla - ell / lla - bll 和比值 r2 = llc- ell / Ilc - dll 不变。如果S2是另一个与S1(部分)匹配的曲面，且4点共面基底位于重叠区域内，则S2对应的点集也是共面的，且满足以下关系: lla' - e'll / lla' - b'll= r1，llc' - e'll / Ilc' - d'll = r2。 

怎样生成我们需要的四点集？

step1：首先在源点云中随机选择三个点，要求这三点所构成的三角形面积尽量的大（三点确定一个平面，向量叉积可以计算面积），但是三点间的距离不能超过一定的阈值上限，该上限由两片点云的给定重叠率 f 确定。因为三点之间距离越大，配准的鲁棒性越高；但距离过大，三点均在两点云的重叠区域之外了，配准效果又不好。因此需要在满足上限的基础之上，尽可能保证大的三级形面积。若没有给定点云重叠率f，则可以进行f=1.0,0.75,0.5...重叠率递减测试，选择最优变换。

step2：确定三点后，源点云四点集中第四点的选择方式为：遍历源点云中所有的点，对每一个点进行计算验证选择最优的第四点。第四点需要与其他三点组成的平面尽可能的共面（即不强制要求四点共面，但第四点到其他三点平面的距离尽可能小），并且第四点与其他三点的距离也要满足距离阈值范围（不能太近不能太远）。

step3：源点云中的四点集选择完成后，就可以计算其四点构成的两线段交点的变换不变比，根据不变比在目标点云中遍历搜索对应的满足该约束所有四点集（即下文的4PCS算法），这就是（近似）全等四点集。

4PCS算法

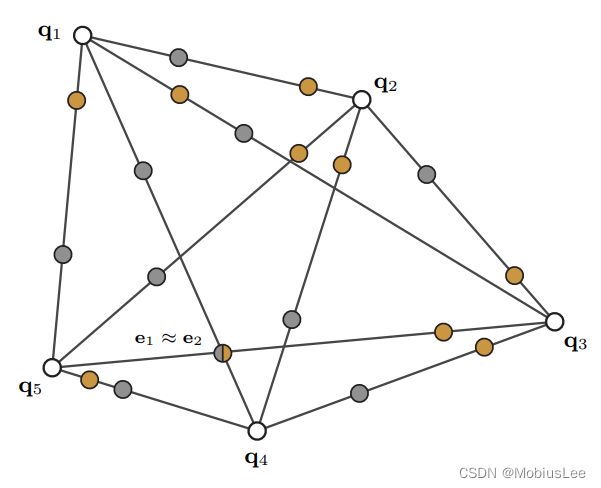
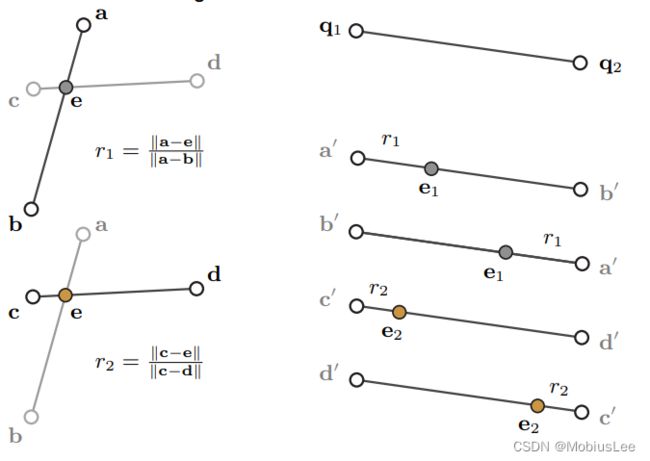
 上图中：提取仿射不变性全等四点集，（左边）给了一个基底B = {a, b, c, d} 由四个近似共面点组成，我们提取两个比率r1和r2。（中间）对任意点对{q1, q2}，可以有两个配准，一个对应于{a，b}，一个对应于{c, d}，导致四个可能的中间点。这些点计算为e1 = q1 + r1(q2−q1)和e2 = q1 +r2(q2−q1)。（右边）现在，给定一组共面点Q，我们想要提取出一个4点集合它在仿射变换中与给定的基底B全等。对于每一对点{q1, q2}∈Q，我们按所述计算四个中间点。为了简单起见，我们只在图中表示每个点对的两个点，如果e1≈e2, 4点集则约全等于给定的B。在这个例子中，{a, b, c, d}近似全等于{q5, q3, q4, q1}。

详细步骤：

step1：在源点云P中，使用上述的四点集的选择方法随机选择一个四点集B={b1,b2,b3,b4}，其中(b1,b2)确定线段1，(b3,b4)确定线段2。接着去计算不变量d1=|b1-b2|，d2=|b3-b4|（约束1），不变比r1=|b1-e| / |b1-b2|，r2=|b3-e| / |b3-b4|（约束2）。注意因为四点不一定共面，两条线段也不一定相交，所以可以使用连接两个线段的最近点的中心点作为“交点”。

step2：在目标点云Q中，遍历所有的点对，筛选满足约束1（允许有一定的误差）的点对集合R1，R2。其表示为：

计算R1 ={ (pi, pj) | pi, pj ∈ Q) }，使|| pi - pj ||∈ [ d1- δ,d1+δ ].

计算R2 ={ (pi, pj) | pi, pj ∈ Q) }，使|| pi - pj ||∈ [ d2- δ,d2+δ ].

step3: 遍历点对集合R1中的所有点对元素，计算其线段上满足不变比r1的目标交点，然后将所有计算结果e存入搜索树ANN Tree（近似最邻近搜索树，最常见的是K-D Tree算法），并构建相应的映射 

step4:遍历点对集合R2中的所有点对元素，计算其线段上满足不变比r2的目标交点，并构建相应的映射。然后遍历所有的点，在之前构建的ANN Tree中搜索可接受误差范围内的重合点，若可找到则说明能在Q中找到一个对应的近似全等四点集。最终求得所有的近似全等四点集

step5:遍历所有的近似全等四点集，对每一个，通过最小二乘法计算其与B的对应变换矩阵。然后使用该变换矩阵对源点云P进行变换得到P'，统计P'与Q中的最大公共点集（LCP），记max(LCP)的变换矩阵为本次迭代的最优变换矩阵T并保留

step6:不断迭代这个过程，记录最优的变换。迭代结束后得到的变换矩阵即为最优变换矩阵。

算法步骤伪码（原文）:

 原论文：​​​​​​4-points congruent sets for robust pairwise surface registration | ACM Transactions on Graphics​​​​​​4-points congruent sets for robust pairwise surface registration | ACM Transactions on Graphics

参考文章：点云配准（三） 传统点云配准算法概述_阿阿阿安的博客-CSDN博客_点云配准​​​​​​​​​​​