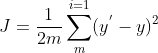机器学习-线性回归（Linear Regression）

目录

1.什么是线性回归

2. 能够解决什么样的问题

3. 一般表达式是什么

4. 如何计算

4.1 Loss Function--MSE

4.2 标准方程方法

5. 过拟合问题如何解决

5.1 什么是L2正则化(岭回归)

5.2 什么场景下用L2正则化

5.3 什么是L1正则化(Lasso回归)

5.4 什么场景下使用L1正则化

5.5 什么是ElasticNet回归

5.6 ElasticNet回归的使用场景

6. 线性回归要求因变量服从正态分布？

7. 实现代码

---

​​​​​​​

1.什么是线性回归

• 线性：两个变量之间的关系是一次函数关系的——图象是直线，叫做线性。
• 非线性：两个变量之间的关系不是一次函数关系的——图象不是直线，叫做非线性。
• 回归：人们在测量事物的时候因为客观条件所限，求得的都是测量值，而不是事物真实的值，为了能够得到真实值，无限次的进行测量，最后通过这些测量数据计算回归到真实值，这就是回归的由来。

2. 能够解决什么样的问题

对大量的观测数据进行处理，从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在，从而就可以模拟出结果，也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。例如：对房价的预测、判断信用评价、电影票房预估等。

3. 一般表达式是什么

w叫做x的系数，b叫做偏置项。

4. 如何计算

4.1 Loss Function--MSE

利用梯度下降法找到最小值点，也就是最小误差，最后把 w 和 b 给求出来。

4.2 标准方程方法

可以利用Python进行矩阵运算直接求解，也可以使用sk-learn进行求解

5. 过拟合问题如何解决

使用正则化项，也就是给loss function加上一个参数项，正则化项有L1正则化、L2正则化、ElasticNet。加入这个正则化项好处：

• 控制参数幅度，不让模型“无法无天”。
• 限制参数搜索空间
• 解决过拟合的问题。

5.1 什么是L2正则化(岭回归)

方程：

表示上面的 loss function ，在loss function的基础上加入w参数的平方和乘以 

 ，假设：

回忆以前学过的单位元的方程：

正和L2正则化项一样，此时我们的任务变成在L约束下求出J取最小值的解。求解J0的过程可以画出等值线。同时L2正则化的函数L也可以在w1w2的二维平面上画出来。如下图：

L表示为图中的黑色圆形，随着梯度下降法的不断逼近，与圆第一次产生交点，而这个交点很难出现在坐标轴上。这就说明了L2正则化不容易得到稀疏矩阵，同时为了求出损失函数的最小值，使得w1和w2无限接近于0，达到防止过拟合的问题。

5.2 什么场景下用L2正则化

只要数据线性相关，用LinearRegression拟合的不是很好，需要正则化，可以考虑使用岭回归(L2), 如果输入特征的维度很高,而且是稀疏线性关系的话， 岭回归就不太合适,考虑使用Lasso回归。

5.3 什么是L1正则化(Lasso回归)

L1正则化与L2正则化的区别在于惩罚项的不同：

求解J0的过程可以画出等值线。同时L1正则化的函数也可以在w1w2的二维平面上画出来。如下图：

惩罚项表示为图中的黑色棱形，随着梯度下降法的不断逼近，与棱形第一次产生交点，而这个交点很容易出现在坐标轴上。这就说明了L1正则化容易得到稀疏矩阵。

5.4 什么场景下使用L1正则化

L1正则化(Lasso回归)可以使得一些特征的系数变小,甚至还使一些绝对值较小的系数直接变为0，从而增强模型的泛化能力 。对于高的特征数据,尤其是线性关系是稀疏的，就采用L1正则化(Lasso回归),或者是要在一堆特征里面找出主要的特征，那么L1正则化(Lasso回归)更是首选了。

5.5 什么是ElasticNet回归

ElasticNet综合了L1正则化项和L2正则化项，以下是它的公式：

5.6 ElasticNet回归的使用场景

ElasticNet在我们发现用Lasso回归太过(太多特征被稀疏为0),而岭回归也正则化的不够(回归系数衰减太慢)的时候，可以考虑使用ElasticNet回归来综合，得到比较好的结果。

关于L1/L2正则化的解释，可以参考这篇文章

机器学习中正则化项L1和L2的直观理解_小平子的专栏-CSDN博客_l2正则

6. 线性回归要求因变量服从正态分布？

我们假设线性回归的噪声服从均值为0的正态分布。 当噪声符合正态分布N(0,delta^2)时，因变量则符合正态分布N(ax(i)+b,delta^2)，其中预测函数y=ax(i)+b。这个结论可以由正态分布的概率密度函数得到。也就是说当噪声符合正态分布时，其因变量必然也符合正态分布。

在用线性回归模型拟合数据之前，首先要求数据应符合或近似符合正态分布，否则得到的拟合函数不正确。

7. 实现代码

参考：https://github.com/Avik-Jain/100-Days-Of-ML-Code/blob/master/Code/Day2_Simple_Linear_Regression.md

# Step 1: Data Preprocessing

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

dataset = pd.read_csv('studentscores.csv')
X = dataset.iloc[ : ,   : 1 ].values
Y = dataset.iloc[ : , 1 ].values

from sklearn.cross_validation import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split( X, Y, test_size = 1/4, random_state = 0) 

# Step 2: Fitting Simple Linear Regression Model to the training set

 from sklearn.linear_model import LinearRegression
 regressor = LinearRegression()
 regressor = regressor.fit(X_train, Y_train)

 # Step 3: Predecting the Result

 Y_pred = regressor.predict(X_test)

 
 # Step 4: Visualization 
 ## Visualising the Training results

 plt.scatter(X_train , Y_train, color = 'red')
 plt.plot(X_train , regressor.predict(X_train), color ='blue')

 ## Visualizing the test results

 plt.scatter(X_test , Y_test, color = 'red')
 plt.plot(X_test , regressor.predict(X_test), color ='blue')

 文章内容参考：

ML-NLP/Machine Learning at master · NLP-LOVE/ML-NLP · GitHub此项目是机器学习(Machine Learning)、深度学习(Deep Learning)、NLP面试中常考到的知识点和代码实现，也是作为一个算法工程师必会的理论基础知识。 - ML-NLP/Machine Learning at master · NLP-LOVE/ML-NLPhttps://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning